Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

CveEYQh7MP

.pdf

Скачиваний:

Добавлен:

13.02.2021

Размер:

423.25 Кб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

МИНОБРНАУКИ РОССИИ

___________________________________

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

______________________________________

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ СИСТЕМЫ УПРАВЛЕНИЯ

Методические указания к курсовому проектированию

Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»

2014

УДК 621.372

Математическое моделирование системы управления: методич. указа-

ния к курсовому проектированию / сост.: О. Ю. Лукомская, А. Г. Шпекторов.

СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2014. 40 с.

Содержат указания по базовым процедурам исследования и моделиро-

вания движения морских подвижных объектов на примере катера и корабля на подводных крыльях. Приводятся теоретические основы анализа движения подвижных объектов, а также практические рекомендации по созданию про-

граммной модели и исследованию движения морских подвижных объектов в среде MATLAB, по разработке интерфейса программы моделирования ко-

раблей разных типов с использованием элементов MATLAB GUI.

Предназначены для магистрантов, обучающихся по направлению

«Управление в технических системах», а также могут быть полезны инже-

нерно-техническим работникам этой области знаний.

Утверждено редакционно-издательским советом университета

в качестве методических указаний

Целью курсовой работы является выработка у студентов умения и практиче-

ских навыков составления и написания программных моделей для исследо-

вания в среде MATLAB, создания интерфейсов для вывода результатов мо-

делирования с использованием элементов MATLAB GUI.

Курсовая работа включает в себя следующие основные этапы:

1.Постановка задачи и формирование ее математической модели.

2.Разработка блок-схемы алгоритма решения задачи.

3.Написание и отладка программной модели движения.

4.Представление и анализ результатов работы.

СПИСОК ОБОЗНАЧЕНИЙ

GUI – Graphic User Interface;

ГЭУ – главная энергетическая установка;

КПК – корабль на подводных крыльях;

НВК – надводный водоизмещающий корабль;

ПК – персональный компьютер;

СИ – система измерений;

ТТД – тактико-технические данные.

1. ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ОБЪЕКТОВ УПРАВЛЕНИЯ

1.1. Математическая модель движения надводного водоизмещающего корабля

В наиболее общем виде поступательное движение любого объекта, в

данном случае надводного водоизмещающего корабля, можно описать с по-

мощью второго закона Ньютона:

ma = F − R ,

(1.1)

где m, a – масса корабля и его ускорение.

Правая часть представляет собой алгебраическую (с учетом направле-

ния, знака) сумму сил, действующих на корабль (рис. 1.1). Для НВК будем рассматривать следующие силы: F – движущая сила, или сила тяги винта

(движителя), Н; R – сила сопротивления движению, Н.

Уравнение (1.1) называют также балансным уравнением движения ко-

рабля. При балансе или равенстве сил F и R ускорение корабля равно нулю,

корабль движется равномерно (с постоянной скоростью) и прямолинейно.

Если F > R – корабль разгоняется, и наоборот.

Сила сопротивления направлена в сторону, противоположную силе тя-

ги, и зависит от многих параметров движения, геометрии корпуса НВК и внешних возмущений [1]. Однако в первом приближении ее можно считать

пропорциональной квадрату скорости корабля: R = Av 2 , или для возможно-

сти учета направления

R = Av		v		,	(1.2)

где А – коэффициент пропорциональности.

R, Н

F, Н

x, м

Рис. 1.1. Схема сил, действующих на надводный водоизмещающий корабль при прямолинейном движении

Такой подход является приближенным и годится лишь для построения упрощенных моделей. С учетом формулы (1.2) балансное уравнение движе-

ния (1.1) теперь может быть записано следующим образом:

ma = F − Av		v		.	(1.3)

Входящая в уравнение (1.3) скорость в некоторый момент времени ti

(мгновенная скорость) в направлении координаты пройденного расстояния x

(рис. 1.1) в общем случае определяется как v = dx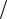dt .

Коэффициент пропорциональности силы сопротивления движению А мо-

жет быть определен по граничным условиям, известным для каждого модели-

руемого объекта, максимальному значению скорости vmax при максимальной силе тяги Fmax . Поскольку скорость vmax ограничена силой сопротивления

среды, т. е. F	= R	, то можно записать F			= Av	2	, откуда
max	max			max		max
		A =	Fmax	.			(1.4)
		A =		.			(1.4)
			vmax2

Ограничения разработанной модели:

1.Предполагается, что корабль движется на постоянном курсе.

2.Не учитывается волнение моря, гидродинамические особенности корпуса, переменное воздействие ветра и т. п.

Сила тяги, определяемая оборотами винтов судна, не может изменяться мгновенно вследствие инерционности вращающих винт двигателей. Полагая зависимость силы тяги от времени линейной, ее изменение можно также описать при помощи дифференциального уравнения с нелинейностью типа

«ограничение» («насыщение»):

			dF	= kF ;		F	≤ F *,		(1.5)
			dF

			dt					* , F* ≤ F
где k	F	– коэффициент скорости изменения тяги, Н/с; F						* , F* ≤ F	– заданное
	F							max
значение силы тяги. Коэффициент k F					– постоянный по модулю,				но может

иметь разные знаки (для моделирования разгона и торможения НВК).

При известном начальном значении силы тяги можно решить дифферен-

циальное уравнение (1.5) и задавать в модели силу тяги как функцию времени.

Для придания математической модели (ММ) универсальности целесо-

образно, по возможности, использовать не абсолютные величины, а их отно-

сительные значения. В данном случае предпочтительно принять относитель-

ные значения силы тяги в процентах от максимальной:

F * =

P*F

max

(1.6)

100

где P* – относительное значение силы тяги в процентах от максимальной.

Соответственно, имеем модель НВК:

= v;

[F (t ) − A

v];

dt m

(1.7)

A =

Fmax

;

vmax2

F (t ) =

P(t )Fmax

100

Полученная математическая модель (1.7) позволяет для любого мо-

мента времени определить расстояние, пройденное кораблем (координата

x(t )), и скорость движения v(t ) по задаваемым значениям силы тяги P* . Пе-

реход к относительным величинам позволяет вводить в качестве исходных дан-

ных значения силы тяги (мощности двигателя) в процентах от максимальной, а

не в ньютонах, как и принято в современной практике судовождения.

Математическая модель (1.7) может быть использована для изучения динамических характеристик корабля при проектировании, эксплуатации,

создании тренажеров и т. п.

1.2. Математическая модель движения корабля на подводных крыльях

Скорость движения кораблей на подводных крыльях в два-три раза выше скорости водоизмещающих кораблей и может достигать 65 узлов

(≈120 км/ч). Это предельная скорость для КПК из-за кавитации, возникающей на крыльях и лопастях винта.

Особенностью движения корабля на подводных крыльях, в отличие от водоизмещающего надводного корабля, является наличие трех режимов движения:

–движение на корпусе (водоизмещающий режим). Осуществляется до определенной скорости vk , после чего переходит в режим глиссирования;

–глиссирование – режим движения, когда корабль, набрав скорость vk ,

начинает выходить из воды на крылья, достигая при этом скорости v1max , после которой переходит в следующий режим;

– движение на крыльях (крыльевой режим); при достижении скорости v1max на крыльях возникает и поддерживается соответствующая подъемная сила, сопротивление среды резко уменьшается, а максимально возможная скорость v2 max увеличивается.

Указанная особенность режима движения на крыльях должна быть учтена при разработке математической модели. При моделировании движения водоизмещающего корабля было показано, что сила сопротивления движению пропорциональна квадрату скорости (1.2). Для корабля на подводных крыльях существует два коэффициента пропорциональности:

A1 – при v £ vk (водоизмещающий режим);

A2 – при v ³ vk (режим глиссирования и движения на крыльях), что обес-

печивает возможность достижения максимальных скоростей v1max и v2 max .

Таким образом, математическая модель КПК имеет вид

= v;

[F (t ) - A

v];

Fmax

, v < vk ;

(1.8)

v1max

A =

Fmax

,v ³ vk ;

2max

F (t ) = P(t )Fmax .

100

1.3. Уточнение математических моделей

Одним из методов построения математической и реализующей ее на компьютере программной моделей является метод «быстрого прототипа».

Основное содержание его заключается в том, что вначале строится максимально упрощенная математическая модель с целью получить первые результаты ис-

следования и оценить их правдоподобность в максимально короткие сроки, т. е.

проверяется перспективность выбранного направления исследований.

В дальнейшем ММ постепенно усложняется и уточняется с целью все больше-

го приближения выходных данных к реальным.

В математической модели (1.8), например, показано, что коэффициент силы сопротивления движению А принимает значения A2 при v ³ vk , т. е.

подчиняется релейному закону (рис. 1.2, а). В первом приближении это со-

ответствует действительности. Однако в реальных условиях сила не может измениться скачком, вследствие чего корабль выходит в крыльевой режим не мгновенно, а в течение некоторого времени. Естественно, что сила сопро-

тивления, выражаемая коэффициентом А, уменьшается постепенно, по мере выхода корпуса из воды на крылья. При скорости v1max значение коэффици-

ента А действительно становится равным A2 .

Режим глиссирования корабля на подводных крыльях является пере-

ходным и кратковременным, и, вообще говоря, сопротивление на корпусе в этом режиме не может быть определено по формуле (1.4), поскольку она справедлива для установившегося движения.

A					Очевидно,	что принятый релей-
A					ный закон смены коэффициентов не-
A1					ный закон смены коэффициентов не-
A1					достаточно точен. Для устранения
					достаточно точен. Для устранения
					недостатка можно принять, напри-
A2					мер линейный закон изменения ко-
					эффициента А в зависимости от ско-
v		v1		v	рости корабля (рис. 1.2,		б). Это при-
k	a		max
	a		max		близит модель к реальному объекту.
A					близит модель к реальному объекту.
A1					Вероятно, этот	закон	не является
A1
					строго линейным и для дальнейшего
					уточнения модели требуются допол-
A2					нительные аналитические исследова-
					ния или натурные испытания. Про-
vk	б	v1max		v	цесс уточнения	математической мо-
	б

Рис. 1.2. Законы изменения коэффициента А: дели носит последовательный итера-

а – релейный; б – линейный

ционный характер.

Для принятого линейного закона коэффициент А будет определяться из

следующей системы уравнений:

A = A1,

v ≤ vk ;

A = A -

(v - vk )(A1 - A2 )

, v

£ v £ v

;

- vk

1max

max

A = A2 ,

v ³ v1

;

(1.9)

max

A =

Fmax

, v £ v

;

1max

A =

Fmax

, v ³ v

2max

2. ФОРМИРОВАНИЕ ПРОГРАММНЫХ МОДЕЛЕЙ

Компьютерная программа, реализующая полученную математическую модель, обычно носит название программной модели. Создание программной модели является следующим этапом моделирования на ПК.

Современные программные средства позволяют моделировать динами-

ческие системы в непрерывном времени. Программная среда MATLAB име-

ет достаточно мощный аппарат для численного интегрирования и аналити-

ческого решения дифференциальных уравнений. Одной из многих функций численного интегрирования является функция ode45, имеющая следующий базовый формат записи:

[TOUT,YOUT] = ode45(ODEFUN,TSPAN,Y0).

Здесь ODEFUN – имя функции, вычисляющей правую часть дифферен-

циального уравнения; TSPAN – вектор, определяющий начальное и конеч-

ное значения временного интервала, на котором осуществляется интегриро-

вание; Y0 – вектор начальных условий; TOUT – вектор моментов времени,

для которого получены матрицы частного решения YOUT.

Альтернативным способом численного моделирования нелинейных дина-

мических систем является переход к разностным уравнениям. При этом про-

граммные модели могут быть сформированы без применения специализиро-

ванных функций на любом высокоуровневом языке программирования. Урав-

нения решают последовательно для дискретных моделей времени ti , ti+1 , ... .

При этом ti+1 = ti + t ,

где

t = const

–

шаг приращения времени (интегри-

рования). Таким образом, при выборе достаточно малого шага

t мгновенная

скорость может быть определена по конечной разности расстояний:

(xi − xi−1 )

(2.1)

а ускорение в момент времени ti+1 = ti

– по формуле

ai+1 = (vi+1 − vi )

t = (

xi+1

t −

t )

t = (

xi+1 −

xi )

t2 . (2.2)

Подставив формулы (2.1) и (2.2) в уравнение движения (1.3), получим:

m(x

− x

−

x )

t 2 = F

− A

t 2

(2.3)

i +1

откуда легко получить расчетную рекуррентную формулу для вычисления очередного значения координаты пройденного расстояния:

xi +1 = xi + xi + (Fi t − A xi		xi		) m .	(2.4)

Из уравнений (2.3) и (2.4) видно, что для вычисления скорости движе-

ния НВК необходимо иметь значения двух координат ( xi−1 и xi ), в то время как для определения ускорения – три, дополнительно xi+1 .

В окончательном виде математическая модель движения надводного водо-

измещающего корабля (1.7) может быть представлена системой уравнений:

				(P F	Dt	2 100 - A Dx	Dx	)
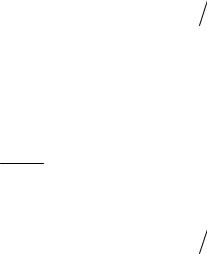
				(P F	Dt	2 100 - A Dx	Dx	)
x	= x + Dx	i	+	i max		i	i		;
				i max		i	i

i +1	i					m
	= Dxi +1 = (xi +1 - xi )					m
v	= Dxi +1 = (xi +1 - xi )				;
i +1	Dti			Dt
	Dti			Dt

Dxi = xi - xi −1;

A = F2max ,

vmax

а математическая модель движения КПК (1.8)

(P F

2 100 - A Dx

)

= x + Dx

i max

;

i +1

= Dxi +1 = (xi +1 - xi )

;

i +1

Dti

Dxi = xi - xi −1;

A =

Fmax

;

£ v

;

i +1

1max

A =

Fmax

;

³ v

i +1

2max

(2.5)

(2.6)

где Pi – относительное значения силы тяги в процентах от максимальной.

Математическая модель (2.6) также может быть уточнена в соответ-

ствии с (1.9).

Достоинством использования функции ode45 является встроенный вы-

бор шага интегрирования. В расширенном формате записи функции ode45

можно задавать другие параметры моделирования, в том числе и диапазон изменения шага интегрирования.

2.1. Выбор шага интегрирования

Так как при моделировании на ПК уравнения решают последовательно для определенных (дискретных) значений времени, то для обеспечения тре-

буемой точности достаточно важен выбор шага приращения времени Dt.

Известно, что при выборе неоправданно большого шага численные ме-

тоды интегрирования могут «разойтись», т. е. привести к неограниченному росту вычисляемых переменных. Слишком малый шаг интегрирования при-

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.02.2021296.84 Кб168T5nqUMP4D.pdf
#
13.02.2021236.08 Кб094qX9psXqs.pdf
#
13.02.2021993.47 Кб2AseGu7p6By.pdf
#
13.02.2021561.29 Кб1caO76D6RYL.pdf
#
13.02.2021391.66 Кб1cULCTvlN06.pdf
#
13.02.2021423.25 Кб1CveEYQh7MP.pdf
#
13.02.2021502.93 Кб4DPbX1BcL8t.pdf
#
13.02.2021401.97 Кб1E3W3aEqN89.pdf
#
13.02.2021241.27 Кб4EjgIU2M2vi.pdf
#
13.02.2021267.4 Кб3ERBI7HWOco.pdf
#
13.02.2021414.88 Кб3ezM0YUQ7Uv.pdf