
Kxp751v5RS
.pdfМИНОБРНАУКИ РОССИИ
____________________________________
Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»
______________________________________
АДАПТИВНЫЕ ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ
Методические указания к лабораторным работам
Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»
2014
УДК 519.24:62
Адаптивные измерительные системы: методич. указания к лаб. работам / сост.: Б. Я. Авдеев, А. А. Минина. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2014. 24 с.
Дано описание лабораторных работ по одноименной дисциплине, представлены методы дискретного представления сигналов в адаптивных измерительных системах, вопросы формирования и анализа адаптивной временной дискретизации сигналов.
Предназначены для подготовки магистров по направлению 200100.68 «Приборостроение», магистерским программам 200147.68 «Адаптивные измерительные системы» и 200146.68 «Локальные измерительно-вычислительные системы», а также могут быть использованы при реализации программ дополнительного образования.
Утверждено редакционно-издательским советом университета
в качестве методических указаний
© СПбГЭТУ «ЛЭТИ», 2014
Методические указания включают первые базовые работы общего цикла лабораторных работ по дисциплине «Адаптивные измерительные системы», посвященные вопросам метрологического анализа равномерной временной дискретизации, а также формирования и анализа адаптивного представления сигналов в измерительных системах. Эти вопросы объединены задачами формирования измерительных сигналов, предназначенных для экспериментальных исследований тех или иных видов дискретного представления сигналов в информационно-измерительных системах.
Лабораторные работы реализованы на базе персональных компьютеров. Для выполнения работ необходимо иметь начальные знания по использованию пакета прикладных программ MatLab в задачах проведения необходимых расчетов, имитационного моделирования процессов и систем, а также представления результатов экспериментальных исследований.
Требования к отчету по лабораторным работам. Отчет должен содержать:
1.Титульный лист, оформленный в соответствии с принятой формой.
2.Задания на лабораторную работу.
3.Расчетные формулы и примеры расчетов.
4.Описание алгоритмов и распечатку программ выполненных экспериментов.
4.Результаты имитационного моделирования и расчетов.
5.Выводы по полученным результатам экспериментальных исследований.
Лабораторная работа 1.
ФОРМИРОВАНИЕ ИМИТАЦИОННЫХ МОДЕЛЕЙ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ
С ЗАДАННЫМИ ХАРАКТЕРИСТИКАМИ
Цель работы – изучение методов формирования имитационных моделей детерминированных и случайных сигналов с заданными метрологическими характеристиками в среде интерактивного программирования MatLab.
Задание
1.Формирование детерминированных сигналов с заданными метрологическими характеристиками:
1.1.Получить у преподавателя задание по формированию имитационных моделей по виду сигналов и их амплитудным, временным и точностным характеристикам представления.
3
1.2.Разработать программу, реализующую в среде программирования MatLab формирование заданных сигналов и оценку их характеристик.
1.3.Экспериментально оценить параметры сформированных моделей. Построить графики полученных моделей. Сделать вывод о соответствии параметров моделей техническому заданию.
2.Формирование некоррелированных случайных последовательностей чисел с заданными функциями распределения:
2.1.Получить у преподавателя задание по формированию имитационных моделей некоррелированных случайных последовательностей чисел с заданными функциями распределения (вид функции распределения и ее числовые параметры, объем выборки).
2.2.Разработать программу, реализующую в среде программирования MatLab формирование заданных последовательностей чисел и оценку их характеристик.
2.3.Экспериментально оценить параметры сформированных моделей. Построить графики полученных моделей. Сделать вывод о соответствии параметров моделей техническому заданию.
3.Формирование стационарных случайных гауссовых сигналов с заданными корреляционными функциями:
3.1.Получить у преподавателя задание по формированию имитационных моделей гауссовых сигналов с требуемыми корреляционной функцией и точностным характеристикам представления сигналов.
3.2.Рассчитать параметры цифрового фильтра для реализации заданной корреляционной функции.
3.3.Разработать программу, реализующую в среде программирования MatLab формирование заданных сигналов и оценку их характеристик.
3.4.Экспериментально оценить параметры сформированных моделей. Построить графики полученных моделей сигналов и корреляционных функций. Сделать вывод о соответствии параметров моделей техническому заданию.
Общие сведения и порядок выполнения работы
Формирование детерминированных измерительных сигналов с заданными характеристиками. Измерительный сигнал – это сигнал, содер-
жащий количественную информацию об измеряемой физической величине.
4
Детерминированный сигнал – это сигнал, закон изменения которого известен, а модель не содержит неизвестных параметров. В данном подразделе необходимо сформировать дискретную модель сигнала, если его вид, частота, длительность и погрешность представления или частота дискретизации заданы.
При моделировании измерительных систем широко используются де-
терминированные сигналы различной формы – синусоидальные, прямо-
угольные, экспоненциальные и т. п. В ППП MatLab формирование таких сиг-
налов не вызывает затруднений. Для измерительных задач важным является погрешность дискретного представления аналоговых сигналов.
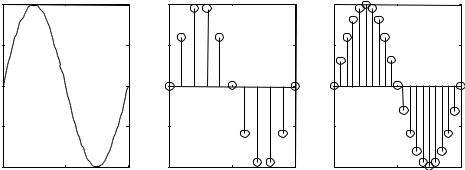
На рис. 1.1 показано формирование двух дискретных моделей исходного аналогового синусоидального сигнала x(t) = xm sin ωt (рис. 1.1, а) при его равномерной дискретизации 10-ю (рис. 1.1, б) и 20-ю (рис. 1.1, в) отсчетами сигнала на периоде Т исходной (заданной для моделирования) синусоиды.
x(t)/xm |
|
|
1 |
|
|
1 |
|
|
|
|
0.5 |
|
|
0.5 |
|
|
0.5 |
|
|
|
0 |
|
|
0 |
|
|
0 |
|
|
– |
0.5 |
|
– |
0.5 |
|
– |
0.5 |
|
|
|
– 1 |
0.5 |
t /T |
– 1 |
0.5 |
1 |
– 1 |
0.5 |
1 |
|
0 |
0 |
0 |
||||||
|
|
а |
|
|
б |
|
|
в |
|
Рис. 1.1. Формирование дискретного представления синусоидального сигнала |
|||||||||
Очевидно, что во втором случае дискретная модель более точно воспро-
изводит исходный сигнал. Погрешность воспроизведения определяется не только частотой дискретизации, но и для многих задач видом аппроксимации исходного сигнала по его дискретным отсчетам. Аналитические соотноше-
ния, связывающие погрешности аппроксимации сигнала и частоту (интервал)
его дискретного представления, даны в [1], [2], а также в лаб. раб. 2.
Таким образом, при моделировании сигналов исходным требованием к модели может быть как частота дискретизации, так и погрешность ап-
проксимации сигнала при заданном виде представления его на интервалах дискретизации.
5

Формирование случайных измерительных сигналов с заданными характеристиками. Случайный сигнал – это изменяющаяся во времени физическая величина, мгновенное значение которой является случайной величиной.
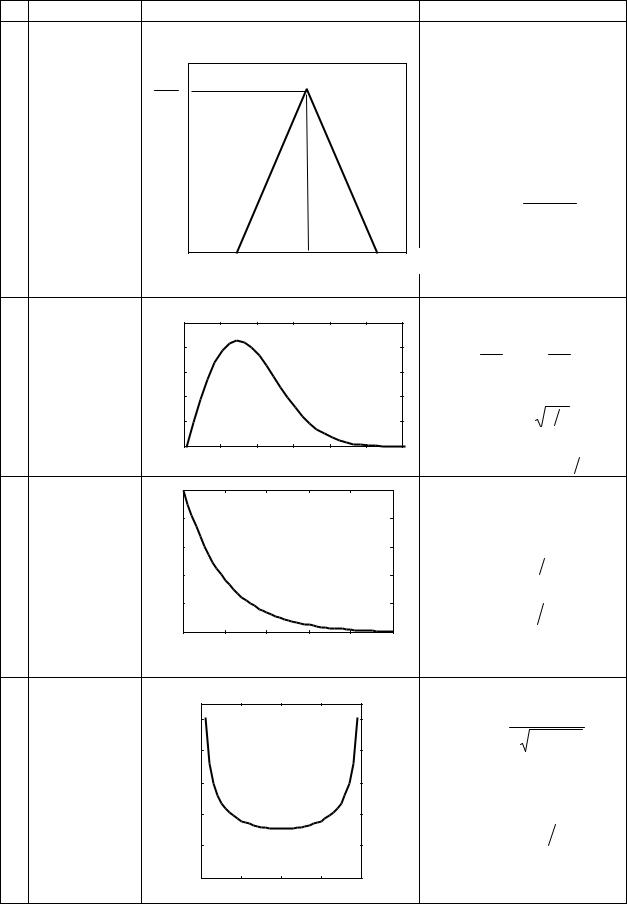
В табл. 1.1 приведены наиболее распространенные законы распределения (ЗР) случайных величин: равномерный, нормальный, Симпсона, Рэлея, экспоненциальный, арксинуса.
Функции для реализации задания на лабораторную работу в ППП
MatLab приведены в табл. 1.2.
|
|
|
|
|
|
|
|
|
Таблица 1.1 |
|
|
|
|
|
|
|
|
|
|
№ |
Название |
|
|
|
|
График |
|
Формулы |
|
|
|
|
|
|
|
|
|
|
|
1 |
Равномерный |
|
|
|
|
|
|
|
X = a + γ(b − a) , |
|
ЗР |
W(x) |
|
|
|
|
|
где a и b – границы рав- |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
номерного ЗР; γ – случай- |
|
|
1 |
|
|
|
|
|
|
ная величина, распределен- |
|
|
b − a |
|
|
|
|
|
|
ная по равномерному ЗР в |
|
|
|
|
|
|
|
|
|
диапазоне [0,1]. |
|
|
|
|
|
|
|
|
|
Математическое ожидание: |
|
|
|
|
|
|
|
|
|
m[ X ] = (a + b) 2 , |
|
|
|
|
|
|
|
|
|
дисперсия: |
|
|
|
|
|
|
|
|
|
D[ X ] = (b − a)2 12 |
|
|
0 |
|
|
|
|
|
|
|
|
|
a |
b |
x |
|||||
|
|
|
|
||||||
2 |
Нормальный |
|
|
|
|
|
|
Плотность распределения: |
|
|||||
|
ЗР |
W(x) |
|
|
|
|
|
W (x) = |
|
1 |
|
(x − m) |
2 |
|
|
|
|
|
|
|
|
|
|
exp − |
. |
||||
|
|
|
|
|
|
|
|
|
σ |
2π |
|
2σ |
2 |
|
|
|
0,3 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Математическое ожидание: |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
0,2 |
|
|
|
|
|
|
|
m[ X ] = m , |
|
|
||
|
|
|
|
|
|
|
дисперсия: |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0,1 |
|
|
m = 3 |
|
|
|
|
D[ X ] = σ2 |
|
|
|
|
|
|
|
|
σ = 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,0 |
1 |
2 |
3 |
4 |
5 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6
|
|
|
|
|
|
|
|
|
|
Окончание табл. 1.1 |
||||||
№ |
Название |
|
|
|
График |
|
|
|
Формулы |
|
|
|||||
3 |
Распределение |
|
|
|
|
|
|
|
Распределение |
|
Симпсона |
|||||
|
Симпсона |
W(x) |
|
|
|
|
|
|
можно получить, как сумму |
|||||||
|
|
1 |
|
|
|
|
|
|
двух равномерных ЗР: |
|||||||
|
|
b−a |
|
|
|
|
|
|
|
X = X1 + X 2 . |
|
|||||
|
|
|
|
|
|
|
|
|
Математическое ожидание: |
|||||||
|
|
|
|
|
|
|
|
|
|
m[ X ] = a + b , |
|
|||||
|
|
|
|
|
|
|
|
|
дисперсия: |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
D[ X ] = |
(b - a)2 |
||||||
|
|
|
|
|
|
|
|
|
|
6 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2a |
|
a + b |
2b |
x |
|
|
|
|
|
|
|
|
4 |
Распределение |
W(x) |
|
|
|
|
|
|
Плотность распределения: |
|||||||
|
Рэлея |
|
|
|
|
|
|
|
x |
|
|
x |
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
0.4 |
|
|
|
s = 1 |
|
|
W (x) = |
|
- |
2 |
|
|||
|
|
0.3 |
|
|
|
|
|
s |
2 exp |
s |
, x ³ 0. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0.2 |
|
|
|
|
|
|
Математическое ожидание: |
|||||||
|
|
|
|
|
|
|
|
m[ X ] = s |
p 2 , |
|||||||
|
|
0.1 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
дисперсия: |
|
|
|
|
|
|||
|
|
0.0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
2 |
|
x |
D[ X ] = s2 (4 - p) 2 |
||||||||
|
|
|
|
|
|
|||||||||||
5 |
Экспоненци- |
W(x) |
|
|
|
|
|
|
Плотность распределения: |
|||||||
|
альный ЗР |
0.8 |
|
l = 1 |
|
|
|
W (x) = l exp(-lx), |
x ³ 0. |
|||||||
|
|
0.6 |
|
|
|
|
Математическое ожидание: |
|||||||||
|
|
|
|
|
|
|
|
|
m[x] = 1 l, |
|
||||||
|
|
0.4 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
дисперсия: |
|
|
|
|
|
|||
|
|
0.2 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
D[x] = 1 l2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
0 |
1 |
|
2 |
3 |
4 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
6 |
ЗР арксинуса |
W(x) |
|
|
|
|
|
|
Плотность распределения: |
|||||||
|
|
|
|
|
|
|
|
W (x) = |
|
1 |
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0.4 |
|
|
a = 2 |
|
|
|
|
|
p |
a 2 + x 2 |
||||
|
|
|
|
|
|
|
|
Математическое ожидание: |
||||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
0.3 |
|
|
|
|
|
|
|
|
m[x] = 0 , |
|
|
|||
|
|
0.2 |
|
|
|
|
|
|
дисперсия: |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
D[x] = a 2 |
|
|
|
||||
|
|
0.1 |
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
– 1 |
0 |
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
– 2 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.2 |
|
|
|
|
|
№ |
Название |
Описание функции для реализации в MatLab |
|
1 |
Равномерный |
X = rand(m, n) формирует массив размером m × n, элементами |
|
|
ЗР |
которого являются случайные величины, распределенные по рав- |
|
|
|
номерному закону в интервале (0, 1). |
|
|
|
f = unifpdf(x, a, b) служит для расчета значения функции плотности |
|
|
|
вероятности равномерного распределения для параметров a, b и |
|
|
|
значения Х |
|
2 |
Нормальный |
X = randn(m, n) формирует массив размером m × n, элементами |
|
|
ЗР |
которого являются случайные величины, распределенные по |
|
|
|
нормальному закону с математическим ожиданием 0 и средне- |
|
|
|
квадратическим отклонением 1. |
|
|
|
f = normpdf(X, MU, SIGMA) служит для расчета значений функции |
|
|
|
плотности вероятности нормального распределения для значений |
|
|
|
случайной величины Х, математического ожидания MU и средне- |
|
|
|
квадратического отклонения SIGMA. Размерность векторов или |
|
|
|
матриц X, MU, SIGMA должна быть одинаковой |
|
3 |
Распределение |
Может быть получен как сумма двух равномерных ЗР |
|
|
Симпсона |
|
|
4 |
Распределение |
R = raylrnd(B, m) позволяет получить вектор псевдослучайных чи- |
|
|
Рэлея |
сел на m элементов, распределенных по закону Рэлея для параметра |
|
|
|
B, где m – вектор размерностью 1 × 2, определяющий размерность |
|
|
|
матрицы R |
|
5 |
Экспоненцаль- |
X = exprnd – генератор случайных чисел, имеющих экспоненци- |
|
|
ный ЗР |
альное распределение; |
|
|
|
f = exppdf(x, mu) – служит для расчета значения функции плотности |
|
|
|
вероятности экспоненциального распределения |
|
6 |
ЗР арксинуса |
X=sin(2*pi*R) – может быть получен на основе равномерного ЗР. |
|
|
|
В приведенной записи R – случайные числа, распределенные |
|
|
|
равномерно |
|
7 |
Для всех ЗР |
[f, xi] = ksdensity(X) – функция предназначена для расчета значе- |
|
|
|
ний функции распределения плотности вероятностей f для значе- |
|
|
|
ний случайной величины xi; |
|
|
|
cdfplot(X) – функция предназначена для построения графика |
|
|
|
функции распределения СВ Х |
|
Моделирование стационарного случайного процесса методом сколь-
зящего суммирования. Для стационарных случайных процессов существуют весьма экономичные моделирующие алгоритмы. В основу этих алгорит-
мов положено линейное преобразование последовательности x[n] независи-
мых нормальных случайных чисел (дискретный белый шум) в последова-
тельность ξ[n] , коррелированную по заданному закону. Используется метод скользящего суммирования [3]
8
p |
|
x[n] = ∑Ck x[n - k ] , |
(1.1) |
− p |
|
где p – половина окна скользящего суммирования; n – текущая координата;
k – текущая координата скользящего окна; Ck – весовые коэффициенты, ко-
торые находятся по формуле в зависимости от корреляционной функции. Полученная последовательность является статистически связанной, т. е. каждое число в последовательности может находиться в определенном диапазоне относительно предыдущего. Другими словами, корреляционная функция определяет условную дисперсию реализации следующих чисел по отношению к текущим (статистическую связь) в общей последовательности значений моделируемого процесса.
При выполнении лабораторной работы будем считать, что для заданной последовательности независимых случайных величин x[n] с нулевым мате-
матическим ожиданием и нулевой дисперсией (ортонормированная последовательность случайных величин или нормированный дискретный белый шум) корреляционная функция последовательности имеет вид
R[n] = M{x[k] x[k + n]} = d = 1, n = 0, |
|
n |
{ 0, n ¹ 0. |
|
|
Сформируем из последовательности x[n] согласно алгоритму (1.1) но- |
|
вую последовательность ξ[n] : |
|
ξ[n] = C1x[n − 1] + ... + CN x[n − N ] , ξ[n + 1] = C1x[n] + ... + CN x[n + 1 − N ].
Случайная величина ξ[n] получается суммированием (с весами C1, C N )
N независимых случайных чисел, представляющих собой отрезок последо-
вательности x[n] . При этом для вычисления очередного значения ξ[n + 1]
исходная последовательность x[n] сдвигается на один элемент вправо, так что значение x[n − N ] выбрасывается. Коррелированность между случайны-
ми величинами ξ[n] и ξ[n + 1] обеспечивается за счет того, что в их образо-
вании участвует k общих случайных величин последовательности x[n]. При k = n значения ξ[n] и ξ[n + k ] становятся некоррелированными. Характер корреляционных связей процесса определяется лишь выбором значений коэффициентов Ck и не зависит от закона распределения исходных случайных
9

чисел x[n]. Если исходные случайные числа распределены нормально, то в силу линейности преобразования последовательность ξ[n] будет нормаль-
ным случайным процессом.
Таким образом, методом скользящего суммирования можно формировать дискретные реализации стационарных нормальных случайных процессов с ограниченной во времени корреляционной функцией, определяемой выбором.
Для создания коррелированной последовательности ξ[n] с корреляци-
онной функцией R(τ) = σ2 sin w0τ используется моделирующий алгоритм (1.1). |
|||
w τ |
|
|
|
0 |
|
|
|
При этом весовые коэффициенты вычисляются по формуле [3] |
|
||
Ck = |
σ |
sin γ0k , |
(1.2) |
|
πγ0 |
k |
|
где γ0 ≤ π, γ0 = w0 t .
Данный алгоритм является приближенным, однако при увеличении па-
раметра p методическая погрешность может быть сделана пренебрежимо малой.
|
ξ(n) |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
|
|
|
|
|
– |
1 |
|
|
|
|
|
– |
2 |
|
|
|
|
|
– |
3 |
|
1 000 |
|
2 000 |
|
|
0 |
|
|
||
R(n) |
|
|
|
|
||
|
0.8 |
|
|
|
|
|
|
0.4 |
|
|
|
|
|
|
0.0 |
|
|
|
|
|
– |
0.4 |
|
|
|
|
|
|
|
0 |
50 |
100 |
150 |
n |
|
|
|
|
б |
|
|
3 000 |
4 000 |
n |
а |
|
|
N(ξi) |
|
|
15 000 |
|
|
10 000 |
|
|
5 000 |
|
|
0 |
|
ξi |
– 3 – 2 – 1 0 1 2 3 |
||
|
в |
|
Рис. 1.2. Фрагмент реализации корреляционной последовательности и выборочные оценки корреляционной функции и гистограммы распределений
10
