Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4607 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Томский Государственный Университет Систем Управления и Радиоэлектроники
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

1754

.pdf
Скачиваний:
7
Добавлен:
13.02.2021
Размер:
3.58 Mб
Скачать
☆

151

Условную плотность вероятности х находим по формуле

(1.4)

W x y

W y x W x

W y

 

 

 

 

 

 

 

 

 

 

y x 2

 

 

2

 

 

2

 

 

 

 

2

 

y

 

exp

1

 

x mx

 

y mx

.

 

 

 

 

 

 

 

2

2

2

 

2

 

 

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

v

x

 

v

 

x

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В выражении, стоящем под знаком экспоненты, осуществляем возведение в квадрат и затем группируем члены, содержащие х2 и х. В итоге убеждаемся, что условное распределение величины х также нормально

 

 

 

 

 

x S

 

y

2

 

W x y

1

 

exp

 

 

,

 

 

 

 

 

 

 

 

 

 

2

2

 

 

2

 

 

 

 

 

 

 

2

где S y m x x y m x – условное математическое

2 y

ожидание X,

 

2

 

2

 

2

x

 

v

- условная дисперсия X.

 

 

2

 

 

 

 

 

y

Для ответа на вопрос п. а) следует по формуле (3.1.2) вычислить величину средней взаимной информации между ансамблем X и реализацией у

I X ; y M ln W X y W X

 

 

 

X S

y

2

 

X

m

 

2

 

M ln

x

 

 

 

x

.

 

 

 

 

 

 

 

 

 

2

2

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

Находим квадраты разностей и выносим за знак математического ожидания слагаемые и множители, не зависящие от х. Далее учитываем, что вычисляются условные математические ожидания при конкретном значении у, поэтому

152

M X S y , M X 2

 

S 2 y

2 .

В итоге получаем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

2

 

 

 

 

1

 

 

 

1

 

 

 

 

 

y

mx

 

 

I X ; y

ln

 

y

 

 

x

 

 

1

2

2

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

v

 

 

y

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

ln

104

 

 

100

 

 

 

 

y

220 2

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2 104

 

 

 

104

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

1,629

0, 4801

 

 

 

y

220 2

1

нат.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

104

 

 

 

 

Таким образом, искомая зависимость есть параболическая функция разности y m x , причем наименьшее количество информации, равное 1,1482 нат, доставляет наиболее вероятное показание прибора y m x 220 В .

Для ответа на вопрос п. б) необходимо найти среднюю величину взаимной информации между ансамблями X и Y. Вычисляем безусловное математическое ожидание величины I(Х; у).

При этом учитываем, что M Y

m

2

 

2

, и получаем

 

 

 

 

 

 

 

x

 

y

 

 

1

 

2

 

1

 

 

 

2

 

 

I X ;Y

ln

y

ln

1

 

x

1,629 нат.

2

2

2

 

2

 

 

 

 

 

 

 

 

 

v

 

 

 

v

 

 

 

 

 

 

 

 

 

 

 

 

Обратите внимание, что в среднем количество получаемой информации в данном примере зависит только от отношения

«сигнал/ошибка» x 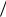v .

Пример 6.2. Для контроля исправности блока периодически измеряют значение напряжения в контрольной точке схемы. Если блок исправен, то это напряжение равно 1 В, в противном случае – 0 В. Ошибка вольтметра распределена равномерно с нулевым математическим ожиданием, но ширина этого распределения зависит от величины измеряемого напряжения: она равна 2 В, если напряжение на входе 1 В, и 1 В – в противном случае. В среднем в 90% времени блок исправен.

153

Найти количество информации, доставляемой прибором при одном измерении.

Решение. Введем обозначения:

X – измеряемое напряжение, Y – показание вольтметра.

Из условия задачи следует, что величина X – двоичная,

причем x1 1; x2 0; p x1 0, 9; p x2

0,1.

Сигнал Y есть непрерывная случайная величина, и для нее заданы условные плотности вероятности:

W

y x1

0,5,

0

y

 

2,

0,

y

0,

y

2,

 

 

W

y x2

1,

0,5

y

 

0,5,

0, y

0,5,

y

0,5.

 

 

Рассматриваемый канал является дискретнонепрерывным, так как входной сигнал дискретен, а выходной непрерывен. Требуется найти среднюю взаимную информацию

I(X;Y).

Найдем безусловную плотность вероятности выходного сигнала:

W y p x1 W y x1

 

p x2 W y x2

0,

y

0, 5,

0,1,

0, 5

y

0,

0, 55,

0 y

0, 5,

0, 45,

0, 5

y

2,

0,

2

y.

 

Далее вычисляем величину средней взаимной информации, учитывая соотношение (3.1.3)

I X ;Y p x1 I Y ; x1

p x2 I Y ; x2

 

2

 

W

y x1

 

p x

W y x

log

dy

 

 

1

1

 

W

y

 

0

 

 

 

 

 

 

154

 

0.5

 

W

y x2

 

p x

 

W y x log

dy

 

 

 

2

 

2

W

y

 

0.5

 

 

 

 

 

 

0,5

0, 5

 

0, 9 0, 5 log

dy

0, 55

0

 

 

 

2

0,5

0, 5 log 0, 5 dy 0, 45

0

0,1

0,5

1 log 0,11 dy

0,5

0

 

1

 

1 log

0, 55 dy

0, 2809 бит.

ЗА Д А Ч И

6.1.На выходе линейной части демодулятора двоичного ФМ-сигнала напряжение полезного сигнала принимает значения +2 В или –2 В. Среднеквадратическое значение нормального шума равно 0,7 В.

а) Определить битовую вероятность ошибки при его работе

вжестком режиме.

б) В мягком режиме демодулятор обеспечивает битовую вероятность ошибки 10–6. Найти вероятность стирания символа.

6.2.Вероятность ошибки на выходе демодулятора некогерентной двоичной СПИ с ортогональными сигналами составляет 0,002. Имеет ли смысл, не увеличивая мощности передатчика, применить код Рида–Малера (8,4)?

6.3.Для некогерентной СПИ с ЧМ (сигналы ортогональны,

ачастоты несущих кратны частоте следования символов) при неизменной мощности передатчика рассматриваются два варианта, при которых форма переданного сигнала одна и та же:

а) каждый информационный символ передается пять раз, декодер выносит решение по ―большинству голосов‖;

б) кодирование не применяется, то есть производится прием ―в целом‖.

Показать, который из вариантов обеспечивает меньшую величину битовой вероятности ошибки.

6.4.Флуктуации амплитуды сигнала на выходе многолуче-

вой линии при A 0 приближенно описываются нормальным

155

законом распределения вероятности с параметрами: m 6, 2. Линия связи работоспособна, если A Aп 1, 5 .

а) Определить вероятность нарушения связи; б) Сделать то же для случая, когда применяется автовыбор

максимального сигнала из трех разнесенных; а) Сделать то же для случая, когда применяется линейное

сложение сигналов после линейного детектирования.

Во всех случаях полагать, что суммарная мощность сигналов не зависит от кратности разнесения.

6.5.Найти вероятность ошибки при демодуляции ортогональных двоичных сигналов на выходе некогерентной радиорелейной линии с одним ретранслятором-регенератором, если отношение сигнал/шум на выходе одного пролета равно 20 дБ.

6.6.Определить максимальное число каналов ТЧ в МСС ВРК-АИМ, если длительность канального импульса в групповом сигнале не может быть меньше 1 мс.

6.7.Какая двоичная последовательность передана в СПИ с ОФМ, если начальные фазы принимаемых импульсов с шумом относительно текущей фазы местного опорного генератора рав-

ны … 63, 243, 242, 240, 59, 60, …?

6.8.Какая двоичная последовательность передана в СПИ с двукратной ОФМ, если начальные фазы принимаемых импульсов с шумом относительно текущей фазы местного опорного генератора равны … 38, 41, 223, 127, 309, 309, …?

6.9.Радиорелейная линия содержит 10 одинаковых участков. Вероятность ошибки при некогерентном приеме одного из двух ортогональных сигналов на одном участке равна 10–6.

Найти битовую вероятность ошибки на выходе линии при использовании ретрансляторов:

а) без регенерации сигнала; б) с регенерацией двоичного сигнала.

в) в случае, когда один из девяти ретрансляторов является регенератором, расположенным наилучшим образом.

156

7 МНОГОКАНАЛЬНАЯ ПЕРЕДАЧА И МНОГОСТАНЦИОННЫЙ ДОСТУП

Система передачи информации из одного пункта в другой называется многоканальной (n-канальной), если в ней по одному кабелю осуществляется одновременная передача n сообщений.

Многостанционным доступом (МД) называется метод, позволяющий n станциям радиосвязи (возможно, разбросанным на большой территории) совместно использовать ресурсы одного ретранслятора.

Возможные методы реализации обеих технологий одинако-

вы.

Чтобы отсутствовали междуканальнве помехи, необходимо и достаточно, чтобы система n функций, описывающих канальные сигналы, была линейно независимой при любых значениях передаваемых сообщений. При этом желательно, чтобы канальные сигналы были к тому же попарно ортогональны.

Канальные сигналы не перекрываются во времени – это ме-

тод временного разделения каналов (ВРК).

Спектры канальных сигналов не перекрываются на оси час-

тот – это метод частотного разделения каналов (ЧРК).

Все канальные сигналы передаются одновременно в одной общей полосе частот (их спектры также перекрываются), но взаимная ортогональность сигналов обеспечена тем, что все они имеют разную форму. Это метод кодового разделения каналов

(КРК).

РЕШЕНИЕ ТИПОВЫХ ПРИМЕРОВ

Пример 6.1.

.

Решение. Введем обозначения: X – напряжение в сети,

V – ошибка измерения,

Y = X + V – показание прибора.

Из условия задачи записываем плотности вероятностей:

W x

 

 

1

 

exp

x

mx

2

,

 

 

 

 

2

x2

 

 

 

2

 

x

 

 

157

W y x

 

1

 

exp

y

x

2

.

 

 

 

 

 

 

 

 

 

2

v2

 

2

 

 

v

 

 

Безусловную плотность вероятности величины Y можно найти по общей формуле (1.3), но проще поступить следующим образом. Показание прибора Y есть сумма двух независимых нормальных случайных величин и, следовательно, Y также имеет нормальное распределение с математическим ожиданием

 

 

 

 

 

 

 

 

my

mx

mv

mx

 

 

220 В

 

 

 

 

 

 

и дисперсией

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

 

 

2

 

104 В2 .

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

x

 

 

 

v

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Итак,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W y

1

 

 

 

exp

 

 

 

y

mx

2

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2 y2

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Условную плотность вероятности х находим по формуле

(1.4)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W x y

W

y x W

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

W

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

y x 2

 

 

 

 

 

2

 

 

 

2

 

 

 

 

 

2

 

y

 

exp

 

1

 

 

 

 

 

 

x mx

 

y mx

.

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

2

 

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

v

x

 

 

 

 

 

 

v

 

 

 

 

x

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

В выражении, стоящем под знаком экспоненты, осуществляем возведение в квадрат и затем группируем члены, содержащие х2 и х. В итоге убеждаемся, что условное распределение величины х также нормально

 

1

 

 

x S

 

y

2

 

W x y

 

exp

 

 

,

 

 

 

 

 

 

 

 

 

 

2

2

 

 

2

 

 

 

 

 

 

 

2

где S y m x x y m x – условное математическое

2 y

ожидание X,

 

 

 

 

158

 

2

 

2

 

2

x

 

v

- условная дисперсия X.

 

 

2

 

 

 

 

 

y

Для ответа на вопрос п. а) следует по формуле (3.1.2) вычислить величину средней взаимной информации между ансамблем X и реализацией у

I X ; y M ln W X y W X

 

 

 

X S

y

2

 

X

m

 

2

 

M ln

x

 

 

 

x

.

 

 

 

 

 

 

 

 

 

2

2

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

Находим квадраты разностей и выносим за знак математического ожидания слагаемые и множители, не зависящие от х. Далее учитываем, что вычисляются условные математические ожидания при конкретном значении у, поэтому

M X S y , M X 2

 

S 2 y

2 .

В итоге получаем

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

2

 

 

 

 

2

 

 

 

 

1

 

 

 

1

 

 

 

 

 

y

mx

 

 

I X ; y

ln

 

y

 

 

x

 

 

1

2

2

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

v

 

 

y

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

ln

104

 

 

100

 

 

 

 

y

220 2

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2 104

 

 

 

104

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

1,629

0, 4801

 

 

 

y

220 2

1

нат.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

104

 

 

 

 

Таким образом, искомая зависимость есть параболическая функция разности y m x , причем наименьшее количество информации, равное 1,1482 нат, доставляет наиболее вероятное показание прибора y m x 220 В .

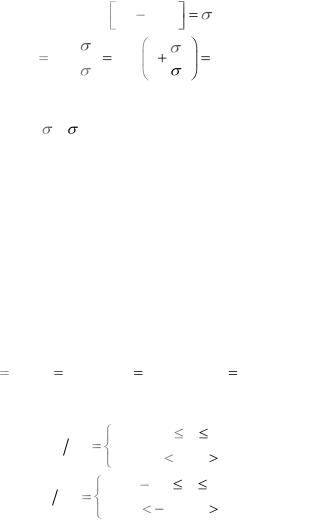
Для ответа на вопрос п. б) необходимо найти среднюю величину взаимной информации между ансамблями X и Y. Вычисляем безусловное математическое ожидание величины I(Х; у).

159

При этом учитываем, что M Y

m

2

 

2

, и получаем

 

 

 

 

 

 

 

x

 

y

 

 

1

 

2

 

1

 

 

 

2

 

 

I X ;Y

ln

y

ln

1

 

x

1,629 нат.

2

2

2

 

2

 

 

 

 

 

 

 

 

 

v

 

 

 

v

 

 

 

 

 

 

 

 

 

 

 

 

Обратите внимание, что в среднем количество получаемой информации в данном примере зависит только от отношения

«сигнал/ошибка» x v .

Пример 6.2. Для контроля исправности блока периодически измеряют значение напряжения в контрольной точке схемы. Если блок исправен, то это напряжение равно 1 В, в противном случае – 0 В. Ошибка вольтметра распределена равномерно с нулевым математическим ожиданием, но ширина этого распределения зависит от величины измеряемого напряжения: она равна 2 В, если напряжение на входе 1 В, и 1 В – в противном случае. В среднем в 90% времени блок исправен.

Найти количество информации, доставляемой прибором при одном измерении.

Решение. Введем обозначения:

X – измеряемое напряжение, Y – показание вольтметра.

Из условия задачи следует, что величина X – двоичная,

причем x1 1; x2 0; p x1 0, 9; p x2

0,1.

Сигнал Y есть непрерывная случайная величина, и для нее заданы условные плотности вероятности:

W

y x1

0,5,

0

y

 

2,

0,

y

0,

y

2,

 

 

W

y x2

1,

0,5

y

 

0,5,

0, y

0,5,

y

0,5.

 

 

Рассматриваемый канал является дискретнонепрерывным, так как входной сигнал дискретен, а выходной непрерывен. Требуется найти среднюю взаимную информацию

I(X;Y).

Найдем безусловную плотность вероятности выходного сигнала:

160

W y p x1 W y x1

 

p x2 W y x2

0,

y

0, 5,

0,1,

0, 5

y

0,

0, 55,

0 y

0, 5,

0, 45,

0, 5

y

2,

0,

2

y.

 

Далее вычисляем величину средней взаимной информации, учитывая соотношение (3.1.3)

I X ;Y p x1 I Y ; x1

p x2 I Y ; x2

 

2

 

W

y x1

 

 

p x

W y x

log

dy

 

 

 

1

1

 

W

y

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

0.5

 

 

W

y x2

 

p x

W y x log

dy

 

 

2

 

2

 

 

W

y

 

0.5

 

 

 

 

 

 

 

 

 

 

 

0,5

0, 5

 

0, 9 0, 5 log

dy

0, 55

0

 

 

 

2

0,5

0, 5 log 0, 5 dy 0, 45

0

0,1

0,5

1 log 0,11 dy

0,5

0

 

1

 

1 log

0, 55 dy

0, 2809 бит.

ЗА Д А Ч И

7.1.В СПИ с многостанционным доступом с кодовым разделением каналов база сигнала равна 128, а закон двоичной внутриимпульсной ФМ для каждого абонента задан случайным образом. Найти математическое ожидание и СКО отношения сигнал/помеха в зависимости от числа активных мешающих станций, полагая, что мощности всех сигналов (полезного и мешающих) на входе приемника одинаковы.

7.2.Система МДКР рассчитана на одновременную передачу 32 стандартных цифровых телефонных сигналов. Найти ширину главного лепестка в спектре сигнала на выходе такой СПИ.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности