
2059
.pdf
11
Eвх |
|
|
|
|
ω1, k1 |
|
|
|
? |
|
Pnl[(ω1+ ω2), (k1+ k2)] |
|
||
|
|
|
||
|
|
Pnl[(ω1- ω2), (k1- k2)] |
|
|
ω2, k2 |
|
E[ω3, k3] |
|
|
|
|
|
|
|
|
|
|
|
|
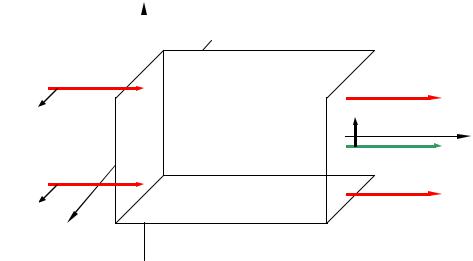
Рис. 1. Нелинейная поляризация среды на суммарной и разностной частотах и результирующее поле распространяющейся в ней световой волны с частотой ω3 и волновым вектором k3
Очевидно, что если одновременно выполняются условия
3 1 |
2 , |
(24) |
k3 k1 |
k2 , |
(25) |
то будет генерироваться волна с суммарной частотой. В случае выполнения условий
3 1 |
2 , |
(26) |
k3 k1 |
k2 , |
(27) |
в среде происходит эффективная генерация на разностной частоте. Отметим, что условия синхронизма такого же вида, как и (24)-(25) или (26)-(27), широко используются при описании многих явлений взаимодействия световых волн. Например, подобные условия синхронизма являются ключевыми при анализе дифракции света на акустических волнах и на объемных голограммах.
Эти условия выражают законы сохранения энергии ((24) и (26)) и квазиимпульса ((25) и (27)). То есть, взаимодействие двух фотонов с энергиями ħω1 и ħω2 и квазиимпульсом ħk1 и ħk2 порождает фотон с энергией ħω3 = ħω1 + ħω2 (или с энергией ħω3 = ħω1 – ħω2) и квазиимпульсом ħk3 = ħk1 + ħk2 (или ħk3 = ħk1 – ħk2). Закон
12
сохранения энергии всегда выполняется точно, а условие синхронизма для квазиимпульса может выполняться с некоторой расстройкой:
k k3 (k1 k2 ) 0 . |
(28) |
В общем случае условия синхронизма, налагаемые на волновые векторы взаимодействующих волн, являются векторными. Однако в большинстве случаев наиболее эффективным является коллинеарное взаимодействие, которое и будет рассмотрено ниже.
4. Генерация волны суммарной частоты при коллинеарном взаимодействии в ниобате лития
Как следует из (15), в кристалле ниобата лития отличны от нуля 8 коэффициентов тензора d, то есть существует достаточно много вариантов нелинейного взаимодействия. По причинам, которые станут ясны в дальнейшем, рассмотрим взаимодействие, основанное на использовании нелинейной восприимчивости d31 = d311. В этом случае световые волны с частотами ω1 и ω2 должны быть поляризованы по оси x, а волна суммарной частоты – по оси z. Таким образом, взаимодействие должно быть между двумя обыкновенно поляризованными волнами (oo) и необыкновенной волной (e), распространяющейся вдоль оси y (рис. 2).
|
|
|
|
z |
|
|||||
|
|
ω1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
e1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
e3 |
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2 |
|
|
|
|
|
ω3 |
= ω1+ ω2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
e2
x
Рис. 2. Коллинеарное взаимодействие волн типа oo – e в кристалле ниобата лития
13
Запишем поля для всех трех волн:
E |
(1) |
( y,t) |
1 |
m1 |
( y)exp[i( t k y)] к.с., |
(29) |
|||||||
|
2 |
E |
|
||||||||||
1 |
|
1 |
|
1 |
1 |
|
|
|
|
|
|||
E |
(2) |
( y,t) |
1 |
m2 |
( y)exp[i( t k |
|
y)] к.с., |
(30) |
|||||
|
|
E |
|
|
|||||||||
1 |
|
2 |
1 |
|
2 |
|
2 |
|
|
|
|
||
E |
(3) |
( y,t) |
1 |
m3 |
( y)exp{i[( )t k |
|
y)] к.с., |
(31) |
|||||
|
2 |
E |
|
|
|||||||||
3 |
|
|
3 |
|
1 |
|
2 |
3 |
|
|
|||
где мы учли условие синхронизма ω3 = ω1+ ω2. Найдем нелинейную поляризацию на частоте ω3:
P |
nl |
(t, y) |
d |
|
m |
m |
( y)exp{i[( )t (k |
+ k |
|
) y]} к.с. |
(32) |
||
|
31 |
E |
( y)E |
2 |
|||||||||
3 |
0 |
|
1 |
1 |
1 |
2 |
1 |
|
|
|
|||
Будем использовать далее волновое уравнение (23), упростив его следующим образом:
2E |
2 |
(ε E) |
|
|
2P |
(33) |
0 |
t2 |
0 |
nl . |
|||
|
|
t2 |
|
Здесь мы отбросили малый член grad(divE), который не равен нулю только при распространении под углом к оптической оси, отличным от 00 и 900.
|
|
|
Подставляя |
E(3) |
и |
Pnl в (33), получаем |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
d |
2 m3 |
|
|
|
|
|
m3 |
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
m3 |
|
|
|
|
|
|
|||||
|
|
E |
|
|
|
|
dE |
|
k |
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
3 |
2ik |
3 |
|
|
|
3 |
|
3 |
|
|
0 |
n 1 |
|
|
( |
) |
|
|
|
exp[i( )t k |
y] |
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2 |
|
dy |
|
|
|
|
dy |
|
|
|
|
|
0 |
|
e |
|
|
1 |
|
|
|
3 |
1 |
|
3 |
|
(34) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
( ) |
2 |
|
d |
|
m1 m2 |
exp{i[( )t |
(k |
k |
) y]}. |
|
|
|
|
|
|
|||||||||||||||||||||
0 |
|
|
|
E |
E |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
0 |
|
31 1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
||||||
Точно такое же уравнение можно записать и для комплексно-сопряженных членов, которые будут в резонансе друг с другом. Воспользуемся далее известным соотношением для k3 и ω3:
k |
3 |
|
|
|
0 |
n 3 |
|
|
3 n 3 . |
(35) |
|
|
|
0 |
|
e |
3 |
|
c |
e |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
14
В этом случае член |
k |
2 |
|
|
|
|
|
|
2 |
( ) |
2 |
E |
m3 |
в уравнении (34) обращается в |
|||||||
3 |
0 |
|
n 1 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
0 |
|
e |
|
1 |
|
|
3 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ноль. Воспользуемся также приближением медленно меняющихся амплитуд |
|||||||||||||||||||||
|
d |
2 m3 |
|
|
|
|
m3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
2k |
|
dE |
|
, |
|
|
|
|
|
|
|
|
|
|
|
(36) |
|||
|
|
3 |
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
dy2 |
|
dy |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и приведем уравнение (34) к виду
m3 |
|
|
|
( 3 ) |
2 |
|
m1 |
m2 |
|
dE3 |
|
|
|
|
|
|
|||
|
i |
|
0 |
|
d |
311 |
E |
E |
exp(i ky) , |
|
|
||||||||
dy |
0 |
|
k3 |
|
1 |
1 |
|
||
|
|
|
|
|
|
|
|
или
m3 |
|
3 |
|
m1 |
m2 |
|
|
dE3 |
|
|
|
||||
|
i |
|
d |
E |
E |
exp(i ky) . |
|
dy |
cn 3 |
||||||
|
|
311 1 |
1 |
|
|||
|
|
e |
|
|
|
|
По аналогии запишем уравнения для E1m1 и E1m2 :
m1 |
|
|
1 |
|
|
|
|
|
|
|
|||
dE1 |
|
i |
|
d131E3m3 E1m2 |
|
exp( i ky) , |
|||||||
dy |
|
|
|
||||||||||
|
|
cn |
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
d E1m2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
i |
|
|
|
2 |
|
d131 E3m3 |
|
E1m1 exp(i ky) . |
||
dy |
|
cn |
|
2 |
|||||||||
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
(37)
(38)
(39)
(40)
Уравнения (38)-(40) описывают связь амплитуд волн с частотами ω1, ω2 и ω3 = ω1+ ω2 и их взаимное влияние друг на друга. При отсутствии нелинейности, d311 = d131 = 0, имеем dE1m1 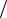 dy dE1m2
dy dE1m2 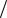 dy 0 , а также dE3m3
dy 0 , а также dE3m3 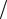 dy 0 , то есть амплитуды входных волн
dy 0 , то есть амплитуды входных волн
E1m1 и E1m2 не изменяются в кристалле, а волны на суммарной частоте не возникает
( E3m3 0 ).

15
5. Генерация второй гармоники
Первый эксперимент по генерации второй гармоники выполнили в 1961 году Франкен, Хилл, Петерс и Вейнрейх (рис. 3).
Рис. 3. Рисунок из книги Ярив А., Юх П. Оптические волны в кристаллах: Пер. с
англ. – М.: Мир, 1987.
В эксперименте было обнаружено, что наряду с основным излучением на выходе кристалла существует вторая гармоника с длиной волны λ = 347,15 нм (ультрафиолетовое излучение). Эффективность преобразования по мощности составила в данном эксперименте 10-8. В настоящее время при генерации второй гармоники достигаются значения эффективности, близкие к единице.
Проведем далее анализ эффективности генерации второй гармоники на основе уравнений (38)-(40). В случае генерации второй гармоники ω1 = ω2 и ω3 = 2ω1. Поэтому нам понадобятся лишь два уравнения:
m3 |
|
1 |
|
|
|
m1 |
|
2 |
|
|
|
|
|
dE3 |
|
|
|
|
|
|
|
|
|
||||
|
|
i |
|
|
d |
|
(E |
) |
|
exp(i ky) , |
(41) |
||
dy |
|
|
|
|
|||||||||
|
cn2 1 |
311 |
1 |
|
|
|
|
|
|
||||
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
m1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
dE1 |
|
i |
d131E3m3 E1m1 |
|
exp( i ky) . |
(42) |
|||||||
dy |
|
|
|||||||||||
|
cn 1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
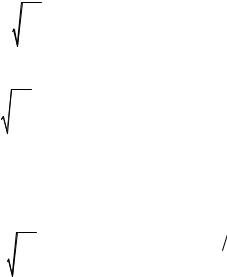
16
где учтено, что в случае генерации второй гармоники нелинейная поляризация определяется соотношением (10), а не (7).
Рассмотрим далее приближение неистощимой накачки, при котором лишь малая
часть основной волны преобразуется во вторую гармонику. |
В этом случае можно |
||||||||||||
|
m1 |
) |
2 |
не зависит от координаты y, и уравнение (41) сразу интегрируется. |
|||||||||
считать, что (E |
|
|
|||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Для граничного условия |
m3 |
(0) 0 на входной грани кристалла (при y = 0) получаем |
|||||||||||
E |
|||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
m3 |
|
|
|
1 |
|
|
m1 |
|
2 |
exp(i ky) 1 |
|
|
|
E |
( y) i |
|
|
|
|
d |
|
(E |
) |
|
|
. |
(43) |
cn2 1 |
|
|
i k |
||||||||||
3 |
|
|
31 |
1 |
|
|
|
|
|||||
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
Выразим интенсивность второй гармоники, используя соотношения
I |
(2 |
) |
|
|
1 |
n |
2 |
|
|
0 |
|
m3 |
|
|
2 |
|
||||||
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
e |
|
|
0 |
|
3 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
( ) |
|
1 |
|
|
|
|
0 |
|
|
m1 |
|
2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
I |
|
|
|
|
|
n |
|
|
|
|
|
|
E |
|
|
. |
|
|||||
|
|
|
|
2 |
|
o |
|
|
0 |
|
|
1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В результате получаем
I (2 ) (L) 2 |
0 |
2d312 L2 |
(I ( ) )2 |
sin2 kL 2 |
. |
(44) |
c2 no 2 ne2 |
|
|||||
|
0 |
|
kL / 2 2 |
|
||
Таким образом, интенсивность второй гармоники пропорциональна квадрату интенсивности основного излучения. Поэтому использование фокусирующей линзы, такой, которая использовалась в эксперименте, иллюстрируемом рис. 3, приводит к увеличению эффективности преобразования основного излучения во вторую гармонику.
6. Фазовый синхронизм при генерации второй гармоники
Очевидно, что эффективность генерации второй гармоники (ГВГ) максимальна при точном выполнении условия фазового синхронизма ( k = 0):

|
17 |
k3 k2 k1 0 , |
(45) |
причем для ГВГ имеем, при рассмотренном выше процессе oo – e:
2 1 n |
(2 ) |
1 n |
( ) |
1 n |
( ) 0 , |
|||
c |
e |
1 |
c |
o |
1 |
c |
o |
1 |
|
|
|
|
|
|
|||
или
ne (2 1 ) no ( 1 ) . |
(46) |
Это условие, как правило, не выполняется. Например, в кристалле KH2PO4 (дигидрофосфат калия, сокращенно – KDP), часто используемом для различных нелинейных устройств, при комнатной температуре для λ3 = 0.5 мкм no = 1.5149 и ne = 1.4725, а для λ1 = 1.0 мкм no = 1.4960 и ne = 1.4610. Чтобы определить, как это скажется на эффективности ГВГ, рассмотрим присутствующий в (44) множитель
sin2 kL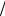 2 ,
2 ,
kL / 2 2
экстремумы которого обеспечивают экстремумы в выходной интенсивности 2-й гармоники. Условие экстремума определяется, как
k |
Lp |
|
(2 p 1), |
p 0,1,2,..., |
(47) |
2 |
|
2 |
|
|
|
а расстояние между соседними максимумами в выходной интенсивности равно
2L |
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
. |
(48) |
k |
2 |
|
n |
( |
|
) 2 2 |
n |
( ) |
2 |
|
n2 n |
|
|||||||
c |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
e |
|
|
o |
|
|
|
e |
o |
|
|
||||
Расстояние Lc называется длиной когерентности, поскольку в ее пределах нелинейная поляризация находится в фазе с полем плоской волны, соответствующей второй гармонике. При λ1 = 1.0 мкм и ne2 no 0.025 получаем, что Lc = 10 мкм.
18
Обычно толщина нелинейного кристалла составляет 10 мм и более. Если удастся увеличить Lc до этих значений, то выигрыш в интенсивности 2-й гармоники составит 106 раз. Как это можно сделать?
Условию ne (2 1 ) no ( 1 ) можно удовлетворить, если взаимодействие волн осуществлять не при их распространении перпендикулярно оптической оси, а под некоторым углом θ. В этом случае необыкновенная волна характеризуется показателем преломления
(n |
2 |
|
|
|
n2 n2 |
|
|
|
|
o e |
|
|
|
||||
|
) |
|
|
|
|
, |
||
|
(n2 )2 |
cos2 |
(n2 )2 sin2 |
|
||||
|
|
|
|
e |
|
o |
|
|
аобыкновенная – no(ω). Если первая поверхность представляет эллипсоид вращения, а
еесечение любой плоскостью, проходящей через оптическую ось – эллипс, то вторая поверхность является сферой (ее сечение такой же плоскостью – окружность). Для одноосных кристаллов, таких как KDP и ниобат лития, имеются точки пересечения
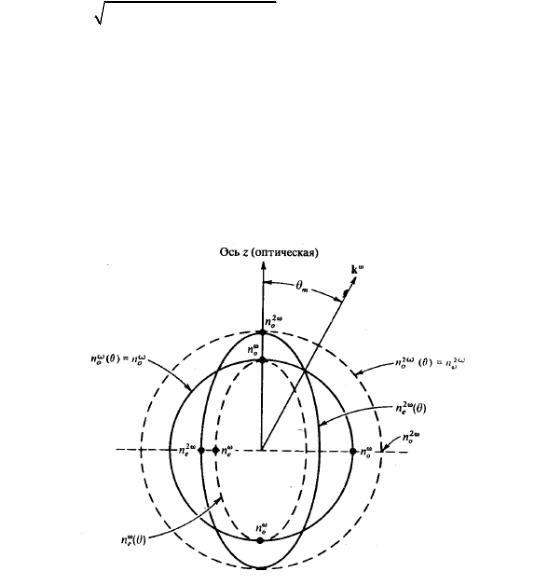
окружности no(ω1= ω) с эллипсом n’(ω3=2ω) (рис. 4), где k = 0, а Lc .
Рис. 4. Поверхности показателей преломления для обыкновенной и необыкновенной волн в отрицательном одноосном кристалле (no>ne).
19
Отметим, что показатели преломления кристаллов зависят от температуры. Поэтому другой способ достижения фазового синхронизма заключается в нагреве кристалла до температуры, при которой ne (2 1 ) no ( 1 ) . Для ниобата лития, выращенного из расплава с соотношением Li/Nb, близким к стехиометрическому, при генерации второй гармоники излучением неодимового лазера (λ1 = 1064 нм), эта температура может составлять около 150 0С. Достоинство этого подхода в том, что при такой температуре исчезает фоторефрактивный эффект (optical damage), и структура выходного пучка не искажается с течением времени.
7. Генерация второй гармоники при наличии обратного воздействия
Рассмотрим самосогласованную задачу о генерации второй оптической гармоники, то есть учтем эффект истощения (уменьшения мощности) волны накачки. Воспользуемся уравнением (41) и уравнением, комплексно сопряженным к (42), полагая в них для простоты k = 0 и учитывая, что в случае мгновенного отклика d311 = d131 = d31. В результате получаем
m3 |
|
|
|
|
|
1 |
|
|
|
|
m1 |
|
2 |
|
|
|
|
||
dE3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
i |
|
|
|
|
d |
|
|
(E |
) |
|
, |
|
|
(49) |
||||
dy |
cn2 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
31 |
|
1 |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
m1 |
) |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
d (E1 |
|
|
i |
d |
|
|
m3 |
|
|
m1 |
|
|
|||||||
dy |
|
|
|
cn 1 |
31 |
(E |
|
) |
|
E |
. |
(50) |
|||||||
|
|
|
|
|
|
|
3 |
|
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
|
|
|
|
|
Рассматриваемая система уравнений для двух комплексных функций (то есть в целом
для |
четырех |
функций, |
|
определяющих действительные и мнимые части |
|
|
m1 |
( y) и |
||||||||||||||||
|
|
E |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
m3 |
( y) ) является нелинейной. Как найти ее решение? |
|
|
|
|
|
|
|
||||||||||||||||
E |
|
|
|
|
|
|
|
|||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обратим внимание, что если первое уравнение умножить на |
n2 1 |
|
0 |
|
0 |
(Em3 ) , а |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
3 |
|||
второе на n 1 |
|
0 |
|
Em1 |
и сложить полученные результата, то члены в правой части |
|||||||||||||||||||
|
|
|
o |
|
|
|
0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
итогового уравнения взаимно уничтожаются: |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
0 |
|
|
|
|
|
m3 |
|
|
0 |
|
m1 |
) |
|
|
|
|
|
|
|
|
||
|
|
|
m3 |
|
|
dE3 |
|
|
|
m1 |
d (E1 |
|
|
|
|
|
|
|
|
|
||||
|
n |
0 |
(E |
) |
|
|
dy |
n |
|
E |
dy |
|
|
0 . |
|
|
|
|
|
|
(51) |
|||
|
e |
|
3 |
|
|
|
|
o 0 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||

20
Складывая (51) с комплексно-сопряженным к нему уравнением, получаем первый интеграл нелинейной системы уравнений (49)-(50) в следующем виде:
d |
|
1 |
|
0 |
|
m3 |
|
2 |
|
1 |
|
0 |
|
|
m1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
ne |
|
|
E3 |
|
|
|
|
no |
|
|
|
E1 |
|
|
|
0 , |
(52) |
|
|
2 |
|
0 |
|
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
или, с учетом соотношений для интенсивностей волны накачки и ее второй гармоники (см. раздел 5), в другом виде:
d |
|
2 |
( y) I |
|
|
0 . |
(53) |
|
|
|
|||||
dy |
I |
|
|
( y) |
|||
|
|
|
|
|
|
|
Решение данного уравнения, с учетом граничного условия I 2 (0) 0 , имеет вид
I 2 ( y) I ( y) I (0) , |
(54) |
и выражает закон сохранения энергии – два кванта с энергией ħω1 рождают квант с энергией ħω3 = 2ħω1. Соответственно, число рожденных квантов второй гармоники в два раза меньше числа исчезнувших квантов основной частоты.
Выразим из (54) квадраты модулей амплитуд:
m1 |
|
2 |
|
m1 |
|
2 |
|
ne2 1 |
|
|
m3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
E |
( y) |
|
|
E |
(0) |
|
|
|
|
|
E |
( y) |
|
. |
(55) |
|
|
|
|
||||||||||||
1 |
|
|
|
1 |
|
|
|
n 1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|
|
|
|
|
|
Если входную амплитуду основной волны выбрать вещественной, E1m1 (0) E1m1(0) , то ее амплитуда в кристалле также будет вещественной, E1m1 ( y) E1m1 ( y) , а амплитуда второй гармоники E3m3 ( y) (см. уравнение (49)) – чисто мнимой величиной. Делая
замену |
m3 |
( y) iE |
m3i |
( y) и |
используя |
интеграл |
сохранения в виде (55), из (49) |
|||||||||||
E |
|
|
||||||||||||||||
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
dE3m3i |
|
|
1 |
|
|
m1 |
|
2 |
|
1 |
|
|
m3i 2 |
|
|
||
|
|
|
|
|
d31 E1 |
(0) |
|
|
|
d31 |
E3 |
|
. |
(56) |
||||
|
|
dy |
cn 1 |
cn 1 |
||||||||||||||
|
|
|
|
|
e |
|
|
|
|
|
|
o |
|
|
|
|
|
|
