
ЛР 1
.docxМинистерство образования Республики Беларусь
Учреждение образования
«Белорусский государственный университет информатики и радиоэлектроники»
Институт информационных технологий
Факультет компьютерных технологий
Лабораторная работа № 1
«Задача о планировании оптимальной производственной программы»
Вариант № 23
Выполнил: студент гр. 981064 Харевич В.О.
Проверила: Бородина Т.А.
Минск 2020
Лабораторная работа № 1
«Задача о планировании оптимальной производственной программы»
Вариант № 23
Задание
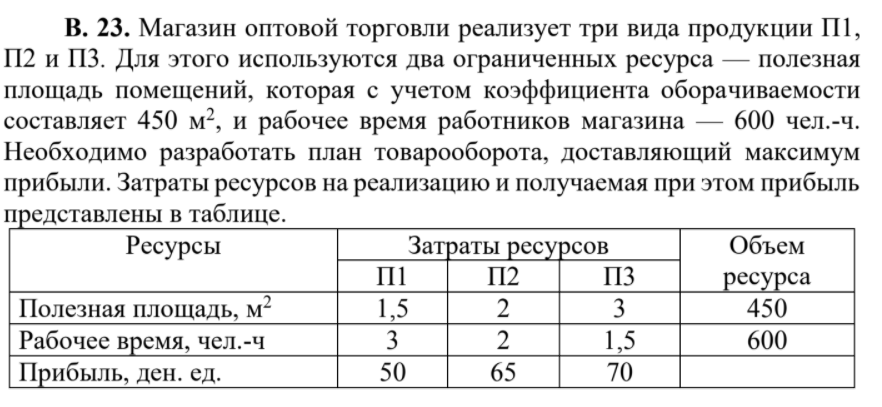
x1, x2, x3 – количество продукции 1-го, 2-го, 3-го вида, которую необходимо произвести для получения максимальной прибыли. Математическая модель задачи:
f = 50x1 + 65x2 + 70x3 (max)

y1, y2 – полезная площадь и рабочее время соответственно, которое необходимо затратить для производства одной единицы продукции. Математическая модель двойственной задачи:
φ = 450y1 + 600y2 (min)
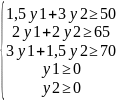
Оптимальный план
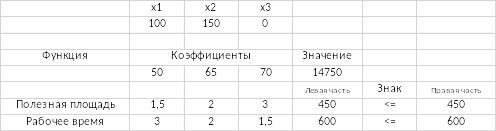
Анализ оптимального решения
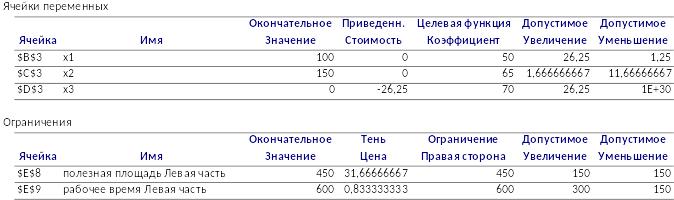
Отчет о результатах:
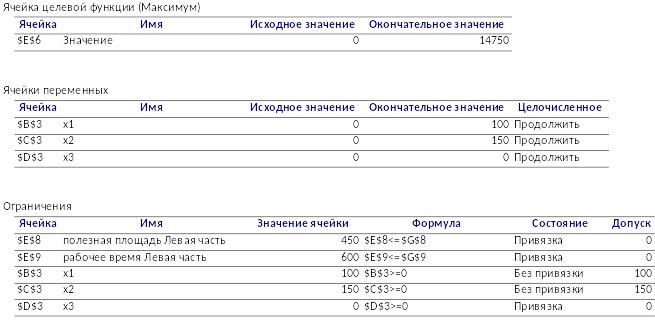
Отчет об устойчивости:
Отчет о пределах:
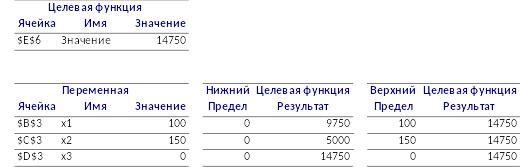
а) В оптимальный план вошла продукция П1 и П2. Для получения максимальной выгоды необходимо производить 100 единиц П1 и 150 единиц П2. Производство продукции П3 является невыгодным.
б) Дефицитными ресурсами являются полезная площадь и рабочее время, т.к. истрачены все запасы данных ресурсов
в) Оптимальное решение двойственной задачи: u = 31,67 * 450 + 0.83 * 600 = 14750
г) Исходя из оптимального решения двойственной задачи дефицитными продуктами являются П1 и П2, а П3 является избыточным.
д) Интервал устойчивости:
Полезная площадь: [450-150; 450+150] = [300;600]
Рабочее время: [600-150; 600+300] = [450;900]
5. Двойственная задача
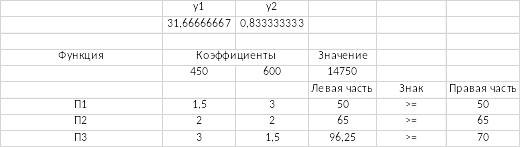
6. При увеличении каждого из ресурсов на 1 мы получаем следующее решение:
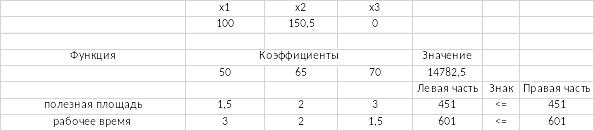
Все ресурсы также полностью израсходованы. Получили прирост П2 на 0,5, соответственно значение целевой функции увеличилось на 32,5.
