Защита от альфа-частиц

Из формул (51.6) и (51.7) следует, что проникающая способность альфа-частиц от обычных лаборатор- ных изотопных источников невелика: не более 6см в воздухе, и меньше миллиметра в твердом веще- стве. Поэтому для защиты от внешних потоков альфа-частиц в лабораторных условиях достаточ- но тонких защитных экранов, например, листа бу- маги или фольги. Для защиты рук достаточно хи- рургических перчаток.

Наибольшую опасность представляют мелкие части- чки радиоактивной пыли, которые вместе с возду- хом могут попасть внутрь организма, поэтому осо- бые меры предосторожности требуются при рабо- те с открытыми незащищенными источниками.

Защита от протонов

Внастоящее время не является редкостью примене- ние ускорителей протонов для прикладных целей, например, в медицине. При этом необходимо вы- полнение условий радиационной безопасности.

Пробег протонов с энергией Tp до 200 МэВ в воздухе

где Тp - кинетическая энергия протонов (в МэВ), A - массовое число тормозящего вещества.

Например, пробег протона с энергией 40 МэВ в воздухе по формуле (51.8) составит при-

мерно 14м. Очевидно, что для безопасной работы необходим экран, например, из ста- ли.

Массовая толщина пробега протонов с такой

энергией в стали по формуле (51.9) равна

примерно 2.55г/см2. Плотность стали равна 7.8г/см3, поэтому пробег протонов составит

примерно 3.3мм, а толщина экрана (с запа- сом) должна быть не менее 5 мм.

Прохождение легких заряженных частиц (электронов) через вещество

Прохождение электронов качественно отличается от

прохождения тяжелых заряженных частиц. Главной

причиной этого является малая масса электрона. Из- за этого изменение импульса налетающего электро-

на при каждом столкновении может быть большим.

Это приводит к тому, что электроны сильно отклоня- ются от первоначального направления движения, и, вследствие многократного рассеяния, двигаются в веществе не по прямой, а по сложной криволиней-

ной траектории. Кроме того, при резком изменении

импульса электроны испытывают большие ускоре- ния, и для них становятся существенными потери на

излучение электромагнитных волн.

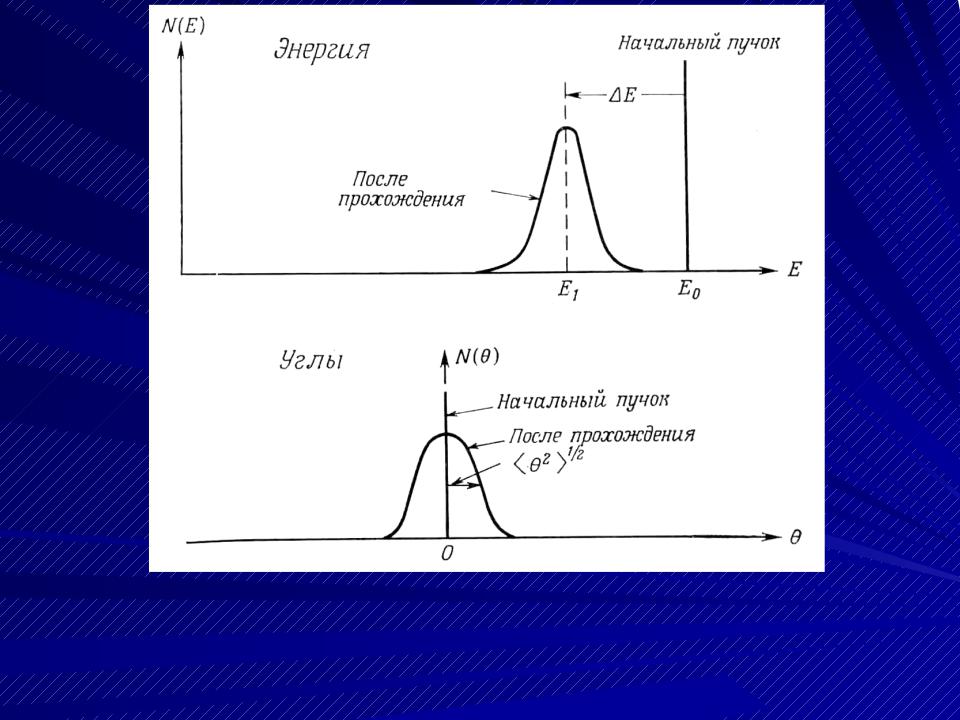
Распределения по энергиям и по углам в пучке

заряженных частиц до и после прохождения ими поглощающего слоя

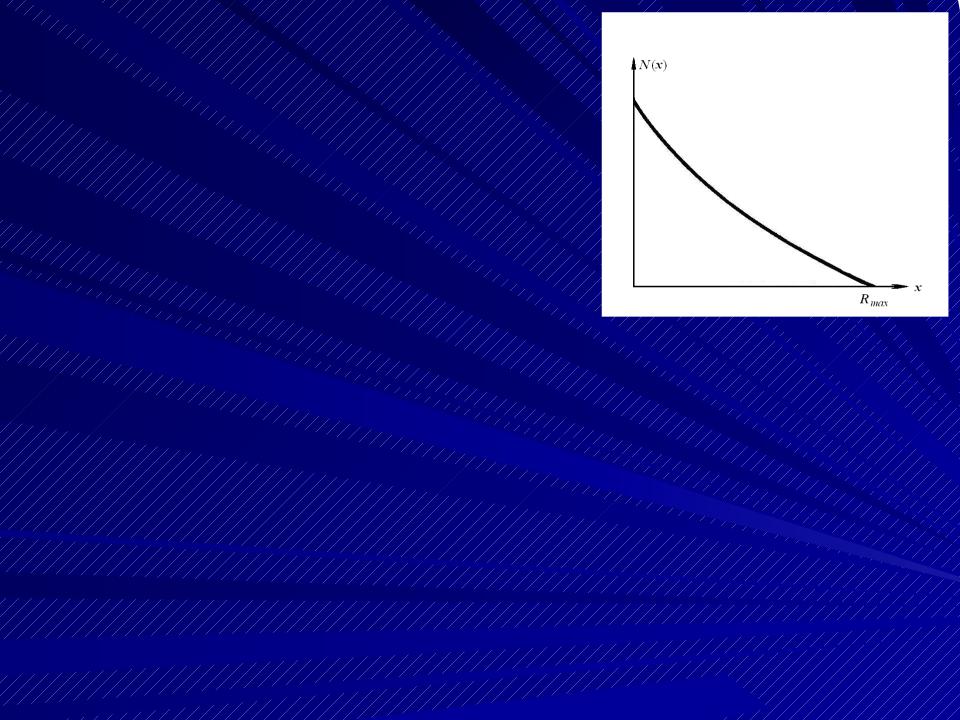
Т.к. траектория электрона не яв-

ляется прямолинейной, то вид

зависимости числа N(x) электро- нов существенно отличается от

аналогичной зависимости для тя-

желых заряженных частиц. Для электронов кривая N(x) плавно

уменьшается с увеличением толщины. Поэтому вме-

сто среднего пробега, который характеризует про- хождение тяжелых частиц, здесь используется мак- симальный пробег Rmax, т.е. минимальная толщина слоя вещества, в котором задерживаются все элек- троны. Очевидно, что максимальный пробег совпа- дает с полным, обычно криволинейным путем, кото- рый электрон проходит в веществе.

Потери энергии на излучение пропорциональны ква-

драту ускорения. Т.к. силы, действующие по закону

Кулона на протон и электрон при столкновении с атомным электроном одинаковы (т.к. одинаковы ве-

личины зарядов), то ускорения этих частиц обратно

пропорциональны их массам. Поэтому радиацион- ные потери для электронов на 6 порядков больше,

чем для тяжелых частиц. Расчет дает следующую

формулу для удельных потерь энергии электронов

где n=ρNA/A - концентрация (или плотность) атомов в

веществе, Z - зарядовое число этих атомов, NA - чис- ло Авогадро.

Сравнивая эту формулу с формулой (51.2), можно

где Te измеряется в МэВах. Из этой формулы следу-

ет, что границей двух энергетических областей (меж- ду высокой и низкой энергией) для электронов явля- ется критическая энергия, равная

Eкр ≈ (800/Z) МэВ, (51.12)

где Z - зарядовое число, т.е. число протонов в ядрах

тормозящих атомов. Например, для алюминия Eкр ≈

60МэВ, для свинца Eкр ≈ 10МэВ, и т.д. При Te < Eкр преобладают ионизационные потери, а при Te > Eкр определяющими становятся потери на излучение.

Формула для ионизационных потерь (Te < Eкр) отлича-

ется от формулы (51.2) только поправками на реля-

тивистские и квантовые эффекты:

Для электронов с энергией Te > Eкр уравнение (51.10) легко интегрируется, в результате получаем зависи- мость энергии от пройденного пути:

Расстояние, lrad на котором средняя энергия электро-

нов уменьшается из-за радиационных потерь в e

раз, называется радиационной длиной; ее можно подсчитать по формуле (51.17). Например, для

алюминия lrad ≈ 9.8 см.