Дифференцируем (2.11) по :
|
dz d 2 z |
|
q q |
2 |
|
|
|
|
dz |
|
|
dz |
|||||||||
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2z |
|
|
||||
|
|
d |
2 |
|
|
2 |
b |
2 |
|
d |
|
||||||||||
или |
|
d |
|
d 2 z |
|
2 0mv |
|
|
|
|
|
|
d |
||||||||
|
|
|
|
|
|
|
|
|
|
|
q q |
|
|
|
|
|
|||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
(2.12) |
||||
|
|
|
|
|
|
d 2 |
|
4 0mv2b2 |
|
||||||||||||
Это линейное неоднородное дифференциальное уравнение 2-го порядка. Его общее решение мож- 
но записать как сумму: любое частное решение
плюс общее решение однородного уравнения
d 2 z |
z 0 |
(2.13) |
d 2 |
Одно из частных решений уравнения (2.12) можно
найти сразу: |
z1 |
|
q1q2 |
(2.14) |
|
4 0mv2b2 |
|||
|
|
|
Уравнение (2.13) - это уравнение гармонических ко-
лебаний; вид его общего решения общеизвестен:
z0 |
Acos B sin |
|
|
||||
Таким образом, общее решение уравнения (2.12): |
|||||||
z z0 z1 Acos B sin |
|
q1q2 |
(2.15) |
||||
4 0mv2b2 |
|||||||
|
|
|
|
|
|||
Чтобы найти константы А |
и В, используем граничные |
||||||
условия. При угле |
|
расстояние от частицы до |
|||||
ядра r , следовательно, z = 0. Подставляя в |
|||||||
(2.15), находим: |
A |
q1q2 |
|
|
(2.16) |
||
|
4 0mv2b2 |
|
|||||
Чтобы найти константу В, заметим, что ордината y
любой точки траектории связана с r и соотношени-
ем y = r sin , или |
1 |
1 |
|
z |
|
|
|
|
|
||||
|
|
|
|
|
|
(2.17) |
|
y |
r sin |
sin |
|||
С другой стороны, из (2.15) с учетом (2.16), находим:
B |
z |
|
q1q2 |
|
Acos |
z |
|
|
|
q1q2 |
1 cos |
|||
|
|
|
|
|
|
|
|
|
|
|
sin |
|||
sin |
4 0mv2b2 |
sin |
|
4 0mv2b2 |
||||||||||
Подставляя сюда (2.17), получаем: |
|
|||||||||||||
|
|
|
1 |
|
|
q1q2 |
1 cos |
|
||||||
|
|
|
B |
|
|
|
|
|
|
|
|
|||
|
|
|
y |
4 0mv2b2 |
|
sin |
|
|||||||
При угле |
ордината y b , а |
cos 1 , |
|
Отсюда |
1 |
(2.18) |
|
B b |
|||
|
|
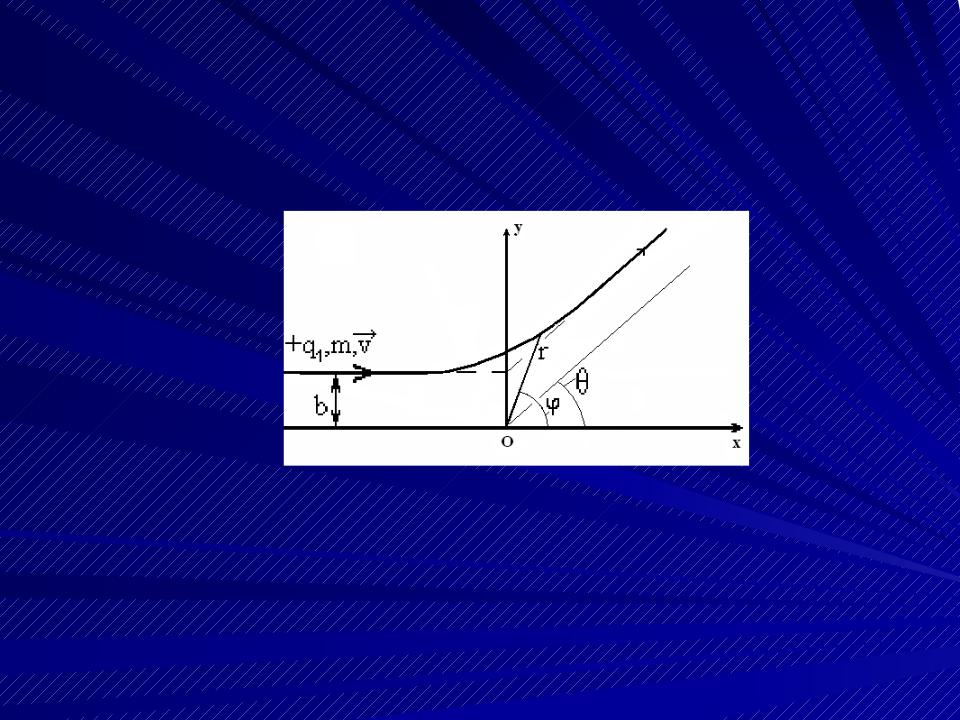
Таким образом, уравнение, связывающее r и (т.е. |
||||||||||
уравнение траектории частицы) можно записать в |
||||||||||
виде: |
z |
1 |
|
1 |
sin |
q1q2 |
|
|
1 cos |
(2.19) |
|
r |
b |
2 |
b |
2 |
|||||
|
|
|
|
4 0mv |
|
|
||||
После рассеяния угол , расстояние от части- |
|||||||
цы до ядра |
r |
, поэтому из (2.19) в пределе |
|||||
получаем |
1 |
sin |
q1q2 |
|
|
1 cos 0 |
(2.20) |
|
b |
2 |
b |
2 |
|||
|
|
4 0mv |
|
|
|||
Используя тригонометрические тождества
1 cos 2 cos2 |
|
; sin 2sin |
cos |
|
||||
|
|
2 |
|
|
|
2 |
|
2 |
запишем (2.20) в виде |
|
|
|
|
|
|
||
1 |
|
|
|
q1q2 |
|
|
2 |
|
b 2sin |
2 cos 2 |
|
|
2 cos |
|
|
||
4mv2b2 0 |
2 |
|
||||||
Отсюда получаем соотношение между углом рассея- ния θ и прицельным параметром b:
tg |
|
|
q1q2 |
|
|
|
||
2 |
4 0mv2b |
|
|
(2.21) |
||||
или |
|
|
q1q2 |
|
|
|||
|
|
|
|
|||||
b |
|
ctg |
|
|
||||
4 0mv2b |
2 |
(2.22) |
||||||
|
|
|
|
|
|
|
|
|
Для сравнения с опытом надо вычислить эффективное сечение рассеяния
Эффективное сечение равно площади кольца:
d 2 bdb |
(2.23) |
Дифференцируя уравнение (2.21), находим:
|
|
|
1 |
|
|
d |
|
q1q2db |
|
|||||
d tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 cos |
2 |
/ 2 |
4 |
2 |
b |
2 |
|||||||
|
|
|
|
|
0mv |
|
||||||||
Отсюда |
|
|
db |
|
|
4 0mv2b2d |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2q1q2 cos2 / 2 |
|
|
|
|
|||||||
Подставляя (2.22) и (2.25) в (2.23), получаем:
d 2 b |
|
db |
|
|
q1q2 |
|
2 |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4 0mv |
2 |
tg |
3 |
/ 2 cos |
2 |
/ 2 |
|
||||
|
|
|
|
|
|
|
|
|
(2.24)
(2.25)
(2.26)
Подставляя в (2.26) формулу для телесного
угла
d 2 sin d 2 2sin 2 cos 2
получаем в окончательном виде формулу
Резерфорда (2.5):
d |
1 |
|
q1q2 |
|
2 |
d |
|
|
|
|
|
|
|
4 |
4 0mv |
2 |
sin4 |
|||
|
|
|
|
|||
|
|
|
|
|
|
2 |