Лекции / tfkp3

Конформные отображения, осуществляемые степенной, показательной и тригонометрическими функциями

В точке z=0 не выполнен условие критерия конформности - производная отлична от нуля отображение степенной функцией, как и любой другой, можно осуществлять просто отображая границы составили систему – действительная часть, мнимая часть, уравнение границы. Исключили х, у, получили уравнение образа.

Свойства

Когда кривая является окружностью с центром в начале координат или прямой проходящей через начало координат, запишем степенную функцию в показательной форме.

Из этих равенств следует, что окружности |z| = r комплексной плоскости (z) отображаются на окружности |w| = r^n плоскости (w).

Лучи arg z = а, выходящие из начала координат на плоскости (z) отображаются на лучи argw = nа плоскости (w), причем луч arg z = 0 отображается сам на себя argw = 0; то есть радиус надо возводить в степень n, а углы увеличивать в n раз.

Причем отображение не будет комформно во всей плоскости (область конформности - сектор – угол )

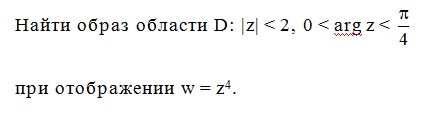
Примеры

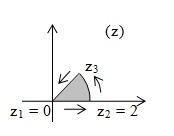
Граница области состоит из трех частей -все три относятся к линиям, которые можно отображать с помощью свойств окружность - центр в начале координат; лучи выходят из начала координат. Отображение будет конформно в любом секторе раствора 2*пи/4 = пи/2, наша область попадает в область конформности (если не попадает - то отображение не будет конформным - не будет взаимнооднозначности).

Функция w=z^4 отображает окружность |z| = 2 на окружность |w| = 16. Лучи argz = 0 и argz =пи/4 переходят соответственно в лучи arg w = 0 и arg w = пи.

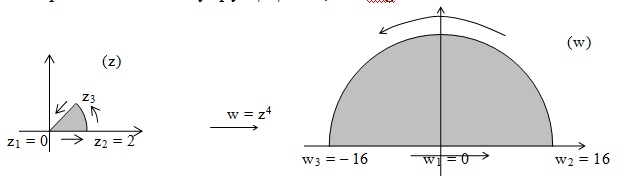
У нас граница исходной области - две полупрямые, их надо превратить в окружность .

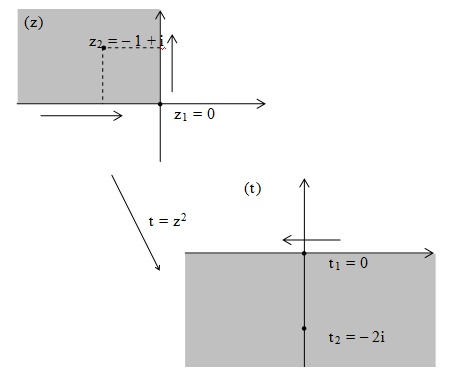Теперь у нас граница области прямая Im t =0, ее надо превратить в окружность, подобрав дробно-линейное отображение.

Точка t2 = – 2i должна, но при дробно-линейном отображении симметричные точки переходят в симметричные с центром круга симметричной является бесконечность; – 2i - переходит в центр, симметричная с ней относительно прямой в бесконечность, а симметричной будет 2i; чтобы 2i перешла в бесконечность надо чтобы она была особой, то есть знаменатель отображения (t-2i) перейти в центр круга.

Точка t₂ = – 2i должна перейти в центр круга, а центр у нас в 0, то есть точка t₂ = – 2i должна перейти в w₂=0, а точка t₁= 0 должна перейти в w₁=i, вот из этих условий и подбираем числитель записать отображение так w = (a+b*t)/(t-2i) и найти a,b

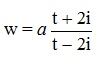
Показательная функция

Эта функция периодическая (период 2pi*i), отображение будет конформным в любой горизонтальной полосе шириной 2pi.

Из этих равенств следует, что вертикальные прямые х=а перейдут в окружности =е^а или |w|=exp(a); а горизонтальные прямые у=b перейдут в лучи  = b или argw = b.

То есть если у вас граница области содержит вертикальные или горизонтальные прямые - используем свойства, если другие линии, то составляем систему и исключаем х,у.

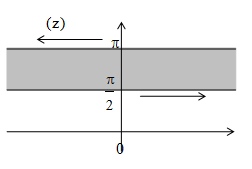Граница области - горизонтальные прямые, они переходят в лучи . Прямая у=пи/2 перейдет в луч arg w = pi/2;

Прямая у=пи перейдет в луч arg w = pi.

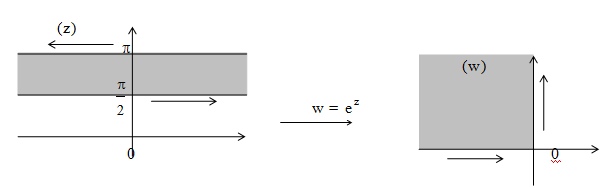
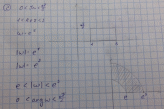Последние два предложения - это мы определили, какая область получается - отследив направление движения по границе.

Функция Жуковского

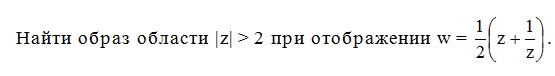
Внешность круга тоже в плоскость с разрезом, поэтому если исходная область лежит и в единичном круге, и вне его - взаимнооднозначность может быть нарушена.

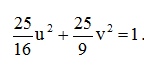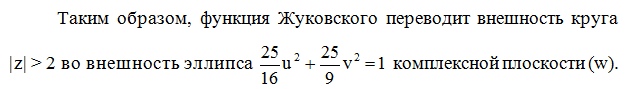С ледовательно, образом окружности |z| = 2 является эллипс с полуосями 4/5 и 3/5. Точка z = 5, принадлежащая области |z| > 2, переходит в точку w = 13/5.

Е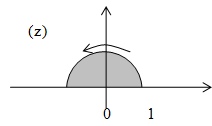 сли граница находится на единичной окружности или на осях координат, то можно обойтись без системы.

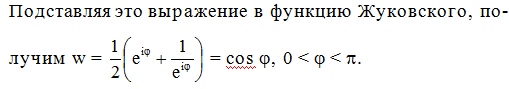Граница из двух частей - верхняя дуга единичной окружности и отрезок действительной оси. На полуокружности модуль равен 1, аргумент меняется от 0 до пи, отсюда такое уравнение в показательной форме.

Итак, верхняя полуокружность перешла в отрезок действительной оси, теперь надо разобраться с отрезком -1<x<1; на этом отрезке z=x поэтому w будет действительным.

И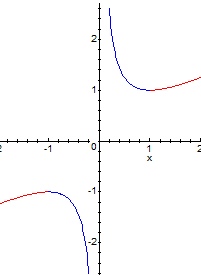 нтересующая нас часть выделена синим .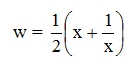

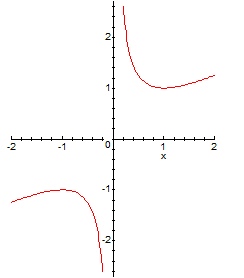
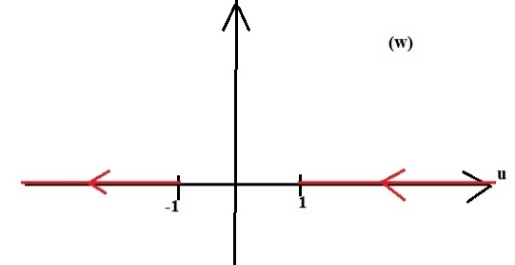К ак бы выходим из точки минус 1 и идем влево, доходим до бесконечности, и потом из бесконечности до 1 (по красной линии идем). Так как мы следили за направлением обхода, то и здесь область останется по левую руку, получается нижняя полуплоскость.

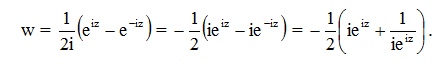Тригонометрические функции w = sinz и w = cosz могут быть представлены в виде суперпозиции линейной функции, показательной функций и функции Жуковского. С помощью формулы Эйлера функцию w = sinz можно представить в виде

Следовательно, отображение w = sinz сводится к последовательному выполнению преобразований, то есть чтобы выполнить отображение функцией w = sinz надо будет сделать 5 отображений.

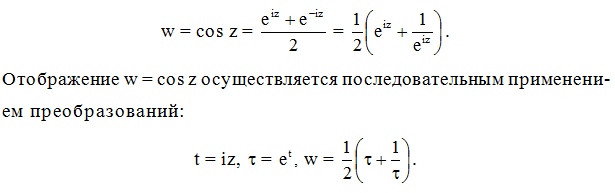
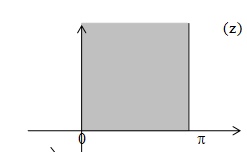
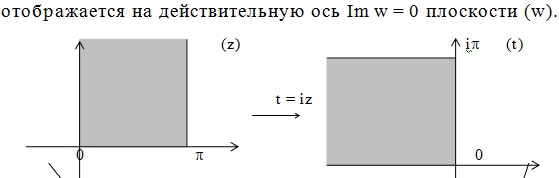
У вас граница - две горизонтальные полупрямые - они перейдут в части лучей и отрезок вертикальной прямой - он перейдет в дугу окружности.

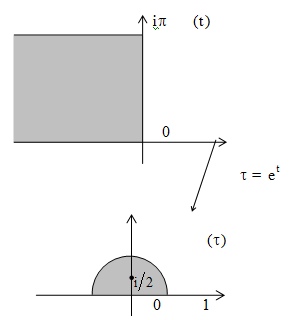
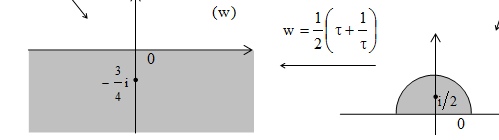
Точка i/2 на графике отмечена, чтобы показать, что полукруг перейдет в полуплоскость.