Лекции / tfkp5

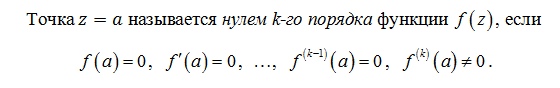
Найти нули и определить порядок приравниваем функцию к нулю и решаем уравнение

Получаются корни 0, 2i, -2i; теперь порядок нуля, в случае многочлена это просто разложили на множители и посмотрели степень скобки.

Z = 0 - нуль второго порядка; z = 2i, z = -2i - нули первого порядка

Теперь порядок нуля - на множители не разложить; для этого есть 2 способа

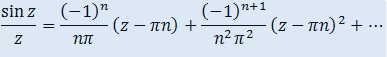
Разложить функцию в ряд Тейлора в окрестности 0, то есть в окрестности точек *n ряд будет по степеням (z-*n) Теперь выносим разность (z-*n) за скобку, так чтобы в скобке остался степенной ряд, сумма которого не равна нулю в точке *n.

В больших скобках при z=pi*n получается не 0, то есть мы вынесли множитель, из-за которого 0 получается скобка (z-pi*n) в первой степени значит это нули первого порядка.

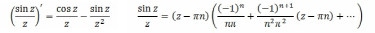Теперь 2 способ: он основан на нахождении производных, находим первую производную и подставляем точку.

Первая производная отлична от нуля значит это нуль первого порядка.

Пример. Определяем порядок, находим производную первая производная отлична от нуля, значит это нуль первого порядка.

То есть k₁ = 3, k₂ = 1, k₁ > k₂, следовательно особая точка z = 0 – устранимая.

Вычеты

То есть это интеграл по контуру, содержащему внутри точку в которой надо найти вычет.

Если точка особая, то внутри не должно быть других особых.

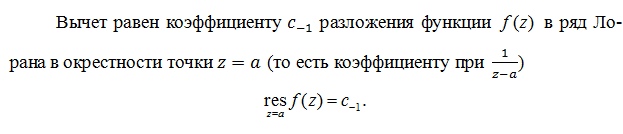Если сравнить определение вычета и формулы для вычисления коэффициента ряда Лорана, то окажется.

То есть вычет всегда можно найти как коэффициент разложения в окрестности данной точки, но это достаточно громоздкие расчеты, и если возможно, то стоит использовать другие формулы.

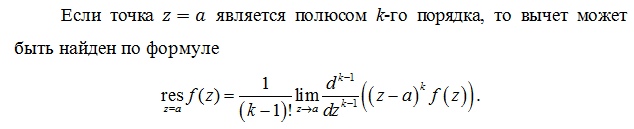
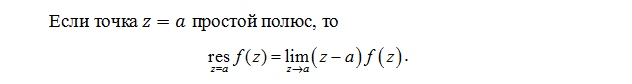В случае простого полюса (первого порядка) формула выглядит намного проще.

И для простого полюса есть еще одна.

Практика

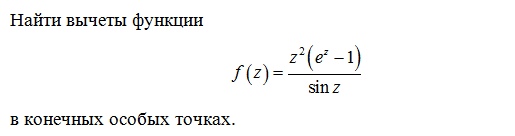1. Сначала находим все особые точки; определяем тип особой точки z=0 и особых точек z=*n, n<>0.

2. Устранимая особая точка:

Ноль - это когда нет особенности и точка правильная, то есть если получается ноль k-го порядка, но наша точка особая, поэтому классифицируете ее как устранимую.

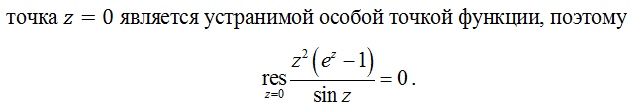
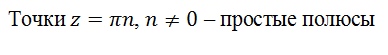3. *n – простой полюс; z = 0 – устранимая точка вычет всегда равен 0.

4. Т 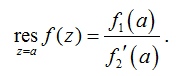еперь надо выбрать как найти вычет; но сначала надо проверить применимость формулы – выполнение всех условий.

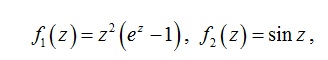
5. Ф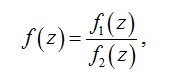 ункцию можно представить в виде

Числитель не равен 0, знаменатель равен 0, производная знаменателя не равна 0, это обязательные условия для использования формулы.

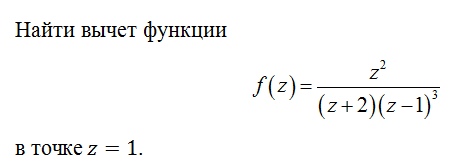М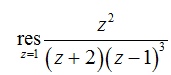 ожно было кратко так задачу записать

1) определить тип точки

2) выбрать формулу

3) вычислить вычет

Здесь нельзя сравнивать порядки числителя и знаменателя - особенность в аргументе функции - надо раскладывать в ряд Лорана в окрестности этой точки.

Установили, что главная часть ряда содержит ꝏ число слагаемых – точка существенно особая

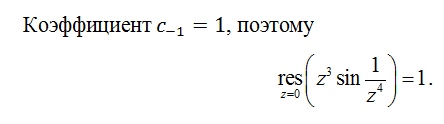
Тот же самый интеграл, но контур обходят по часовой стрелке, тогда бесконечность остается по левую руку – внутри области.

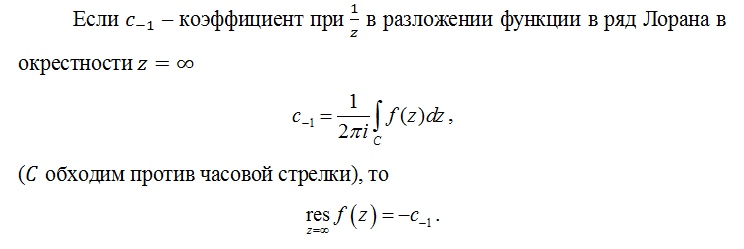За счет смены направления обхода появляется знак минус.

Практика 2

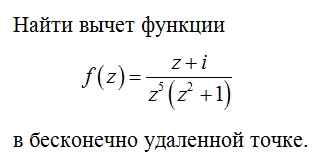З десь можно разложить в ряд Лорана по степеням z в окрестности бесконечности, но существует формула для вычисления вычета в бесконечно удаленной точке.

Но она используется только в устранимой бесконечно удаленной, когда можно доопределить функцию в точке - найти f (беск.). Итак, определяем тип точки. Меняете z на 1/дзета и определяте тип точки дзета =0.

Сравниваете порядки нуля дзета = 0 в числителе и знаменателе; знаменатель по сути вообще в 0 не обращается; дзета = 0 – нуль функции.

Значит можно считать точку z=0 правильной.

Но вычет в правильной бесконечно удаленной точке может быть отличен от 0, как и в устранимой.

Используем формулу

Подставляем в формулу

318, 319, 320, 321, 322, 323, 324, 325, 326; 331, 332, 333, 334, 335, 336, 337, 338; 366, 367, 368, 369, 370, 371