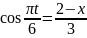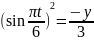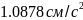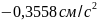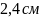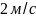Терлох / терлох(К1)

ЗАДАНИЕ К1

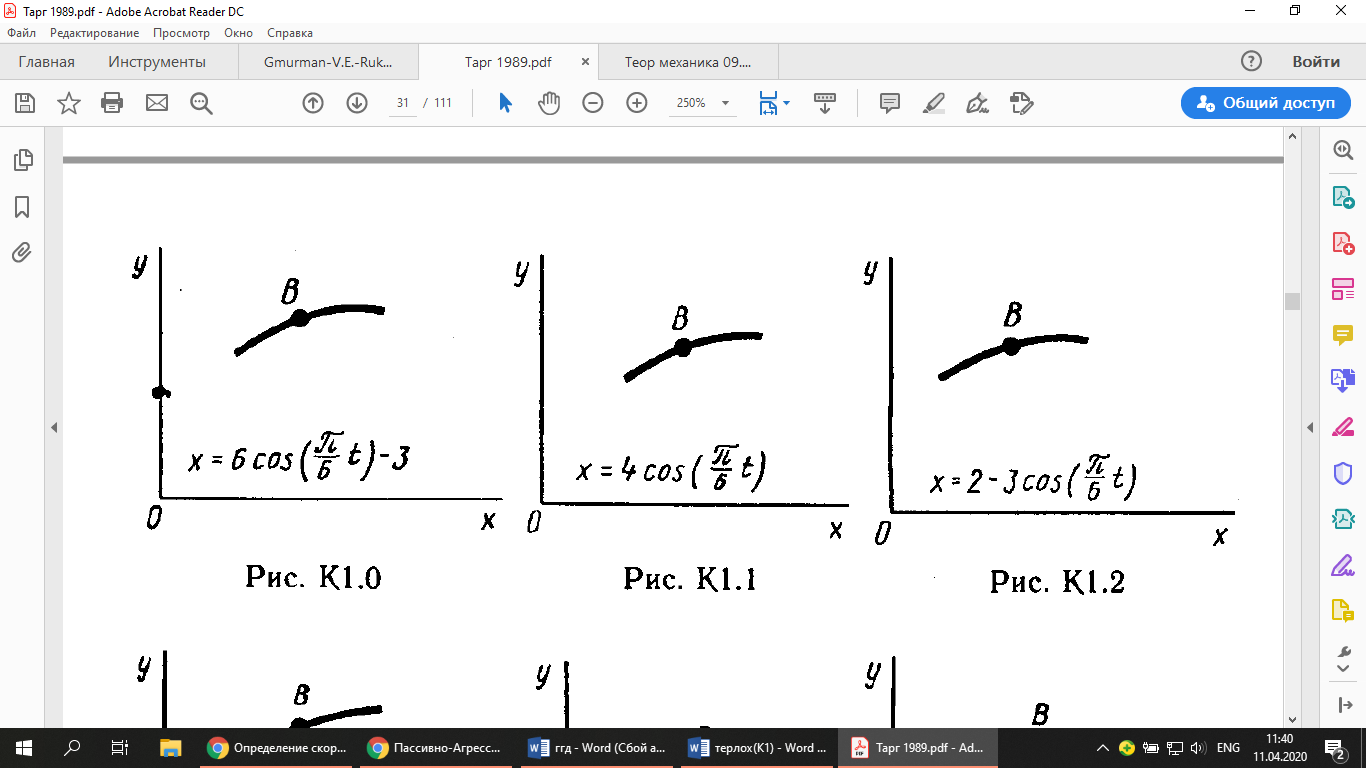Дано: , , , .

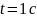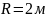Найти: уравнение траектории точки, , , .

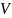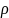Решение: (а)

1. Для определения уравнения траектории точки исключим из заданных уравнений движения время 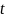. Поскольку входит в аргументы тригонометрических функций, где аргументы равны, используем основное тригонометрическое тождество

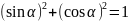(1)

Из уравнений движения находим выражения соответствующих функций и подставляем в равенство (1). Получим

следовательно,

Отсюда окончательно находим следующее уравнение траектории точки (параболы):

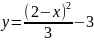
2. Скорость точки найдем по её проекциям на координатные оси:

и при

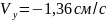
3. Аналогично найдем ускорение точки: (при )

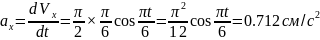
4. Касательные ускорения найдем, дифференцируя по времени равенство . Получим

откуда

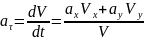
при 

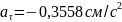
5. Радиус кривизны траектории 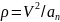. Подставляя сюда числовые значения и 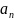, найдем, что при 

Ответ:

Решение: (б)

Определим скорость точки:

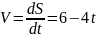
При получим

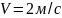
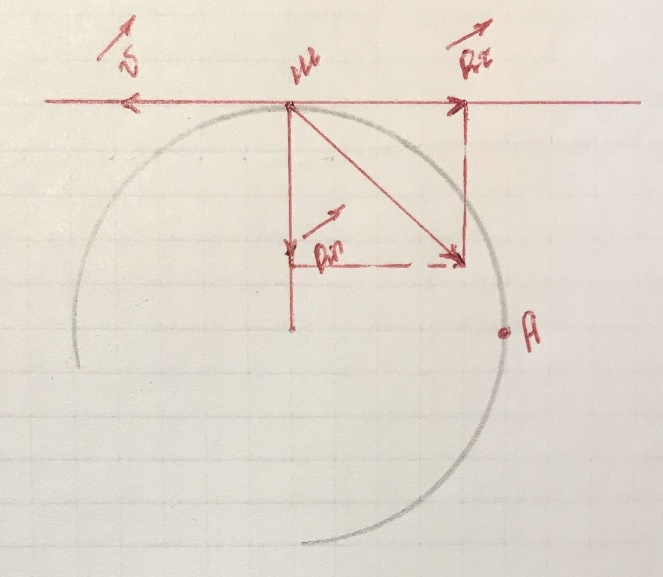
Ускорение находим по его касательной и нормальной составляющим:

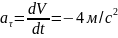
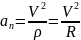
При получим, учтя, что ,

Тогда ускорение точки при будет

Ответ: