1.5.Давление насыщенных паров

Анализируя материал предыдущего раздела можно сформулировать другое определение давления насыщенных паров – это давление пара, находящегося в равновесии с жидкостью при данных термодинамических условиях и соотношении объемов фаз. Такая характеристика позволяет судить о склонности нефтей и нефтепродуктов к образованию паровых пробок, например в трубопроводе, потерях при испарении и хранении в резервуарах и т.д., и является основным показателем испаряемости и стабильности товарных нефтепродуктов.

(1.19)

Давление насыщенных паров р_S химически однородных жидкостей и азеотропных (не изменяющих свой состав в процессе испарения) веществ изучено достаточно хорошо. Установлено, что р_S зависит от температуры и может быть определено с помощью простой формулы:

где р_ST – давление насыщенных паров при температуре Т; р_STo – давление насыщенных паров при известной температуре Т_о; k – эмпирический коэффициент.

Таблица 1.8

Давление насыщенных паров алканов (р_АБС)

ºС	Давление, МПа
	С2Н5	С3Н8	i-С4Н16	С4Н10	i-С5Н10	C5Н10	С6Н14	С7Н16	С8Н18
-10	1,786	0,332	0,105	0,087	-	-	-	-	-
-5	2,040	0,392	0,125	0,082	0,041	-	-	-	-
0	2,308	0,448	0,150	0,100	0,033	0,023	0,003	-	-
5	2,502	0,332	0,179	0,121	0,051	0,029	-	-	-
10	2,922	0,617	0,211	0,143	0,075	0,036	0,010	0,003	0,001
15	3,253	0,711	0,247	0,171	0,062	0,046	0,012	0,004	-
20	3,672	0,817	0,289	0,197	0,105	0,055	0,016	0,005	0,002
25	4,051	0,934	0,334	0,238	0,089	0,066	0,020	0,005	-
30	4,504	1,050	0,386	0,274	0,145	0,079	0,024	0,008	0,003
35	4,795	1,204	0,443	0,318	0,125	0,084	-	0,010	-
40	tкип	1,353	0,508	0,365	-	0,112	0,037	0,012	0,004
29 45	-	1,527	0,579	0,420	0,171	0,131	0,040	0,015	-

Давление р_S паров индивидуальных углеводородов и нефтяных фракций можно определить, пользуясь различными графиками или например табл. 1.8.

(1.20)

Для смеси жидких углеводородов согласно закону Рауля давление насыщенных паров зависит от давления насыщенных паров отдельных компонентов и от мольных концентраций. Парциальное давление р_i любого компонента в жидкой смеси равно произведению давления насыщенного пара р_Si чистого компонента на его мольную концентрацию х_i в чистом виде, т.е. упругость паров жидкости равна сумме давлений компонентов этой смеси, которую они бы имели, если бы каждый занимал при данной температуре весь объем смеси, т.е. сумме парциальных давлений, или согласно закону Дальтона (1802 г.) парциальное давление р_i компонента, входящего в состав паровой фазы, равно произведению мольной концентрации компонента в паровой фазе на общее давление, т.е

(1.21)

р_i = р_Sy_i. (1.22)

Таким образом, из уравнений (1.21÷1.22) имеем

х_iр_Si = р_Sy_i. (1.23)

Уравнение (1.23) известно под названием объединенного закона Дальтона – Рауля, согласно которому можно сделать важный вывод – в состоянии равновесия парциальное давление любого компонента смеси в паровой фазе равно парциальному давлению того же компонента в жидкости.

Из приведенного уравнения следует, что

р_Si/p_S = y_i/x_i = k_i = const

или

р_Si = k_piр_S и y_i = k_pix_i. (1.24)

Коэффициент k_рi, который называют константой равновесия, у отдельных компонентов зависит от температуры и давления и определяется, как правило, из специально составленных графиков. Приведенные уравнения позволяют, например, найти состав газовой фазы по известному составу жидкостей и наоборот.

Константы равновесия (в зарубежной литературе больше известны как константы фазового распределения) дают возможность прогнозировать материальный баланс многокомпонентных двухфазных систем (концентрации компонентов в разных фазах) при условии, если заданы давление и температура и известна также молярная концентрация i-го компонента в однофазном состоянии x_i⁰.

30

Для любого компонента число молей в двух фазах определяется как сумма N_i^г и N_i^ж, т.е. N_i⁰ = N_i^г + N_i^ж. Отсюда молярная концентрация:

x_i⁰ = у_iг + х_iж,

где г и ж – числа, показывающие соответственно, какая доля общего количества молей находится в газообразном и жидком состоянии (г + ж= 1).

На практике при расчете ж используют метод последовательного приближения, легко реализуемого с помощью персонального компьютера. При этом полагают, что  x_i = 1.

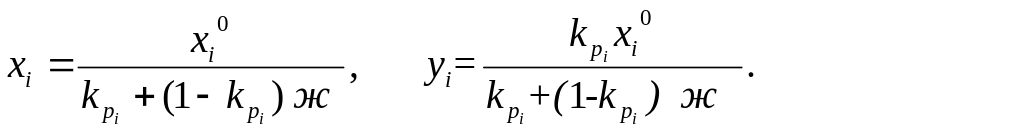Учитывая, что у_i/x_i = 1, можно получить следующее выражение для концентрации i-го компонента в жидкой и газообразной фазах:

а) для жидкой фазы:

б) для газообразной фазы:

В двухкомпонентной системе равновесные составы могут быть определены значительно проще.

Приоритет в исследовании констант фазового равновесия углеводородов принадлежит американскому нефтяному институту АРJ, диаграммы которого широко используются в нефтепереработке. Известна также методика NGPSA, позволяющая определить значение k_р при температурах, достигающих 430С. Опубликованные в печати варианты этих методик весьма сложны и неудобны для практического использования, а варианты компьютеризации схем являются собственностью разработчиков: Тодда, Лесли, Доулинга, Сталла, Соавва, Шервуда и др. Можно отметить публикации отечественных авторов: А.И. Гриценко, Г.Р. Гуревича, В.П. Мамуны, Т.Д. Островского, Г.М. Ярышева, и др. В Сибирском научно-исследовательском институте (СибНИИНП) Шиловым В.И. впервые экспериментально подтвержден метод определения k_p в зависимости от молекулярной массы различных нефтей Западной Сибири применительно к условиям нефтепромыслов с высокими значениями абсолютного давления со средней погрешностью 13,8%. Максимальное отклонение 44% установлено для нормального октана.

Д

31

аже при низких давлениях и температурах константы равновесия мало зависят от состава смеси, а постоянными их можно считать при фиксированных давлениях и температуре и лишь для идеальных растворов. В настоящее время в России накоплен достаточно большой экспериментальный материал, однако значение константы k_iр можно использовать в расчетах парожидкостного равновесия только для систем, адекватных лабораторным. Последнее условие в значительной степени снижает достоинства такой информации в условиях постоянного изменения составов фаз, имеющих место, например при испарении нефтей с открытой поверхности. Расчетные методы основаны на использовании уравнений реальных газов и могут быть весьма полезными.

при статистической обработке большого объема информации в ТюмГНГУ были разработаны методики расчета коэффициента k_p при низких давлениях (0,10,2 МПа) и температурах от 273 до 330 К. Для алканов получена зависимость

lg k_p = 6,8 – 2,7n_H + (2000 + 540n_H)T^-1 – р/р_ат, (1.25)

для алкенов и аренов рекомендуется следующая формула

lg k_p = 6,8 - 2,7n_H + 1990[1 + 0,302n_H – 9,95(n_H - n_HФ)n_НФ^-1]T^-1 – р/р_ат (1.26)

где n_H – число атомов водорода у алканов; n_НФ – число атомов водорода у нафтенов (цикланов) или у аренов; р и р_ат – абсолютное и атмосферное давление, соответственно.

В предложенных уравнениях (1.25, 1.26) впервые использован количественный состав водорода, определяющий, по мнению авторов, летучесть нефтяной фракции или конденсата. Это предположение в значительной степени упрощает соответствующие расчеты по сравнению с зарубежными аналогами.

Закономерность изменения коэффициентов фазового распределения компонентов k_рi от температуры системы t, заданная с помощью экспериментальных данных, оказалась близкой к экспоненциальной

. (1.27)

32

Для нахождения коэффициентов A_i и C_i разработаны программы на ПЭВМ, реализующая вышеописанный метод нелинейной регрессии. Использование разработанного алгоритма оказалось весьма удобным и эффективным при обработке автором настоящей работы результатов последующих аналогичных экспериментальных исследований, описанных в следующих главах. В качестве примера в табл. 1.9 приведены значения коэффициентов полученной зависимости (1.27) для чистых компонентов смеси.

Таблица 1.9

Значения коэффициентов для чистых углеводородов

Коэффи-циенты	Компонент cмеси
	CH4	C2H6	C3H8	iC4H10	C4H10	IC5H12	C5H12	C6H14
Аi	127,14	17,31	4,55	1,57	1,08	0,32	0,24	0,055
Сi	0,324	0,529	0,622	0,757	0,811	0,973	1,027	1,270

Закономерность изменения коэффициентов фазового распределения k_рi узких фракций от температуры системы t, также близка к экспоненте и удовлетворительно аппроксимируется следующей функцией:

, (1.28)

где t_К – средняя температура кипения фракции, С.

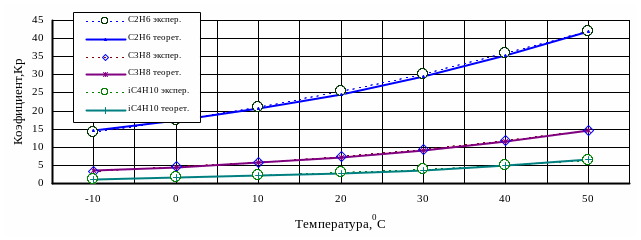
регрессионные модели (1.27), (1.28) адекватны по критерию Фишера и характеризуются малой погрешностью расчета (не более 5÷15%) с коэффициентом множественной корреляции R = 0,97. В качестве примера для ряда углеводородов на рис. 1.7 показано графически отклонение расчетных значений коэффициента фазового распределения k_рi от экспериментальных.

С повышением температуры и общего давления давление насыщенных паров отдельных компонентов смеси существенно увеличивается, дополнительно характеризуя отклонение от идеального газа. Таким образом, в уравнения, характеризующие состояние и соотношения паровоздушной среды, Л.Г. Льюисом (1901 г.) была введена величина фугитивность f, значение которой приближается к давлению насыщенных паров при бесконечном уменьшении последней, т.е.

(1.29)

В ряде случаев целесообразно использовать соотношение фугитивности и давления насыщенных паров, называемое коэффициентом активности вещества а_Ф (в зарубежной литературе часто встречается под названием коэффициента летучести):

Коэффициент фугитивности показывает, во сколько раз фугитивность больше давления насыщенных паров и более точно выражает стремление вещества переходить из жидкой фазы в паровую. Для инженерных расчетов обычно используют зависимость а_Ф от приведенных р_ПР и Т_ПР.

33

Рис. 1.7. Отклонение расчетных значений коэффициента фазового распределения от экспериментальных

34

Рис. 1.7. Отклонение расчетных значений коэффициента фазового распределения k_рi от экспериментальных значений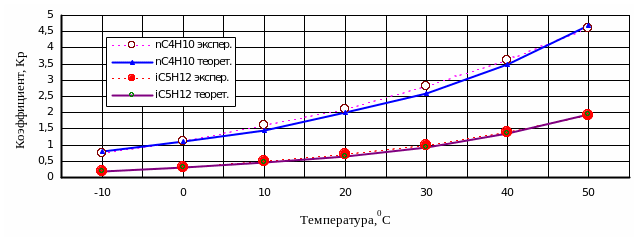

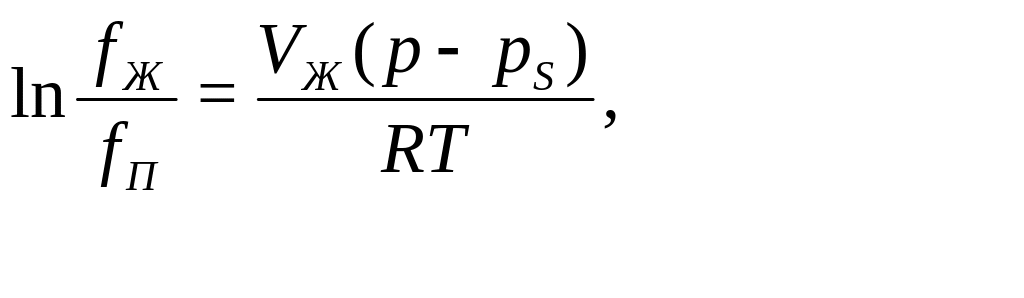При отсутствии равновесия отношение фугитивности жидкости к фугитивности пара можно определить по уравнению

где f_Ж – фугитивность компонента в чистом виде при давлении р и температуре Т; f_П – фугитивность компонента при давлении насыщенного пара; р – давление смеси; р_S – давление насыщенных паров компонента.

К понятию фугитивности легко прийти путем анализа уравнений состояния идеального газа при постоянной температуре:

Vdр = RT d(ln р) = RT d(ln f).

Когда величина объема известна как функция давления или определена непосредственным измерением или расчетным путем по уравнениям состояния, изменение фугитивности можно установить путем интегрирования:

Т.к. а_Ф = 1 при р = 0, то можно определить абсолютное значение коэффициента фугитивности:

Таким образом, очевидно, что интегрируемая функция представляет собой отклонения от поведения идеального газа и при р = 0 также стремится к нулю.

Ф

35

азовые превращения (переход из жидкого состояния в газообразное) в условиях транспорта и хранения таких многокомпонентных веществ, как нефть и нефтепродукты, вследствие исключительной сложности их состава протекают значительно сложнее, чем химически однородных веществ. В процессе испарения постепенно испаряются более легкие фракции, в результате чего жидкая фаза утяжеляется. Таким образом, в течение процесса изменяются и парциальные давления индивидуальных углеводородов, общее давление насыщенного пара нефтепродуктов всегда выше на 1030%, чем следовало бы ожидать из закона аддитивности. Напомним, что аддитивность – свойство ряда химических веществ, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям. Например, масса вещества равна сумме масс его компонентов.

(1.31)

Давление р_S паров моторных топлив при нормальных условиях t = 0ºC можно определить по известной формуле Г.Ф Большакова:

где t_К – средняя температура кипения, ºС.

В интервале температур от –30 до +100ºС можно использовать формулу П.А. Рыбакова:

р_St = р₃₈ · 10^4,6-1430/T, мм. рт. ст. (1.32)

или следующую зависимость Г.Ф. Большакова:

lg р_S = B – A/T, (1.33)

где р_S – давление насыщенных паров, Па; А и В – коэффициенты.

При определении давления насыщенных паров нефтей и нефтепродуктов на практике необходимо учитывать два случая:

• когда объем паровой фазы V_П по сравнению с объемом жидкой фазы V_Ж невелик, можно считать, что в состоянии насыщения состав жидкой фазы не меняется и что последняя находится в равновесии с насыщенным паром;

• когда V_П значительно больше V_Ж, испарение наиболее летучих компонентов продукта приводит к изменению состава жидкости и в состоянии насыщения пар находится в равновесии с жидкостью, но уже измененного состава. Давление пара в этом случае будет отличаться от давления пара, определенного для небольшого объема V_П и будет тем больше, чем меньше соотношение V_П/V_Ж.

Давление р_S при объеме паровой фазы, близком к нулю, принимает максимальное значение и определяется давлением паров наиболее легких углеводородов:

Т аким образом, при характеристике давления насыщенного пара нефтепродуктов или нефтей необходимо указывать кроме температуры и соотношение объемов V_П и V_Ж, при котором проведены следующие соответствующие измерения р_S. При решении инженерных задач выбор соотношения V_П/V_Ж (при котором следует определять р_S) должен исходить из конкретных производственных условий. Особенно это важно для таких случаев, когда V_П/V_Ж   и пары далеки от насыщения, или когда V_П/V_Ж  0 и давление насыщенных паров имеет максимальное значение.

З

36

ависимость давления насыщенных паров нефтяных топлив от соотношения фаз с достаточной точностью описывается формулой Н.И. Тихонова:

Известно аналогичное уравнение для определения р_S в резервуаре:

р_S = 1,29(t/38)^0,69(V_Ж/V)^0,19р_S38, (1.34)

где t – температура поверхности жидкости.

На практике давление насыщенных паров обычно определяется различными методами:

• методом Рейда, заключающимся в регистрации по манометру избыточного давления насыщенных паров нефтепродуктов, помещенном в специальную «бомбу» и нагретым до 37,8ºС (38ºС), причем соотношение жидкой и паровой фаз в бомбе Рейда составляет 1:4 (ГОСТ 1756-52);

• методом Валявского-Бударова, основанным на определении изменения объема паров смеси при нагреве нефтепродуктов до 37,8ºС в стеклянном приборе, при этом соотношение жидкой и паровой фаз принято равным 1:1.

В настоящее время известно значительное количество работ: Ф.Ф. Абузовой, И.С. Бронштейна, Л.Р. Хакимьяновой, Д.М. Саттаровой, В.Ф. Новоселова, А.А. Коршака и других специалистов ВНИИ НП, ГрозНИИ, БашНИИ, МИН и ГП, ВНИИгаз, УНИ, УфНИИ, ТПИ и др., в которых на достаточно высоком уровне изучены давления насыщенных паров различных нефтепродуктов и нефтей. Отмечается, например, несовершенство, длительность, трудоемкость, плохая сходимость результатов изменения р_S по методу Рейда. Точность метода невысока, расхождения между параллельными определениями составляют около 4 кПа, на что влияет отбор и заправка бомбы, квалификация персонала, время года и т.д. Величины давления насыщенных паров, определенные по методу Рейда, обычно на 0,0080,01 МПа ниже значений, полученных по методу Валявского-Бударова.

Следует отметить, что в процессе хранения нефтепродуктов величина соотношения жидкой и паровой фаз может меняться от бесконечности (при хранении в резервуаре с плавающими крышами или понтонами, когда практически отсутствует паровая фаза) до нуля при полной откачке нефтепродукта из резервуара. Так, для автомобильных бензинов при отношении объема жидкой фазы к паровой 10:1 (при заполнении резервуаров на 90%) давление насыщенных паров может быть в 2 раза больше, чем при заполнении резервуара на 10% (отношение фаз 1:10).

У

37

совершенствованный метод экспериментального определения давления насыщенных паров нефтей, летучих невязких нефтепродуктов и моторных топлив установлен ГОСТом 28781-90. Особенность этого метода состоит в предварительном диспергировании анализируемой пробы в аэрозольное состояние (с использованием аппарата механического диспергирования типа «Вихрь»).

(1.35)

Расчетное определение давления р_S (в МПа) насыщенного пара жидких углеводородных смесей по ГОСТ 28656-90 осуществляется при фиксированной температуре, исходя из известного компонентного состава и фугитивности компонентов смеси. Используется следующая приближенная формула:

где x_i и f_i – содержание и фугитивность i-го компонента в жидкой среде, соответственно.

Поскольку фугитивности компонентов заметно зависят от общего давления в системе, то расчет по этой формуле проводят итерационно. В обсуждаемом стандарте приведены подробные таблицы фугитивности чистых компонентов сжиженного газа при разных температурах и давлениях.

Давление р_S у различных нефтепродуктов по Рейду колеблется в следующих пределах (в Па): автобензин – до 9,33·10⁴, авиабензин – до 4,8·10⁴, керосин – 0,4·10⁴0,8·10⁴, дизельное топливо – 0,08·10⁴0,13·10⁴.

В

38

работах Ф.Ф. Абузовой, И.С. Бронштейна для бензинов уфимских нефтеперерабатывающих заводов установлен более широкий диапазон изменений р_S38, от 86 кПа до 126 кПа. В некоторых опытах р_S38 достигало примерно 149 кПа, а закипание нефтей в резервуарах и транспортных емкостях отмечалось при температурах ниже температуры начала кипения, определенной по ГОСТ 2177-66 и принятой за единицу стабильности. В трубопроводном транспорте стабильность нефтей ограничена условиями поставки, согласно которым р_S38 не должно превышать 66650 Па. Тем не менее, в реальных условиях эксплуатации нефтепроводов с малым объемом газовой фазы следует ожидать более высоких значений давления равновесия, что очень важно при производстве аварийно-восстановительных работ.

И

39

сследования, проведенные под руководством профессора Н.Н. Константинова, а позднее сотрудниками кафедры теплотехники Уфимского нефтяного института под руководством Ф.Ф. Абузовой показывают, что давление насыщенных паров нефтей в большей степени зависит от соотношения газовой и жидкой фаз. На рис. 1.10 по кривым равновесного состояния можно определить значение р_S38 при температуре, например 20ºС. Следует обратить внимание на то, что р_S при соотношении Vп/Vж = 0,1 превышало давление, лимитированное техническими условиями на нефть. Более того, при соотношении Vп/Vж, близком к нулю, давление насыщенных паров превышает нормируемое практически во всем диапазоне положительных температур. Данный факт еще раз объясняет наблюдающееся повышение давления в трубопроводе при производстве аварийно-восстановительных работ, обусловленных нарушением герметичности линейной части. Температура начала кипения бензинов также не всегда является определяющим фактором величины давления насыщения, что для нефтей и конденсатов может быть значимо.

Давление насыщенных паров р_S характеризуется также величиной потерь σ углеводородов, испарившихся из первоначального объема. Но потери от испарения нефтей, имеющих одинаковую исходную и конечную упругость паров, различны и зависят от углеводородного состава.

При уменьшении упругости паров с 1180 мм. рт. ст. до 450 мм. рт. ст. (при 38ºС) потери нефти Кулешовского месторождения составляют 4, Ромашкинского – 2, Усть-Балыкского – всего 0,25%. Поэтому для определения давления насыщенных паров необходимо априори знать зависимость р_S = ƒ(σ) для каждой нефти. В случае, когда экспериментальным путем найдена величина р_S при потере вещества σ, давление насыщенных паров при той же температуре и при любом значении σ_i можно рассчитать по формуле

р_Si = р_S e ^{–k(σi- σ)} . (1.36)

Здесь следует напомнить, что если смесь не является постоянно испаряющейся, то величина давления данных компонентов над смесью будет также изменяться. Зависимость р_S от температуры для разных нефтей также неодинакова. Для точных расчетов необходимо еще знать зависимость р_S от температуры для каждого вещества.

Экспериментальные исследования показывают УфНТУ, что значение p_S при заданной температуре для различных сортов нефтепродуктов и даже для разных образцов одного нефтепродукта значительно различаются и не могут быть точно рассчитаны по стандартным физико-химическим показателям, хотя при расчете потерь от испарения в резервуарах при относительно небольших уровнях потерь σ = 10,5% весовых параметр p_S является одним из основных. В условиях испарения нефтей с открытой поверхности, когда объем паровой фазы бесконечно превосходит объем жидкой фазы, пары далеки от насыщения.

Целесообразно заметить, что стандартизованный метод определения давления насыщенных паров по ГОСТ 28656-90 в силу предельного упрощения расчетной схемы также оказывается не очень точным. Поэтому в настоящее время лучше использовать более строгие расчетные методы, основанные на современных уравнениях состояния многокомпонентных смесей. Таким образом, исходя из сказанного выше, для определения потерь нефтей от испарения с открытой поверхности использование давления насыщенных паров в качестве исходной характеристики представляется не корректным.

Для расчета давления насыщенных паров чистых углеводородов рекомендуется использовать известную формулу Антуана:

г

40

де Ai, Bi, Ci – коэффициенты в табл. 1.3.

Давление насыщенных паров конденсатов с известным углеводородным составом можно определить по следующей зависимости:

где k_Р – эмпирический коэффициент; x_i – концентрация углеводорода в конденсате.

Результаты исследований p_S стабильных и деэтанизированных конденсатов по методу Рейда, представленные на рис. 1.10, указывают на значительный разброс данных, особенно для деэтанизированного конденсата, что легко объясняется различным составом в конденсатах легких углеводородов. При известной концентрации легких углеводородов в конденсатах экспериментальные значения p_S удовлетворительно аппроксимируются следующей зависимостью:

(1.38)

где р_Si, x_i – парциальное давление и концентрация i-го компонента, k_S – коэффициент, характеризующий отклонение формулы (1.38) от закона аддитивности. Для исследованных стабильных конденсатов k_S = 1,3, для деэтанизированных k_S = 1,15.

Таблица 1.10

Значения коэффициентов Антуана

Углеводороды	А	Б	С	От Т	до Т
С2Н6	9,5784	1030,628	39,083	244	305
С3Н8	9,4337	1048,900	5,610	232	301
n-С4Н8	9,1181	1030,340	-22,190	272	348
i-С4Н8	9,3117	1120,165	-1,297	252	407
n-С5Н10	8,9995	1075,820	-39,791	244	393
i-С5Н10	8,9345	1020,010	-40,053	244	737
С6Н10	9,0026	1171,530	-48,784	214	423

В заключение следует отметить, что давление насыщенных паров не следует путать с давлением насыщения, которое соответствует моменту появления первых пузырьков газа из газонасыщенной нефти при понижении давления. Как правило, абсолютное значение давления насыщенных паров значительно меньше давления насыщения, которое, например, для пластовых нефтей обычно составляет 1,2÷9,0 МПа.