
1-1 Основы теории цепей / ПЗ-3
.docxПЗ3: РОЗРАХУНОК КІЛ ПРИ ГАРМОНІЙНИХ ВПЛИВАХ. СИМВОЛІЧНИЙ МЕТОД
5.1 Мета заняття
Закріплення теоретичних знань за темою "Основні положення символічного методу аналізу ЛЕК". Одержання навичок з розрахунку частотних характеристик ЛЕК. Набуття навичок аналізу і розрахунку розгалужених кіл при гармонійному впливі, навичок зображення векторних діаграм і їхнього аналізу.
5.2 Контрольні запитання та завдання
Що таке гармонійне коливання і які його параметри? Зіставлення фаз гармонійних коливань.
Представлення гармонійних коливань за допомогою векторів.
Додавання гармонійних коливань однакових частот.
Які співвідношення між амплітудами і початковими фазами гармонійних коливань струму і напруги на затискачах R-, L- і С- елементів?
Яка мета введення в теорію кіл символічного методу?
Представлення комплексних чисел у різних формах; сполучені комплексні числа; формула Ейлера.
Приведіть правил виконання дій над комплексними числами (додавання, вирахування, множення і розподіл).
Сформулюйте закони Кірхгофа і закон Ома для комплексних амплітуд напруг і струмів.
Комплексні опори і провідності двополюсників.
Яка послідовність розрахунку кіл символічним методом?
Що таке комплексні передатні функції? Амплітудно-частотні і фазо-частотні характеристики (АЧХ і ФЧХ) кола.
Як провадиться розрахунок розгалужених кіл символічним методом?
Зображення комплексних чисел на комплексній площині.
Додавання, вирахування векторів на комплексній площині.
Яке взаємне розташування векторів струму і напруги на затискачах R-, L- і С- елементів?
Наведіть формули розрахунку миттєвої, активної, реактивної і повної потужності гармонійних коливань.
Як провадиться розрахунок комплексної потужності?
5.3 Приклади розв'язання задач
Задача 1. Маємо
коло 1-го порядку рис. 5.1. На вхід кола
подається гармонійний сигнал
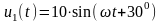 В,
R=2 Ом,
С=30 мкФ,
В,
R=2 Ом,
С=30 мкФ,
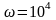 рад/с.
Знайти струм у колі і сигнал на виході
кола
рад/с.
Знайти струм у колі і сигнал на виході
кола
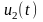 .
Зобразити АЧХ і ФЧХ кола.
.
Зобразити АЧХ і ФЧХ кола.
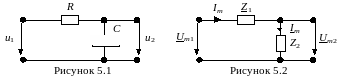
Розв'язок. Зобразимо схему кола з
комплексними опорами елементів
(рис. 5.2). Для цього кола
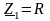 і
і
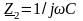 .
.
Комплексний вхідний опір кола
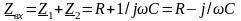 .
.
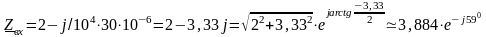 Ом.
Ом.
Комплексна
амплітуда вхідного сигналу
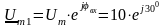 В.
В.
Комплексна амплітуда струму в колі
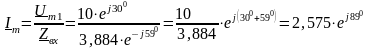 А.
А.
Комплексна амплітуда вихідного сигналу
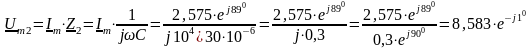 В.
В.
Переходячи від комплексних амплітуд
до миттєвих значень, одержуємо струм у
колі і напругу на виході кола:
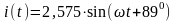 А,
А,
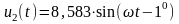 В.
В.
Комплексний коефіцієнт передачі кола,
що представляє із себе дільник напруги
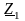 і
і
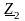 (рис. 5.2), знаходиться так:
(рис. 5.2), знаходиться так:
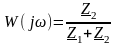 .
Тоді
.
Тоді
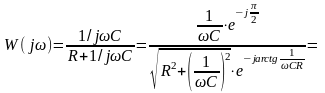
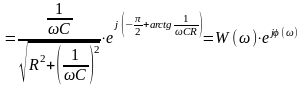 ,
,
де
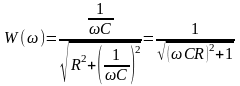 - амплітудно-частотна характеристика
(АЧХ);
- амплітудно-частотна характеристика
(АЧХ);
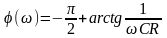 - фазо-частотна характеристика (ФЧХ).
- фазо-частотна характеристика (ФЧХ).
Провівши нескладний аналіз функцій
однієї перемінної
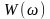 і
і
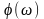 ,
зобразимо графіки АЧХ і ФЧХ.
,
зобразимо графіки АЧХ і ФЧХ.
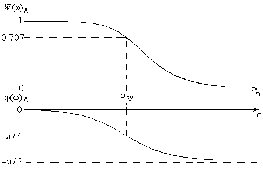
Рисунок 5.3
Відповідь: А, В.
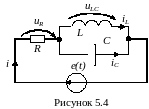
Задача 2.
Розрахувати комплексні амплітуди
струмів у вітках і напруг на елементах
для схеми рис. 5.4, якщо
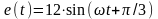 В,
R= 30 Ом,
С=
10 мкФ, L=
0,3 мГн,
В,
R= 30 Ом,
С=
10 мкФ, L=
0,3 мГн,
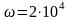 рад/с.
Зобразити векторну діаграму всіх струмів
і напруг.
рад/с.
Зобразити векторну діаграму всіх струмів
і напруг.
Розв'язок. Визначимо комплексний опір ємності й індуктивності:
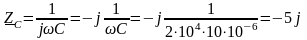 Ом;
Ом;
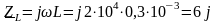 Ом.
Ом.
Комплексний опір усього кола
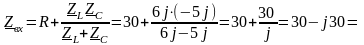
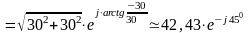 Ом.
Ом.
Фаза
джерела ЕРС у градусах
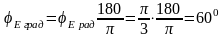 .
.
Комплексна
амплітуда ЕРС
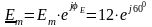 В.
В.
Комплексна амплітуда струму в колі
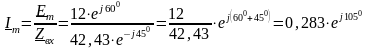 А.
А.
Для знаходження струму в індуктивності й у ємності скористаємося формулою дільника струму
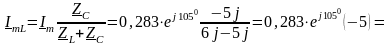
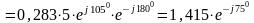 А.
А.
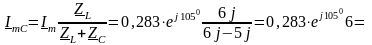
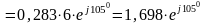 А.
А.
Комплексні амплітуди напруг на елементах знайдемо за законом Ома
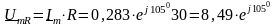 В.
В.
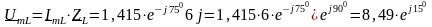 В.
В.
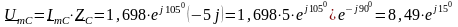 В.
В.
Як видно,
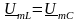 ,
що очевидно, тому що індуктивність і
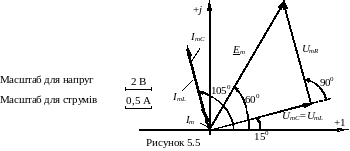
ємність з'єднані паралельно. Зобразимо
векторну діаграму (рис. 5.5). Для цього
необхідно вибрати масштаб для струмів
і напруг та на комплексній площині
відкласти вектора відповідної довжини
(амплітуди) і під відповідним кутом до
дійсної осі (початкові фази).
,
що очевидно, тому що індуктивність і
ємність з'єднані паралельно. Зобразимо
векторну діаграму (рис. 5.5). Для цього
необхідно вибрати масштаб для струмів
і напруг та на комплексній площині
відкласти вектора відповідної довжини
(амплітуди) і під відповідним кутом до
дійсної осі (початкові фази).
5.4 Варіанти задач
5.4.1 Маємо
коло 1-го порядку рис. 5.5
– 5.7. На вхід кола подається
гармонійний сигнал
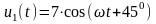 В. Визначити амплітуду і фазу вихідного
сигналу
фільтра
на частоті
В. Визначити амплітуду і фазу вихідного
сигналу
фільтра
на частоті
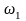 =
2
=
2
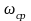 (
- частота зрізу фільтра). Зобразити АЧХ
і ФЧХ кола.
(
- частота зрізу фільтра). Зобразити АЧХ
і ФЧХ кола.
5.4.2 Для схем рис. 5.8 – 5.11 розрахувати комплексну передатну характеристику кола за напругою і зобразити АЧХ кола з указівкою характерних точок.
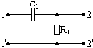
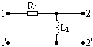
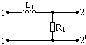
Рисунок 5.5 Рисунок 5.6 Рисунок 5.7
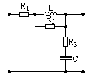
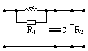
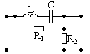
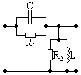
Рисунок 5.8 Рисунок 5.9 Рисунок 5.10 Рисунок 5.11
5.4.3 Для
схем рис. 5.12
– 5.14
розрахувати струм
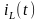 через індуктивність L
і напругу
через індуктивність L
і напругу
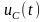 на ємності C,
якщо
на ємності C,
якщо
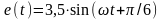 В,
R1=1
Ом, R2=1 Ом,
R3=3
Ом, С=
20 мкФ, L=
0,2 мГн,
рад/с.
В,
R1=1
Ом, R2=1 Ом,
R3=3
Ом, С=
20 мкФ, L=
0,2 мГн,
рад/с.
5.4.4 Якісно
зобразити векторну діаграму всіх струмів
і напруг для схем рис. 5.12 – 5.14, якщо
R2=R3,
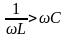 (рис. 5.12),
(рис. 5.12),
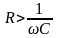 (рис. 5.13) і
(рис. 5.13) і
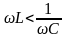 (рис. 5.14).
(рис. 5.14).
5.4.5 Розрахувати
струми у вітках і напруги на елементах
для схем рис. 5.12
– 5.17, якщо
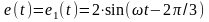 В,
В,
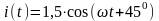 А,
R1=1 Ом,
R2=1 Ом,
R3=3 Ом,
С= 10 мкФ,
L= 0,3
мГн,
рад/с.
Зобразити векторну діаграму всіх струмів
і напруг.
А,
R1=1 Ом,
R2=1 Ом,
R3=3 Ом,
С= 10 мкФ,
L= 0,3
мГн,
рад/с.
Зобразити векторну діаграму всіх струмів
і напруг.
5.4.6 Розрахувати
комплексні амплітуди струмів у вітках
і напруг на елементах для схем рис. 5.8
– 5.11, якщо до входу кола
прикладена ЕРС
В,
R1 =
30 Ом, R2
= 20 Ом,
С =
15 мкФ, L =
0,4 мГн,
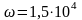 рад/с.
Зобразити векторну діаграму всіх струмів
і напруг.
рад/с.
Зобразити векторну діаграму всіх струмів
і напруг.
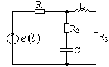
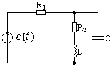
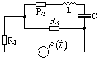
Рисунок 5.12 Рисунок 5.13 Рисунок 5.14
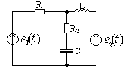
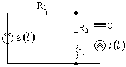
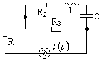
Рисунок 5.15 Рисунок 5.16 Рисунок 5.17
РЕЗОНАНСНІ ЯВИЩА В ЕЛЕКТРИЧНИХ КОЛАХ. РЕЗОНАНСНІ ЧАСТОТНІ ХАРАКТЕРИСТИКИ
6.1 Мета заняття
Набуття навичок аналізу і розрахунку коливальних контурів, навичок по використанню властивостей цих контурів у задачах фільтрації.
6.2 Контрольні запитання та завдання
Які умови резонансу напруг і струмів?
Зобразіть векторні діаграми струмів і напруг для випадків ємнісного, індуктивного й активного опорів контуру (послідовного, рівнобіжного).
Наведіть частотні характеристики рівнобіжного контуру (залежності вхідних опорів, струмів і напруг від частоти).
Наведіть частотні характеристики послідовного контуру.
Які відмінності ідеального контуру від реального?
Добротність контуру (послідовного, рівнобіжного).
Наведіть характеристики ідеальних фільтрів.
Що таке смуга пропущення контуру і який її зв'язок з добротністю?
Абсолютна і відносна розгалуженість.
Принципи побудови логарифмічних частотних характеристик.
6.3 Приклади розв'язання задач
Задача 1. Коло складається з котушки індуктивності (R, L), з'єднаної послідовно з конденсатором без втрат. Амплітуда прикладеного до всього кола напруги Um = 35 B. Частота вхідного гармонійного сигналу дорівнює резонансній частоті. Зобразити векторну діаграму, визначити добротність контуру і напругу на котушці, якщо амплітуда напруги на конденсаторі дорівнює 120 В.
Розв'язок.
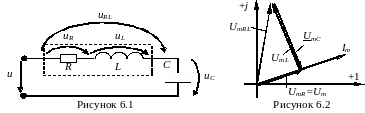
Зобразимо схему кола (рис. 6.1).
Відомо, що при резонансі вхідний опір
кола чисто активний і дорівнює R,
тому струм у колі збігається за фазою
з вхідною напругою; вхідна напруга
дорівнює напрузі на резисторі. Також
при резонансі амплітуди напруг на
реактивних елементах рівні між собою
й у Q
(добротність) раз більше, ніж прикладена
до кола напруга, тобто
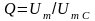 ;
по фазі напруги на реактивних елементах
зрушені на 1800.
Описані співвідношення між струмом і
напругами зображені на векторній
діаграмі рис. 6.2. Напруга
на котушці дорівнює сумі векторів напруг
на резисторі і на індуктивності:
UmRL=Um+Um.
Оскільки напруги Um
і Um
зрушені на 900
(рис. 6.2), то довжину вектора UmRL
(тобто амплітуду напруги на котушці)
можна знайти, вирішивши прямокутний
трикутник (довжина катетів Um
і Um
відома):
;
по фазі напруги на реактивних елементах
зрушені на 1800.
Описані співвідношення між струмом і
напругами зображені на векторній
діаграмі рис. 6.2. Напруга
на котушці дорівнює сумі векторів напруг
на резисторі і на індуктивності:
UmRL=Um+Um.
Оскільки напруги Um
і Um
зрушені на 900
(рис. 6.2), то довжину вектора UmRL
(тобто амплітуду напруги на котушці)
можна знайти, вирішивши прямокутний
трикутник (довжина катетів Um
і Um
відома):
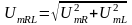 .
.
За умовою, амплітуда напруги на конденсаторі UmС = 120 B. Тоді Q = 120/35 3,428.
Як зазначалося вище,
UmR = Um = 35 В
і Um = UmС = 120 B,
тоді
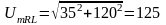 В.
В.
Відповідь: Q 3,428, UmRL = 125 В.
6.4 Варіанти задач
6.4.1 Послідовний коливальний контур улаштований на резонанс при кутовій частоті 5000 рад/с і споживає потужність 0,1 Вт при струмі 0,1 А. Напруга на конденсаторі 200 В. Знайти параметри кола R, L, C і прикладену до нього напругу.
6.4.2 Знайти параметри котушки (R, L), ємність С конденсатора й опір реостата R1, що включено в коло рис. 6.3, якщо при резонансі прилади показали: U = 200 B, U1 = 204 B, U2 = 180 B, I = 4 A. Частота перемінного струму f = 50 Гц. Побудувати векторну діаграму струмів і напруг.
6.4.3 Послідовний коливальний контур RLC підключений до джерела синусоїдальної ЕРС з Еm = 1,6 В і внутрішнім опором Ri = 16 Ом. При якому опорі R у контурі виділиться максимальна потужність при резонансі і чому вона дорівнюватиме? Знайти напруги на ємності, індуктивності і на опорі R при резонансі, якщо резонансна частота 100 кГц, а індуктивність L = 4,5 мГн. Побудувати векторну діаграму струмів і напруг.
6.4.4 Розрахувати елементи рівнобіжного коливального контуру (рис. 6.4) зі смугою пропускання 25 кГц, резонансною частотою 1 МГц і хвильовим опором контуру 75 Ом.
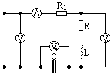
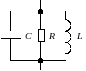
Рисунок 6.3 Рисунок 6.4
