3. Резервирование с восстановлением работоспособности отказавших элементов

Рассмотрим функционирование системы, состоящей из 2-х одинаковых элементов, работающих в режиме нагруженного ре­зервирования. После отказа одного из элементов немедленно на­чинается восстановление его работоспособности. Если отказав­ший элемент восстанавливается прежде, чем откажет 2-й элемент, то система возвращается в исходное состояние. Если в течение времени восстановления отказавшего элемента происходит отказ и второго элемента, то система полностью отказывает, прекра­щается ее функционирование, но при этом продолжается восста­новление работоспособности элемента, отказавшего первым. После его восстановления система вступает в работу, и одновре­менно начинается восстановление второго элемента, после его восстановления система возвращается в исходное состояние. Да­лее процесс функционирования происходит аналогично.

Допустим, что время безотказной работы обоих элементов и время восстановления их работоспособности являются случайны­ми величинами, распределенными по экспоненциальному закону.

Обозначим:

— вероятность безотказной работы одного элемента;

λ = 1 IT—интенсивность отказов;

Т—среднее время безотказной работы (средняя наработка до отказа);

— вероятность восстановления работоспособ­ности отказавшего элемента;

— интенсивность восстановления;

Т_в — среднее время восстановления;

λΔt — вероятность отказа одного элемента за бесконечно ма­лый промежуток времени Δt;

— вероятность безотказной работы элемента за время At;

μΔt — вероятность восстановления работоспособности одно­го элемента за время Δt;

— вероятность того, что за время Δt работоспособ­ность отказавшего элемента не будет восстановлена.

При сделанных допущениях об экспоненциальном характере распределений времени безотказной работы и времени восстанов­ления процесс функционирования рассматриваемой системы яв­ляется марковским .

В процессе функционирования рассматриваемая система мо­жет находиться в следующих состояниях.

1. Оба элемента работают.

2. Один элемент работает, второй отказал и восстанавливается.

3. Оба элемента отказали, один из них восстанавливается, сис­тема отказала.

Если система находится в 1-м состоянии, то за время At она пе­рейдет во 2-е состояние при отказе одного из элементов. Если ни один из элементов не отказал, то система остается в 1-м состоянии. Вероятность безотказной работы двух элементов равна

Пренебрегая членом высшего порядка малости λ²Δt², полу­чаем, что вероятность

Вероятность отказа одного из двух элементов, т.е.

Если система находится во 2-м состоянии, то:

• она перейдет в 1-е состояние, если за время At произойдет вос­становление отказавшего элемента и не откажет второй эле­мент

• она перейдет в 3-с состояние, если за время не будет вос­становлен отказавший элемент и откажет второй элемент

• она останется во 2-м состоянии, если не перейдет ни в 1-е, ни в 3-е состояние

Если система находится в 3-м состоянии, то она перейдет во 2-е, если за время At закончится восстановление работоспособ­ности элемента, отказавшего первым,

Если восстановление работоспособности отказавшего эле­мента за время Δt не закончится, то система останется в 3-м со­стоянии

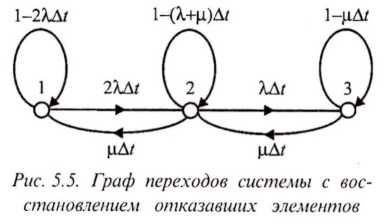
Граф переходов рассмат­риваемой системы изобра­жен на рис. 5.

Уравнения Колмогоро­ва, связывающие между со­бой вероятности состояний системы в моменты t и t+ Δt, записываются в виде:

Рисунок 5 – Граф переходов системы с восстановлением отказавших элементов

После соответствующих преобразований эта система конечно­разностных уравнений превращается в систему дифференциаль­ных уравнений

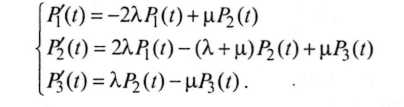
Граф переходов, показанный на рис. 5, является связным, поэтому процесс функционирования рассматриваемой системы имеет установившийся режим, в котором вероятности всех со­стояний перестают зависеть от времени, принимают финальные значения, а их производные равны нулю, при этом дифференци­альные уравнения превращаются в алгебраические

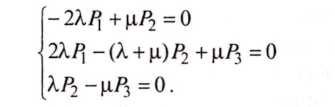
Полученную систему алгебраических уравнений решаем при условии

(12)

Из первого уравнения находим

Из третьего уравнения выражаем

Полученные выражения Р₂ и подставляем в 12:

Отсюда

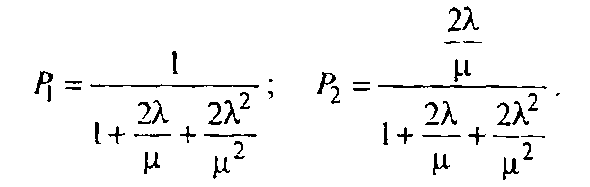
(13)

Рассматриваемая система находится в работоспособном состоянии и выполняет свои функции, пребывая в состояниях 1 или 2, поэтому коэффициент готовности этой системы К_г = Р₁ + Р₂, т.е.

Рассчитаем значение К_г при λ = 0,01 1/ч и u = 0,1 1/ч, т. е. каждый элемент отказывает в среднем один раз за 100 ч работы, и среднее время восстановления составляет 10 ч.

Расчет коэффициента готовности для нерезервированной системы дает значение

Расчет по формуле (13) дает значение. Таким образом, введение резервирования существенно повысило надежность системы, приблизив вероятность ее нахождения в работоспособном состоянии к 1, т.е. резервирование элементов с восстановлением работоспособности после отказа является эффективным способом повышения надежности технических объектов.