
- •Кафедра электротехники и электрических машин Лекция № 1 по дисциплине «Надежность электрооборудования предприятий и учреждений»
- •13.03.02 «Электроэнергетика и электротехника»
- •Безотказность электрооборудования
- •1. Основные понятия и термины надежности электрооборудования.
- •2. Показатели безотказности невосстанавливаемых объектов
- •3. Показатели безотказности восстанавливаемых объектов
3. Показатели безотказности восстанавливаемых объектов
Последовательность наступления отказов восстанавливаемого оборудования в процессе функционирования локомотива можно представить в виде следующей модели [6]. Наблюдение за новым (отремонтированным) оборудованием начинается в момент времени t = 0 . После функционирования в течение времени (наработки) τ1 возникает отказ, затем происходит восстановление или оборудование заменяют новым за время, несоизмеримо меньшее, чем наработка до отказа τ2. После наработки τ2 оборудование отказывает, и снова его ремонтируют или заменяют однотипным работоспособным. Далее процесс развивается аналогично. Поскольку все отказы возникают под действием одних и тех же факторов, естественно предположить, что наработки между отказами τ1 , τ2 ,..., τi,..., τn имеют один и тот же закон распределения F(t) = Р(τ <t).
Моменты отказов tl = τ1, t2= τ1 +τ2 , ..., tn = τ1 +τ2 +...+ τn образуют случайный поток, называемый процессом восстановления. Процесс восстановления оборудования локомотивов можно оценивать следующими показателями безотказности: вероятностью безотказной работы, средней наработкой на отказ и параметром потока отказов.
Определение параметра потока отказов осуществляется на основе функции восстановления H(t) — среднего числа отказов m(t) одного экземпляра оборудования за наработку t:
H(t) = M{m(t)},
гдеm(t)— число отказов одного объекта за наработку t.
Для опытного определения H(t) наблюдают за N экземплярами однотипного оборудования и фиксируют число отказов каждого из них в течение наработки t.
О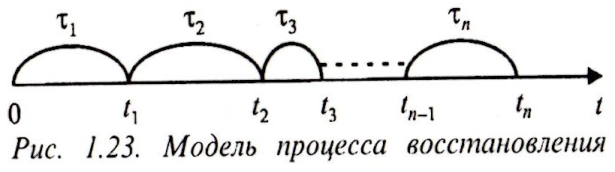 ценка
среднего числа
отказов, приходящихся
на один экземпляр рассматриваемого
оборудования, за наработкуtопределяется
следующим образом:
ценка
среднего числа
отказов, приходящихся
на один экземпляр рассматриваемого
оборудования, за наработкуtопределяется
следующим образом:
Модель
процесса восстановления
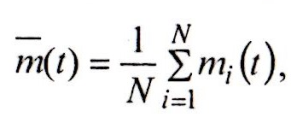
где mi (t) — число отказов i-го экземпляра оборудования за наработку t.
П![]()
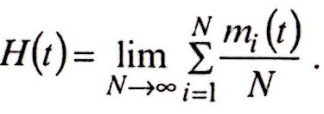 о
объединенному процессу восстановления,
полученному в результате наложения
N
процессов конкретных экземпляров
оборудования, можно графически
представить функцию среднего числа
отказов одного экземпляра оборудования
за время t
(рис.
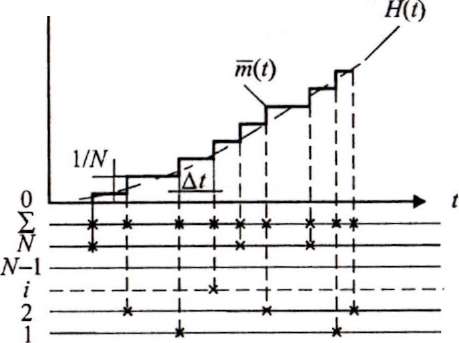
1.24). Зависимость m(t)
представляет
собой ступенчатую линию, величина
сохраняет
постоянное значение в промежутке между
отказами отдельных экземпляров
оборудования и возрастает скачком на
1/N
в момент
очередного отказа. Чем большее число
экземпляров однотипного оборудования
будет поставлено под наблюдение, тем
меньше будет интервал наработки Δt
между
соседними отказами и меньше окажется
скачок 1/N.
В
пределе при N→∞ —ступенчатая линия
стремится к некоторой непрерывной и
плавной кривой H(t), которая и является
ведущей функцией процесса восстановления,
т.е.
о
объединенному процессу восстановления,
полученному в результате наложения
N
процессов конкретных экземпляров
оборудования, можно графически
представить функцию среднего числа
отказов одного экземпляра оборудования
за время t
(рис.
1.24). Зависимость m(t)
представляет
собой ступенчатую линию, величина
сохраняет
постоянное значение в промежутке между
отказами отдельных экземпляров
оборудования и возрастает скачком на
1/N
в момент
очередного отказа. Чем большее число
экземпляров однотипного оборудования
будет поставлено под наблюдение, тем
меньше будет интервал наработки Δt
между
соседними отказами и меньше окажется
скачок 1/N.
В
пределе при N→∞ —ступенчатая линия
стремится к некоторой непрерывной и
плавной кривой H(t), которая и является
ведущей функцией процесса восстановления,
т.е.
П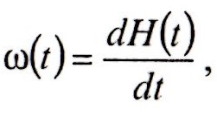 о
функции восстановления определяется
параметр потока отказов оборудования:
о
функции восстановления определяется
параметр потока отказов оборудования:
который характеризует скорость нарастания числа отказов при различных значениях наработки.
Параметр потока отказов оценивается по статистическим данным с помощью выражения:
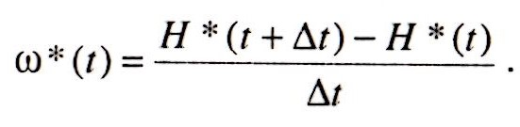
Статистические оценки функции восстановления в моменты t и t+ Δt определяются по формуле:
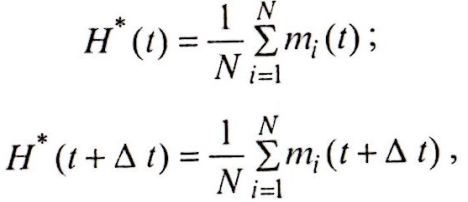
где mi(t)и mi(t+ Δt) — число отказов i-го объекта за наработку t и (t+ Δt) соответственно.
Подставив получим:
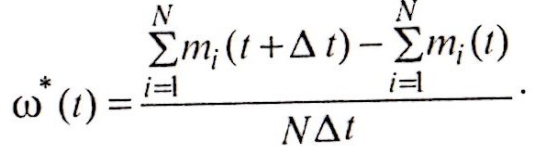
Поскольку числитель дроби представляет собой Δm — число отказов всех рассматриваемых объектов в интервале Δt, то окончательное выражение статистической оценки параметра потока отказов имеет вид:
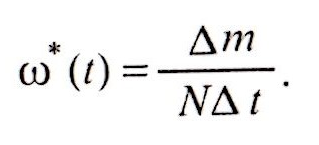
О![]() ценку
параметра потока отказов целесообразно
осуществлять на основе информации о
наработках между отказами оборудования
локомотивов, обусловленными какой-либо
конкретной причиной (например,
перебросы по коллектору, ползуны колесных
пар и т.п.). Для этого по наработкам между
отказами отдельных экземпляров
оборудования строят объединенный
процесс восстановления.
ценку
параметра потока отказов целесообразно
осуществлять на основе информации о
наработках между отказами оборудования
локомотивов, обусловленными какой-либо
конкретной причиной (например,
перебросы по коллектору, ползуны колесных
пар и т.п.). Для этого по наработкам между
отказами отдельных экземпляров
оборудования строят объединенный
процесс восстановления.
Функция
восстановления

Диаграмма
распределения оценки параметра потока
отказов по интервалам наработки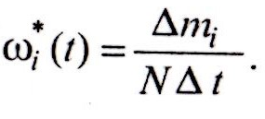 езультаты
наблюдений оформляют в виде таблицы ,
и они могут быть представлены в графической
форме ). Оценка параметров потока отказов
в i-ом
интервале наработки рассчитывается по
формуле :
езультаты
наблюдений оформляют в виде таблицы ,
и они могут быть представлены в графической
форме ). Оценка параметров потока отказов
в i-ом
интервале наработки рассчитывается по
формуле :
Таблица7
П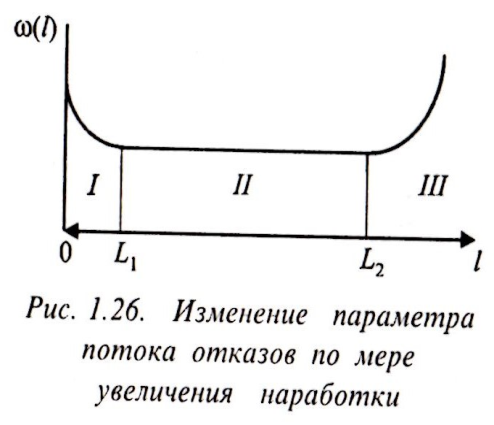 ри
N→∞ ширина интервала Δt→0 и ступенчатая
линия w*(t)
превращается в гладкую кривую w(t).
ри
N→∞ ширина интервала Δt→0 и ступенчатая
линия w*(t)
превращается в гладкую кривую w(t).
Измерение
параметра потока отказов по мере
увеличения наработки
Ilo зависимости w(t) можно рассчитать остальные показатели не безотказности восстанавливаемого оборудования — вероятность безотказной работы P(t) и среднюю наработку на отказ Т.
Взаимосвязь между показателями безотказности
11ри условии, что замена или восстановление отказавшего оборудования происходит мгновенно, процесс отказов можно представить в следующем виде. Допустим, что из N экземпляров однотипного оборудования, работоспособного в момент времени t, и интервале наработки Δt отказало Δm экземпляров .
Число экземпляров отказавшего оборудования Δm складывается из:
Δm1 — число экземпляров оборудования, ни разу не отказавшего в интервале [0, t],— так называемые первичные отказы;
Δm2 — число экземпляров оборудования, отказавшего в интервале [0, t], восстановленного и вновь отказавшего в интервале [t,t+Δt];
Δm= Δm1 + Δm2.
Общее число отказов в интервале [t,t+ Δt] по формуле находится так:
Δm = Nw(t)Δt
Вероятность
отказов оборудования
где w(t) — параметр потока отказов.
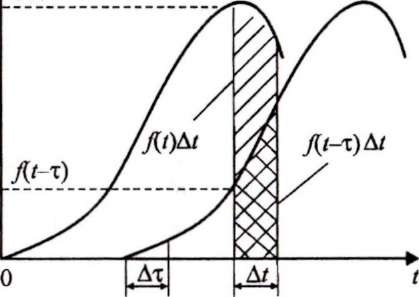
Так как Δm1 экземпляров оборудования ни разу не отказали в интервале от 0 до t ,то Δm1 можно определить через функцию плотности распределения наработки между отказами f(t) как для невосстанавливае-мого оборудования:
Δm1 = Nf(t)ΔtДля определения числа экземпляров отказавшего оборудования Δm2 выберем такой интервал Δτ, в течение которого вероятность отказа каждого из Δm2 экземпляров более одного раза является величиной бесконечно малой по сравнению с вероятностью одиночного отказа. Интервал [τ, τ + Δτ] лежит внутри промежутка [0, t]. В течение этого интервала отказало и заменено на новое (или полностью восстановлено) Nw(τ)Δτ экземпляров оборудования. Из их числа в интервале [t, t + Δt] вновь откажут, т.е. будут иметь повторный отказ ΔК экземпляров. Ведя отчет наработки элементов, отказавших в интервале Δτ, от момента τ, находим вероятность их повторного отказа в интервале Δt как f(t- τ)Δt; поэтому ΔК = Nw(τ)Δτf(t - τ)Δt.
С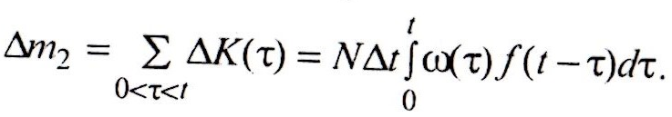 уммируя
ΔК по всем τ в интервале [0; t], получаем,
что из числа уже отказавших и восстановленных
до момента t
экземпляров
оборудования в интервале [t, t + Δt]
повторному отказу будет подвержено Δm2
экземпляров:
уммируя
ΔК по всем τ в интервале [0; t], получаем,
что из числа уже отказавших и восстановленных
до момента t
экземпляров
оборудования в интервале [t, t + Δt]
повторному отказу будет подвержено Δm2
экземпляров:
Подставив в выражение соответствующие выражения для Δm, Δm1, Δm2, получим:
 После
деления обеих частей выражения на NΔt
получаем
интегральное уравнение:
После
деления обеих частей выражения на NΔt
получаем
интегральное уравнение:
![]()
У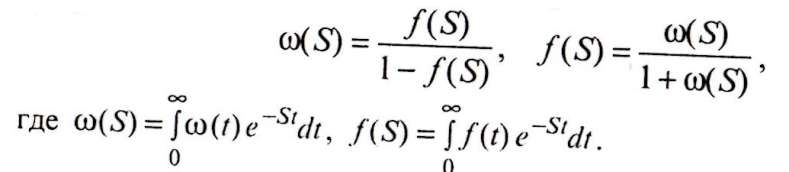 равнение
не всегда удается решить аналитически.
Если существуют преобразования Лапласа
w(S)
и f(S),то
в операторной форме параметр потока
отказов и функция плотности распределения
наработки между отказами выражается
следующим образом:
равнение
не всегда удается решить аналитически.
Если существуют преобразования Лапласа
w(S)
и f(S),то
в операторной форме параметр потока
отказов и функция плотности распределения
наработки между отказами выражается
следующим образом:
Аналитическое решение уравнения существует для нормального распределения наработки между отказами и распределения Эрнанга. Для других законов распределения решение уравнения не записывается в аналитических выражениях. Поэтому при решении практических задач, в основе которых лежит обработка первичной статистической информации, уравнение целесообразно ин-итрировать численными методами. При этом как до, так и после выполнения расчетов функции w(t) и f(t)оказываются заданными в виде дискретного ряда w(i) и f(i). Произведем замену t на L, а τ на l. Введем обозначение для подинтегральной функции :
F(L, l)= w(l)f(L- l).
В дискретной форме, после замены переменной L на п, а l на i выражение записывается в виде:
F(n, i) = w(i)f(n - i)
При n = 0 из уравнения получаем w0=f0.
Е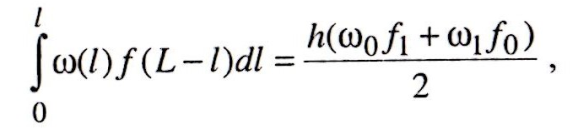 сли
n = 1, то, применив численный метод
интегрирования — метод трапеций ,
получим:
сли
n = 1, то, применив численный метод
интегрирования — метод трапеций ,
получим:
где h— шаг интегрирования.
Уравнение для этого случая записывается в виде:
![]()
(1.66)
При n= 2 имеем :
![]()
В этом случае уравнение принимает вид:
![]()
(1.67)
В общем случае для произвольного числа п имеем :
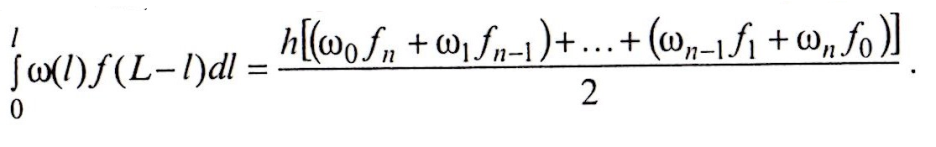
Из выражения (1.62) получаем:
(1.68)

Пояснения
к численному решению интегрального
уравнения при n=1;
n=2
общий случай
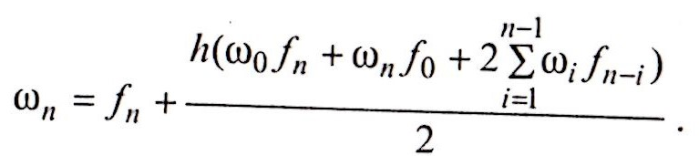
Таким образом имеем следующую систему уравнений:
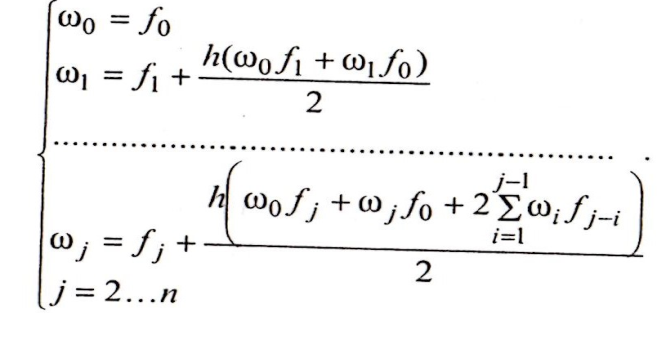
Cистема позволяет по известному дискретному ряду значений плотности распределения наработок на отказ fi найти ряд значений параметра потока отказов wi:

Если известен ряд значений параметра потока отказов со, то по системе уравнений можно осуществить обратное решение интегрального уравнения и определить ряд значений плотности распределения наработки на отказ:
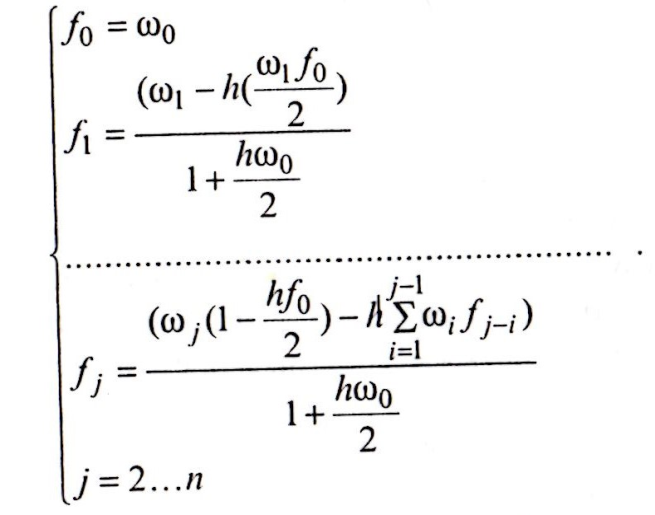
Применение метода конечных разностей при расчете параметра потока отказов является предпочтительным, особенно для случаев, когда вид закона распределения наработки между отказами априори неизвестен и определить его невозможно.
Блок-схема программы решения интегрального уравнения численным методом представлена на рисунке.
Для «прямого» решения уравнения по рекуррентным формулам переменной z задается значение, равное 1. При «обратном» решении по формулам z= 2.
Д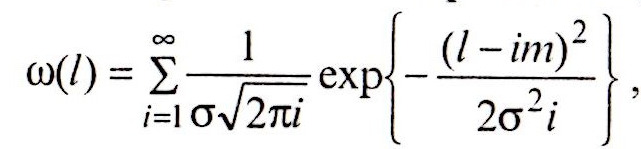 ля
нормального закона распределения
случайной величины существует
аналитическое решение интегрального
уравнения :
ля
нормального закона распределения
случайной величины существует
аналитическое решение интегрального
уравнения :
где m и σ — соответственно математическое ожидание и среднее квадратическое отклонение случайной величины (наработки между отказами);
l— значение наработки;
i— номер отказа от начала наблюдения.
В результате вычисления w(l) по выражению установлено, что при i > 10 значение w(l) практически не изменяется с увеличением l. На рисунке представлены результаты расчета параметра потока отказов типичного оборудования электровозов, реализованные численным методом решения уравнения , изложенным выше, и аналитически по формуле при i = 10. Вычисление значений параметра потока отказов численным методом осуществлялось с шагом h= Δl = 1 тыс. км. Выбор такого шага объясняется тем, что межремонтные пробеги локомотивов определены соответствующими документами с точностью до 1 тыс. км, а наработки на отказ оборудования тоже, как правило, округляются до 1 тыс. км. Поэтому выбранный шаг интегрирования позволяет получить максимально возможную степень приближения результатов к аналитическому решению.
Сопоставление результатов расчета параметра потока отказов , проведенное двумя методами, свидетельствует о практическом совпадении вплоть до второго отказа. Так как основной задачей является предотвращение первого отказа, до которого функции, полученные в результате численного и аналитического решения совпадают, то точность численного метода можно считать достаточной.
Обычно на практике по статистическим данным об отказах рассчитываются оценки параметра потока отказов в различных интервалах наработки Δl, а по ним, решая интегральное уравнение
Блок-схема
программы решения интегрального
уравнения
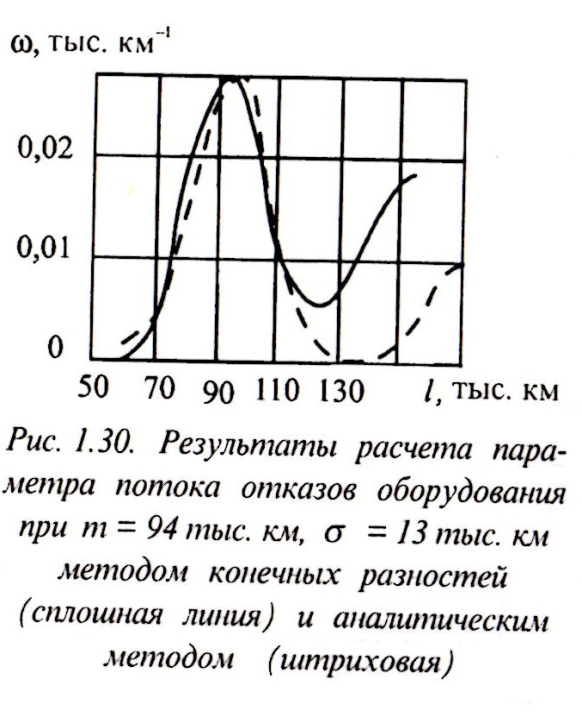
Результаты
расчёта потока отказов оборудования
при m=94тыс.км.
σ=13 тыс.км. методом конечных
разностей(сплошная линия) и аналитическим
(штриховая)
определяют плотность распределения наработки между отказами в виде дискретного ряда f0, f1, ...,fn„. Интегрируя функцию f(l) определяют вероятность отказов Q(l) и находят вероятность безотказной работы: P(l) =1 - Q(l) а затем, интегрируя функцию Р(l) в пределах от 0 до ∞ находят среднее значение наработки на отказ.
Изложенные алгоритмы расчета показателей безотказности восстанавливаемых объектов реализованы при решении следующих задач
