2. Показатели безотказности невосстанавливаемых объектов

При решении задач надежности сборочных единиц электрооборудования су­щественное значение имеет определение их как объектов восста­навливаемых или невосстанавливаемых, ремонтируемых или неремонтируемых, что всецело зависит от решения, принимаемо­го при отказе объекта.

Как и вообще для любых технических устройств, согласно ГОСТ 27.002-89 восстанавливаемым в некоторой конкретной си­туации является тот объект, работоспособность которого в дан­ных условиях может быть восстановлена.

Имеются сборочные единицы, которые теряют свойство восстанавливаемости при дости­жении некоторой наработки, когда их размеры или состояние выходят за допустимые пределы. Однако большинство сборочных единиц можно определить однозначно как восстанавливаемые или невосстанавливаемые по всему сроку службы до предельного состояния.

Н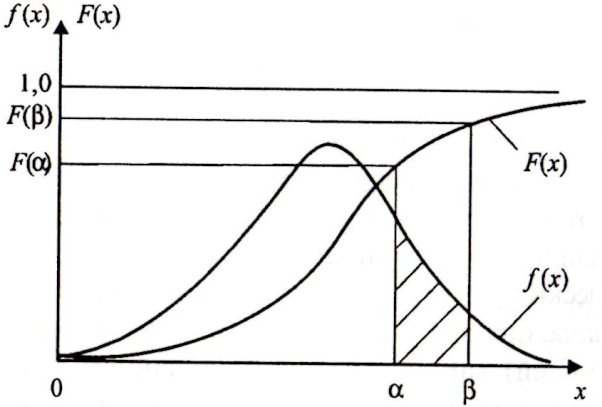 апример, элементы электроники, полупроводниковые вентили, подшипники качения, различные пружины (при потере упругости и появлении трещин) — суть невосстанавливаемые объекты в любой эксплуатационной ситуации. Для условий ремонтного завода многие основные узлы электрооборудования, такие как дизель, электрические машины и аппараты, редукторы, рамы, ударно-сцепные устройства и т.п., — восстанавливаемые объекты. Следовательно, при анали­зе, исследовании и разработке мер повышения надежности необхо­димо оценивать и определять ситуации, в которых возможно или невозможно восстановление работоспособности объекта.

Безотказность любого технического изделия (объекта) харак­теризуется наработкой до отказа — продолжительностью его бе­зотказной работы t, т.е. продолжительностью работы объекта от момента ввода в эксплуатацию до отказа.

Поскольку наработка до отказа зависит от множества случайных факторов — качества изготовления изделия, режимов его нагружения, порядка чередования различных эксплуатационных режимов, клима­тических и метеорологических условий эксплуатации, квалификации обслуживающего персонала, она является случайной величиной.

Полной (исчерпывающей) характеристикой случайной вели­чины является закон ее распределения, т.е. соотношение, которое устанавливает связь между возможными значениями случайной величины и соответствующими им вероятностями.

Наработка до отказа является непрерывной случайной величи­ной, для которой закон распределения задается либо в виде функ­ции распределения F(x), либо — плотности распределения f(х).

Плотность вероятностей f(x) и функция распределения F(x) непрерывной случайной величины

Функцией распределения случайной величины X называется функция F(x), выражающая вероятность того, что X примет зна­чения меньше, чем x:

F(x)=Р(Х<х).

Поскольку наработка до отказа — существенно положитель­ная величина, она определена на интервале [0,∞].

Функция распределения есть неубывающая функция, облада­ющая следующими свойствами:

F(0) = 0; F(∞) = 1;

F(x₁) ≤ F(x₂)при х₁ < x₂;

Р(а< X < Р) = F(β) - F(a).

Плотностью распределения непрерывной случайной величины называется первая производная от функции распределения:

Функцию распределения F(x)и плотность распределения f(х) называют законом распределения в ин­тегральной и дифференциальной форме соответственно. Графики этих функций показаны на рисунке.

Наиболее часто используемые в теории надежности рас­пределения случай­ных величин приве­дены в таблице.

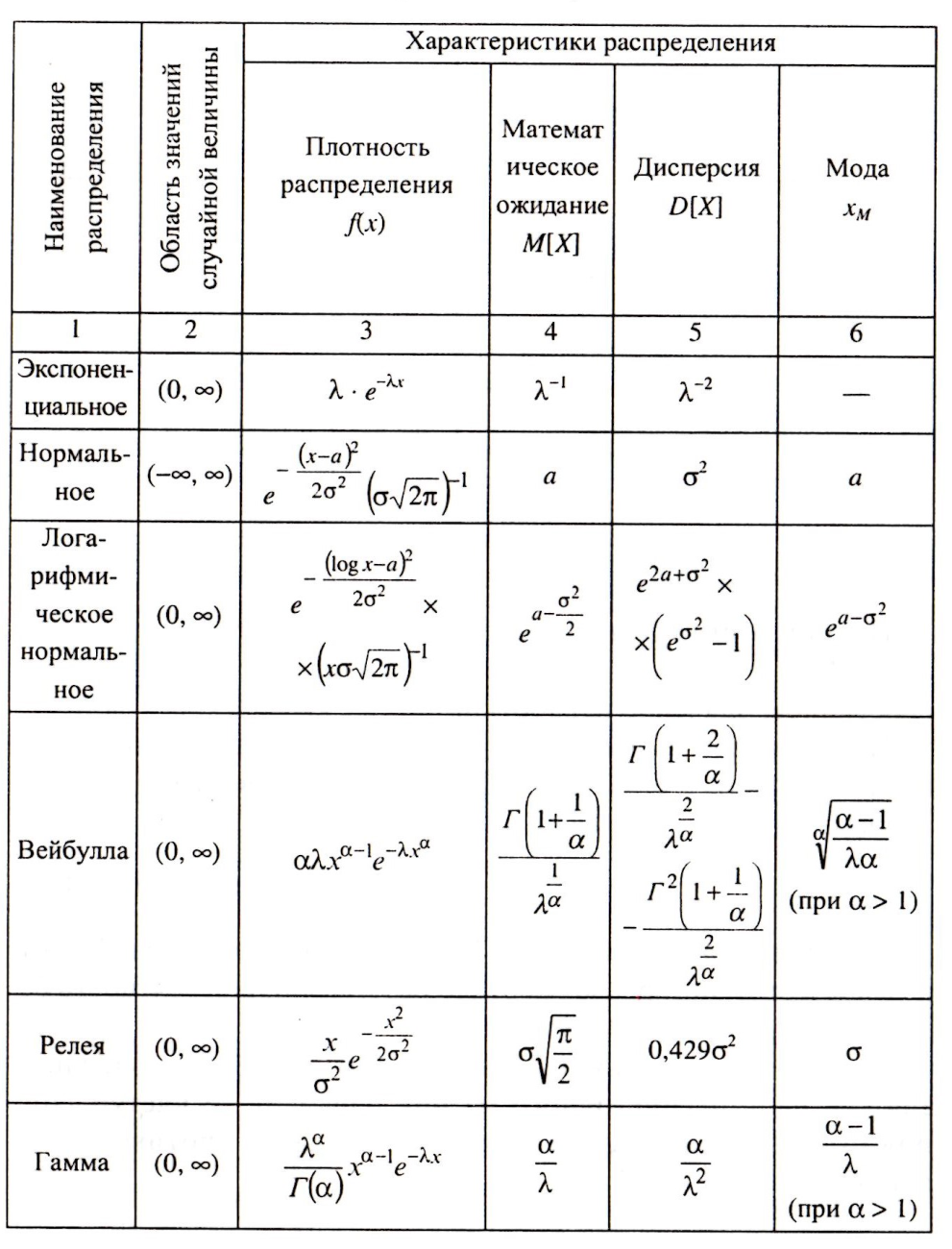Таблица 1

Непрерывные распределения случайных величин

Пусть известна функция распределения наработки до отказа F(t) = Р{τ < t}.Здесь т — наработка до отказа; t— заданное (фик­сированное) значение наработки.

Неравенство τ < t означает, что отказ произошел в интервале наработки [0,t], т. е. F(t)- вероятность отказа в интервале [0, t].

Обозначим ее Q(t). Таким образом

Q(t) = F(t)

Если в интервале наработки [0, t] отказ не произошел, значит, изделие в этом интервале работало безотказно, и вероятность бе­зотказной работы

Р(t) = Р{ τ > t}.

Отказ и безотказная работа — события противоположные, так как наступление одного из них означает не наступление другого. Известно, что сумма вероятностей противополож­ных событий равна 1.

P(t)+Q(t)=1.

По значению одной из величин P(t) или Q(t) можно рас­считать и другую:

Окончание таблицы 1

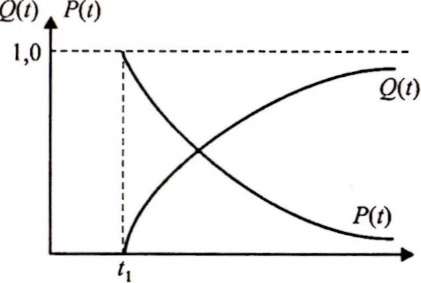
Графики функций Q(t) и P(t)показаны рисунке.

Зависимость вероятно­сти безотказной работы P(t) и вероятности отказов Q(l) от на­работки.

В аналитические выражения функций f{t), F{t), P(t )и Q(t) входят некоторые константы, которые называются числовы­ми характеристиками случай­ной величины, важнейшими из которых являются математи­ческое ожидание и дисперсия.

Средняя наработка до отка­за.

Средняя наработка до от­каза — математическое ожидание наработки объекта до первого отказ.

По определению математическое ожидание выражается как:

T= tf(t)dt,

где Т—средняя наработка до отказа.

Физически Т— центр, вокруг которого группируются значе­ния случайной величины наработки объекта до первого отказа.

Преобразуем выражение:

Проинтегрируем выражение по частям:

∫udv=uv-∫vdu.

Здесь

и = t, du= dt, dv= dP(t), v=P(t).

Применив эти выражения , получим:

П ри t→∞ произведение tp(t)→0, так как P(t )принимает нулевое значение при конечном значении t. При t→0 произ­ведение tp(t) также стремится к нулю, так как P(0) = 1. То есть про­изведение tP(t) равно нулю при подстановке как верхнего, так и нижнего пределов интегрирования. Окончательно:

T= P(t)dt.

Отсюда следует, что средняя наработка до отказа численно рав­на площади, ограниченной графиком функции P(t). Этим соотно­шением удобно пользоваться для вычисления средней наработки до отказа, особенно при расчетах, не требующих высокой точности.

Например, пусть известны графики P₁(t) и P₂(t) двух одно­именных объектов.

Без проведения расчетов можно сделать вывод, что второй элемент отказывает примерно в 2 раза реже, чем первый, так как площадь T₂ ≈ 2T₁.

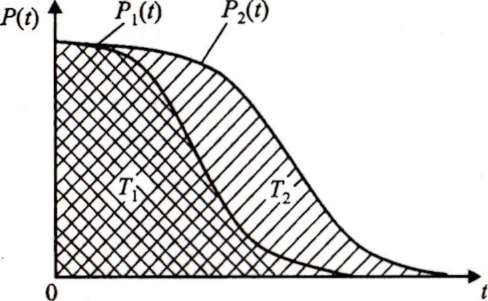
Графическая интерпрета­ция средней наработки до отказа

С редняя наработка до отказа показывает только центр, вокруг ко­торого группируются значения случайной величины. Степень раз­броса, отклонения случайной величины от центра характеризует дис­персия, которая является математическим ожиданием квадрата откло­нения случайной величины от ее математического ожидания:

D_t= (t-T)² f(t)dt.

При практическом использовании дисперсия неудобна в том от­ношении, что она имеет размерность квадрата случайной величи­ны. Например, если наработка до отказа имеет размерность млн км, то размерность дисперсии (млн км)², если наработка измеряется в часах, то размерность дис­персии ч² и т.д. Для устра­нения этого недостатка из дисперсии извлекается квад­ратный корень, и этот пока­затель называется средним квадратическим отклонени­ем (СКО) и обозначается как σ:

σ_t =√D_t .

Еще одним показателем разброса случайной величины явля­ется коэффициент вариации, который представляет собой отно­шение СКО к математическому ожиданию случайной величины:

V_t = σ_t / T .

Числовые характеристики (параметры) большинства применя­емых на практике распределений случайных величин могут быть выражены через математическое ожидание и дисперсию (или СКО) случайной величины.

Выражения устанавливают соотношение между вероятностными величинами. На практике по результатам на­блюдений или испытаний рассчитывают их статистические ана­логи — статистические оценки.

Статистическая оценка показателей безотказности. Пусть под на­блюдение поставлено N однотипных невосстанавливаемых в пути сле­дования объектов, например тяговых двигателей электровозов, или электрических аппаратов определенного типа и т.п. В процессе эксплуатации объектов фиксируются момен­ты возникновения отказов и определяются наработки до отказа τ₁, τ₂,... ..., τ_N. Здесь τ_i — наработка до отказа i-го объекта; i= 1, 2, ..., N.

Объекты пронумерованы в порядке их отказов. Числовая после­довательность τ₁, τ₂,... ..., τ_N - может быть представлена в виде ряда то­чек на оси наработки t .Число точек равно числу наблюда­емых объектов N, так как после отказа невосстанавливаемого объекта наблюдение за ним прекращается (выборка без возвращения).

Зафиксируем на оси наработки некоторое значение t. Введем обозначения:

m(t)— число объектов, отказавших в интервале [0, t]. В число m(t) входят только те объекты, для которых справедливо соотношение τ_i < t;

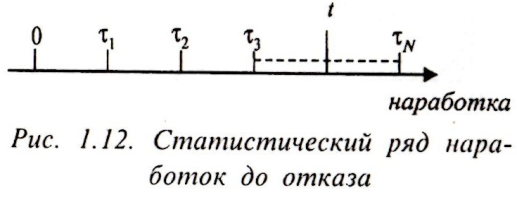
Статический ряд наработок до отказа

n(t) — число объектов, проработавших безотказно в интервале [0;t], для которых выполняется неравенство τ_i > t.

Отношение m(t) / N показывает долю объектов, отказавших в интервале [0,t], т.е. является статистической оценкой вероятнос­ти отказа рассматриваемых объектов:

Q^*(t)=

Аналогично статистическая оценка вероятности безотказной работы

P^*(t)=

Здесь символ * обозначает статистическую оценку.

Поскольку m(t) + n(t) = N, то Q*(t) + P*(t) = 1.

Можно утверждать, что Q*(t) является статистической оценкой функции распределения наработки до от­каза, т.е. Q*(t) = F*(t).

При изменении наработки t от 0 до τ_N, число отказов т(t) меня­ется от 0 до N, а значения статистической оценки функции распре­деления F*(t) увеличиваются от 0 до 1. График функции F*(t) пред­ставляет собой ступенчатую линию , которая скачкооб­разно увеличивается на 1/N в момент очередного отказа. В интер­вале наработки Δt между соседними отказами функция F*(t) сохра­няет постоянное значение.

При неограниченном увеличении числа наблюдаемых объектов N (объема выборки), т.е. при N →∞ интервал Δt→ 0 и величина скачка 1/N→ 0, таким образом ступенчатая линия F*(t) превраща­ется в непрерывную F(t).Иными словами, статисти­ческая функция распределения F*(t) сходится к своему вероятностному аналогу F(t) при N→∞, что являет­ся следствием действия закона больших чисел.

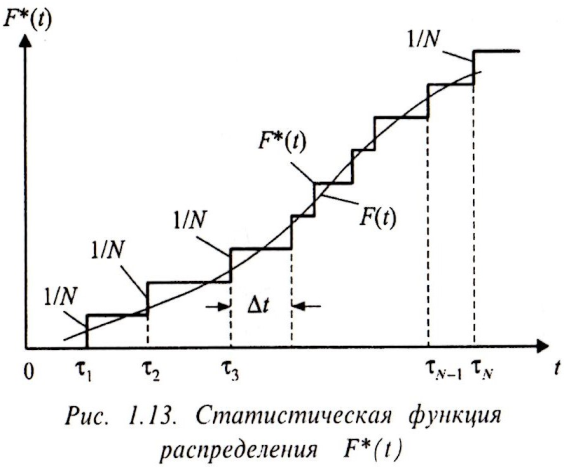
Статистическая функция распределения F*(t)

Статистической оценкой средней наработки до отказа являет­ся среднеарифметическое значение наработок до отказа всех на­блюдаемых объектов τ_i, i= 1, 2, ..., N:

Оценкой дисперсии наработки до отказа является среднеариф­метическое значение квадрата отклонения τ_i (i= 1, 2, ..., N) от оценки математического ожидания:

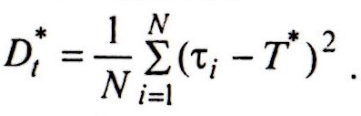При небольшом объеме выборки (N< 30) более точное зна­чение (несмещенная оценка) дисперсии получается при делении суммы квадратов отклонений на N - 1 :

В соответствии с законом больших чисел T* → T" и D*(t) → D(t) при N →∞ т. е. оценки математического ожидания и дисперсии случайной величины сходятся к своим вероятностным аналогам при неограниченном увеличении объема выборки.

Интенсивность отказов. Рассмотрим объект, проработавший безотказно в течение наработки t. Требуется определить вероят­ность того, что он проработает безотказно в течение еще некото­рой наработки Δt .

Обозначим Р [0; t] =P(t)— вероятность безотказной работы в интервале [0, t].

P[0;t+Δt] = P(t+ Δt)— вероятность безотказной работы в интер­вале [0, t + Δt].

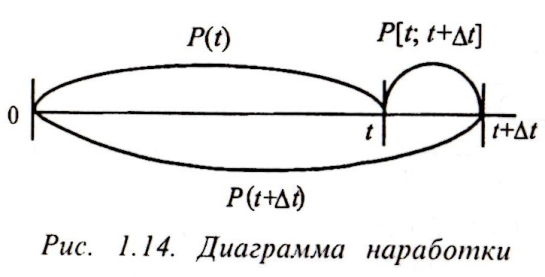
При достаточно малом интервале Δt

В ведем обозначение:

Тогда

Q[t, t+ Δt]= λ(t)Δt.

Величина λ(t) носит название интенсивность отказов, она по оп­ределению равна отношению производной от вероятности безотказ­ной работы к самой этой вероятности, взятому с обратным знаком.

Из выражения следует, что вероятность отказа в интер­вале [t, t+ Δt] при достаточно малой величине Δt пропорцио­нальна ширине интервала Δt, причем коэффициентом пропорци­ональности является интенсивность отказов λ(t).

Вероятность безотказной работы:

P[t, t+ Δt]= 1 - λ(t)Δt.

Следует еще раз подчеркнуть, что соотношения справедливы только для малых значений ширины интервала Δt.

С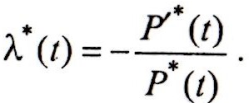 татистическая оценка интенсивности отказов. Следует:

где n(t) и n(t+ Δt) — число объектов, проработавших безотказно в тече­ние наработки t и t+ Δt соответственно; N — общее число наблюдаемых объектов (объем выборки).

Подставив, получим:

Подставив оценку производной P'*(t) и оценку вероят­ности безотказной работы P*(t) , получим оценку интенсивности отказов:

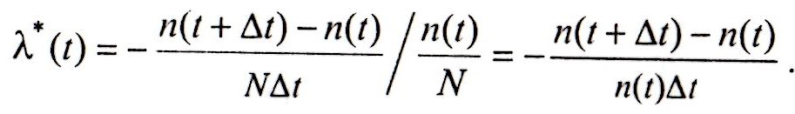
П оменяв местами слагаемые числителя, получим:

По физическому смыслу разность n(t)-n(t+ Δt)

п редставляет собой число отказов Δn в интервале [t, t+ Δt]. Отсюда:

Здесь ΔnΔAt — число отказов, приходящихся на единицу на­работки.

Таким образом, интенсивность отказов статистически пред­ставляет собой число отказов, приходящихся на единицу нара­ботки, отнесенное к числу объектов, сохранивших работоспособ­ность к началу рассматриваемого интервала наработки.

Поскольку Δn и n(t)— величины безразмерные, то следует, что размерность интенсивности отказов обратна размер­ности наработки. Например, если наработка измеряется в часах, то размерность интенсивности отказов будет 1/ч.

Построение эмпирической зависимости λ*(t)производится сле­дующим образом. Под наблюдение (на испытание) становится N одноименных объектов, которые эксплуатируются (испытываются) на протяжении наработки t. Весь интервал наработки разбивается на ряд интервалов группирования шириной Δt, и в каждом интервале фиксируется число отказавших объектов Δn. Отказавший объект изымается из эксплуатации (прекращаются его испытания). Таким образом, число наблюдаемых объектов постепенно умень­шается. Наблюдения (испытания) продолжаются до отказа после­днего объекта или в течение заранее заданной на­работки Т.

Результаты испытаний оформляются в виде таблицы (табл. 2).

Таблица 2

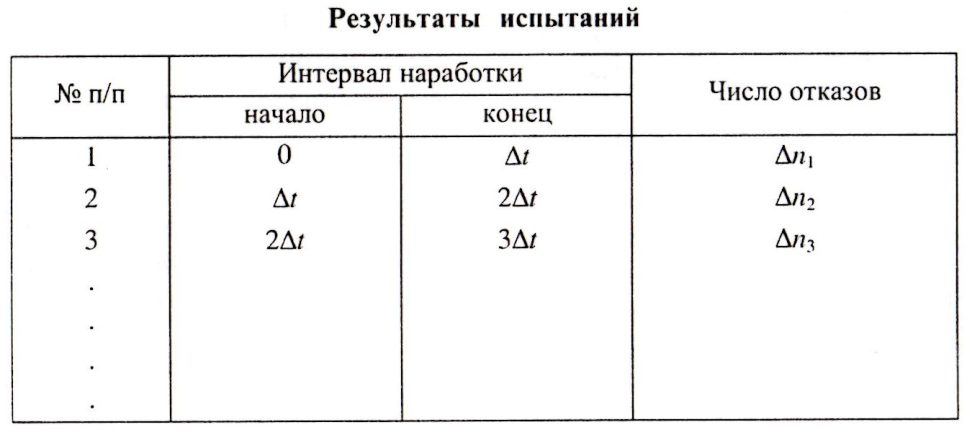
Здесь в первом интервале [0; Δt] отказали Δn₁ объектов, во вто­ром — [Δt ; 2 Δt]— Δn₂ и т. д.

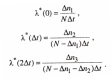
Рассчитывается статистическая оценка интенсивности отказов для каждого интервала:

Здесь в качестве аргумента функции λ*(t) выступает начало ин­тервала. Полученное значение интенсивности отказов считается постоянным в данном интервале Δt_i..

Результаты расчетов оформляются графически в виде диаграммы интенсивности отказов. Для построения диаграммы горизон­тальная ось наработки разбивается на интервалы шириной Δt, и на каждом из них строится прямоугольник, высота которого равна интенсивности отказов в данном интервале .

Здесь ступенчатая линия λ*(t) представляет собой эмпиричес­кую зависимость интенсивности отказов от наработки

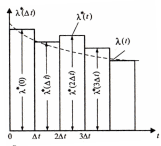
При неограниченном увеличении числа испытуе­мых объектов, т.е. при N °° ширина интервала группирования Д; —» 0 и ступенчатая линия превра­щается в гладкую кривую X(t),которая представляет собой теоретическую зави­симость интенсивности от­казов от наработки:

Диаграмма интенсивности отказов

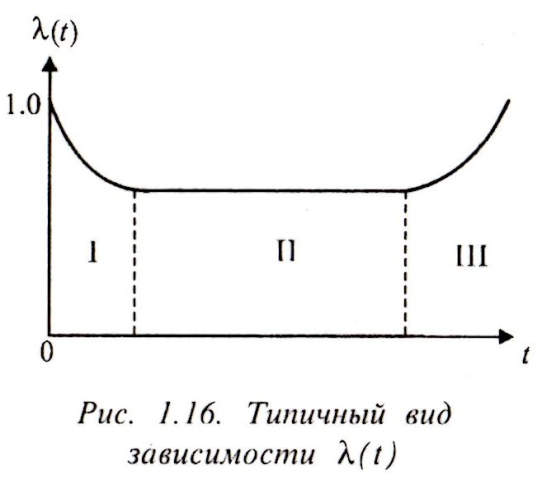
Типичный вид зависимости λ(t)

Для разных объектов и раз­личных условий эксплуатации могут быть получены совер­шенно различные зависимости λ(t), но типичный, т. е. наиболее часто встречающийся, вид кри­вой λ(t) показан на рис. 1.16.

Здесь четко различимы три разных периода наработки.

1. — период приработки, в течение которого отказывают в основном те объекты, которые имели скрытые дефекты изготовле­ния. Постепенно дефектные объекты выбраковываются, сопрягае­мые детали притираются (прирабатываются) друг к другу, число отказов уменьшается, и кривая λ(t)имеет убывающий вид.

2. — период нормальной эксплуатации, в котором λ(t) = const— интенсивность отказов является постоянной величиной. В этом пе­риоде причинами отказов являются:

• Конструкционные недостатки.

• Ошибки обслуживающего персонала.

• Неблагоприятные воздействия внешней среды. Поскольку частота проявления каждой из указанных причин распределена во времени приблизительно равномерно, интенсив­ность отказов в периоде нормальной эксплуатации является по­стоянной величиной.

III — период усиленного износа, в котором износ трущихся поверхностей достигает предельно допустимой величины, возникает люфт, биение сопряженных деталей, растет динамическое напряже­ние и возрастает число повреждений механического оборудования; вследствие старения изоляции возрастает число ее пробоев, т.е. чис­ло и интенсивность отказов возрастают при увеличении наработки.

С целью уменьшения общего числа отказов производят обкат­ку после их изготовления или ремонта — «отсекают» приработочный период. Производят своевременную замену или ре­монт изношенных деталей — «отсекают» период усиленного изно­са. Число отказов в периоде нормальной эксплуатации может быть уменьшено путем проведения конструкционной или технологичес­кой модернизации при изготовлении или ремонте оборудования, повышения квалификации обслуживающего персонала.

Взаимосвязь между показателями безотказности. Обычно по результатам испытаний неремонтируемых объектов рассчитыва­ют статистическую функцию интенсивности отказов λ*(t), а через нее находят вероятность безотказной работы P*(t)и оценку сред­ней наработки до отказа Т.

Перепишем выражение в виде:

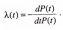
У множив обе части равенства на -dt, получим:

Проинтегрировав обе части равенства в пределах от 0 до t, по­лучим:

или с учетом того, что ln Р(0) = In1=0,

Потенцируя полученное выражение, имеем:

После вычисления функции P(t) по формуле находим среднюю наработку до отказа:

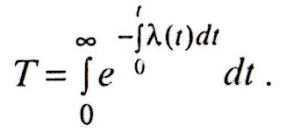
При практическом применении соотношений в них используются статистические оценки соответствующих пока­зателейx λ*(t), P*(t) и Т*.

Экспоненциальный закон надежности. Рассмотрим такие тех­нические объекты, у которых путем предэксплуатационной об­катки и своевременной замены изношенных деталей отсечены периоды приработки и усиленного износа. У таких объектов весь жизненный цикл от момента ввода в эксплуатацию до отказа или замены укладывается в период нормальной эксплуатации, т. е. интенсивность отказов λ = const. В этом случае соотношения между показателями безотказности существенно упрощаются.

Подставив постоянную λ, получим:

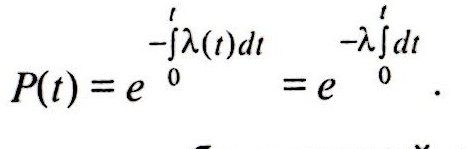
Окончательно вероятность безотказной работы определяется выражением:

Вероятность отказа:

Плотность распределения наработки до отказа:

Подставив в качестве P(t) выражение, получим среднюю наработку до отказа:

Подставив в качестве аргумента t верхний предел интегриро­вания, получим, что е^ ^-λt →0 при t →∞. Подстановка нижнего предела интегрирования дает значение е^ ^-λt , е^ ^-λ∙0=1

О кончательно имеем:

Подставив (1.42) и (1.43) в (1.22), вычислим дисперсию нара­ботки до отказа:

Дважды проинтегрируем по частям полу­ченное выражение. Введем обозначения:

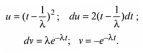
Отсюда

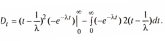
Первое слагаемое обращается в ноль при подстановке верх­него предела интегрирования, а при подстановке нижнего преде­ла оно равно 1/1², т.е.

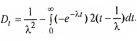
Возьмем входящий в данное выражение интеграл по частям, обо­значим:

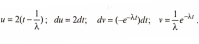
Следовательно:

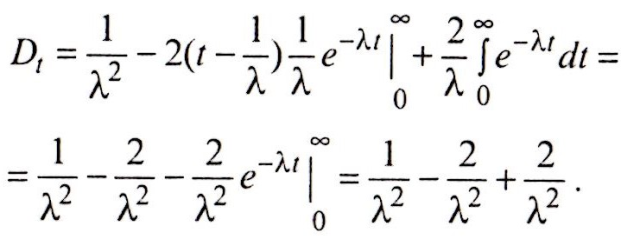
Окончательно имеем:

С реднее квадратическое отклонение σ_t = √D_t , будет определено как:

Графики функцийP(t), Q(t), f(t) приведены на рисунках.

З аметим, что среднее значение наработки до отказа, и среднее квадратическое отклонение, равны между собой, т. е.

Т= σ_t

Это равенство является характеристическим признаком экспо­ненциального закона распределения.

Простейший поток отказов. Рассмотрим группу из N одновре­менно работающих экземпляров однотипного оборудования, каждый из которых отказывает в случайный момент времени.

Зависимости вероятности отказа и вероятности безотказной работы от наработки

Последовательность собы­тий, заключающихся в отка­зах разных экземпляров дан­ного оборудования, принято называть потоком отказов, хотя фактически это единич­ные события. Если наработка до отказа каждого рассматри­ваемого объекта имеет экспо­ненциальное распределение, то поток отказов данного обо­рудования является простей­шим.

Зависимость плот­ности распределения от нара­ботки

Характерными свойствами про­стейшего потока являются: его ста­ционарность, означающая, что струк­тура потока не зависит от сдвига его по времени, иными словами, плот­ность потока постоянна; отсутствие последействия, заключающееся в том, что закон распределения числа отка­зов на любом промежутке времени не зависит от реализации потока до и после этого промежутка времени, т.е. взаимная независимость отказов; ординарность или невозможность одновременного возникновения двух и более отказов, иными слова­ми, отказы возникают поодиночке, а не группами.

Следствием этих свойств простейшего потока является то, что при суммировании большого числа простейших потоков образуется так­же простейший поток, если только среди них нет резко преобладаю­щего. Благодаря этому ряд показателей надежности сложных техни­ческих систем оказывается возможным определить как сумму ана­логичных показателей их деталей и узлов. Другое важное свойство простейшего потока отказов приводит к тому, что время работы между двумя соседними отказами как деталей и узлов, так и всего оборудования в целом, распределяется но экспоненциальному зако­ну, параметры которого легко рассчитать.

Экспоненциальный закон распределения ввиду своей просто­ты играет в теории надежности примерно такую же роль, что и закон Ома в электротехнике.

Подавляющее большинство электрических цепей нелинейны по своей физической природе. Это настолько усложняет их рас­чет, что делает его зачастую практически неосуществимым. Сто­ит только ввести допущения о линейном характере зависимости тока от напряжения для всех элементов электрической цепи (что и отражает закон Ома), как расчет этой цепи резко упрощается.

Аналогично в теории надежности. Очень часто законы распреде­ления наработки до отказа и других случайных величин, характеризующих надежность технических объектов, отличны от экспоненци­ального, что делает практически неосуществимым аналитический расчет надежности таких объектов. Введение допущения об экспоненциальности законов распределения позволяет получить выражения основных показателей надежности в аналитической форме. Следует, однако, помнить, что полученные таким образом результаты спра­ведливы лишь в первом приближении и нуждаются в дальнейшем уточнении с учетом реальных законов распределения.