
- •Контрольная работа
- •Москва 2020
- •1. СТАТИСТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ ПОКАЗАТЕЛЕЙ КАЧЕСТВА
- •Рис.1.1 График распределения результатов измерений при n=20
- •Рис.1.2. График распределения результатов измерений при n=10
- •Часть 1. Определение границ доверительного интервала
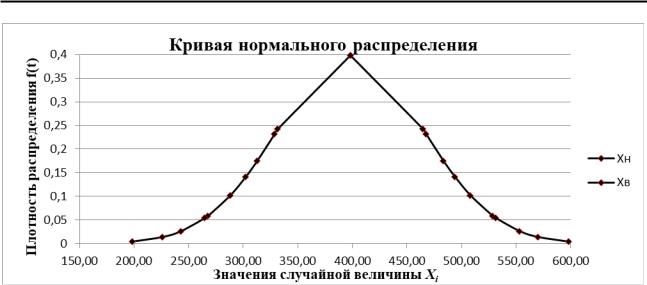
- •Рис.1.4. Кривая нормального распределения
- •Рис. 1.5. Доверительные интервалы
- •для выборок с
- •Анализ выборки из 20 измерений
- •Анализ выборки из 10 измерений
- •Вывод:
- •Анализ выборки из 5 измерений
- •Последовательность анализа выборки по критерию:
- •3. Построение теоретической кривой нормального распределения1.
- •Результаты вычисления критерия Пирсона
- •ПРИЛОЖЕНИЕ 1
- •ПРИЛОЖЕНИЕ 2
- •Значения коэффициента
- •ПРИЛОЖЕНИЕ 3
- •ПРИЛОЖЕНИЕ 4
0,997 |
3,0 |
198,06 |
597,84 |
0,04 |
|
|
|
|
|
По результатам вычислений строят кривую нормального распределения (рис. 1.4) и делают вывод о влиянии доверительной вероятности на ширину доверительного интервала.
Вывод: Чем выше значение доверительной вероятности, тем шире доверительный интервал _
Рис.1.4. Кривая нормального распределения
20

Часть 2. Определение границ доверительного интервала для истинного значения при Рдов 0,900.
Границы интервала для истинного значения Xист определяют по формуле:
Xист X tС X ,
|
|
|
|
|
|
||
где Х - среднее арифметическое значение результатов измерений; |
|||||||
|
tС - коэффициент Стьюдента, принимаемый по прилож. 2; |
||||||
|
|
|
- СКО среднего арифметического значения; |
||||
X |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
X |
|||
|
|
|
|
|
|
|
n |
где n - число измерений в выборке.
Таблица 1.6
|
|
|
|
|
|
|
|
|
|
|
Границы |
||
Число |
|
|
|
|
|
|
|
|
|
доверительного |
|||
|
|
|
|
|
|
|
интервала Xист |
||||||
измер. |
|
X |
|
|
tС |
tC |
|||||||
|
|
|
|
|
|
|
|
|
|
n |
|||
n |
|
|
|
|
|
n |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
левая |
|
правая |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Xист л |
|
Xист пр |
5 |
412,6 |
112,38 |
50,26 |
2,13 |
107,05 |
305,55 |
|
519,65 |
|||||
|
|
|
|
|
|
|
|
|
|||||
10 |
384,8 |
33,77 |
10,68 |
1,83 |
19,54 |
365,26 |
|
404,34 |
|||||
|
|
|
|
|
|
|
|
|
|||||
20 |
397,95 |
66,63 |
14,90 |
1,73 |
25,78 |
372,17 |
|
423,73 |
|||||
|
|
|
|
|
|
|
|
||||||
По результатам вычислений строят доверительные интервалы для |
|||||||||||||
единичного результата измерения X i |
и истинного значения |
X ист (рис. |
|||||||||||
1.5) при разном объеме статистических данных и делают вывод о влиянии количества измерений на ширину доверительного интервала.
Вывод: При увеличении объема статистических данных ширина доверительного интервала уменьшается.
21
22

Рис. 1.5. Доверительные интервалы |
X i и |
X ист |
для выборок с n 5, n 10, n 20 |
при |
Рдов 0,900 |
23

ПРАКТИЧЕСКАЯ РАБОТА № 4 Анализ статистического ряда измерений контролируемого
параметра и исключение результатов, содержащих грубые погрешности
Часть 1 Метод «трех сигм» (применяется для результатов измерений, распределенных по нормальному закону, и дает надежный
результат при числе измерений n 20)
Результат Xi содержит грубую погрешность, и его нужно исключить
из расчетов, если:
X |
сом |
|
|
|
|
|
|
3 |
|
|
сом |
|
||||||
X |
(если |
является минимальным значением) |
||||||||||||||||
|
|
|
|
|
|
|
X i |
|
||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
X |
сом |
|
|
|
|
|
|
|
|
|
|
сом |
|
|
||||
|
X |
|
(если |
|
является максимальным значением), |
|||||||||||||
|
|
|
|
|
3 |
|
X i |
|
||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где Х - среднее арифметическое значение результатов измерений без
учета сомнительных значений;
- СКО по выборке без учета сомнительных значений.
Сомнительным значением в выборке ( X |
сом |
) в первую очередь |
|
||
|
i |
|
является значение, имеющее наибольшее отклонение от X (см. табл. 1.1). Заполняется табл. 1.7 без учета сомнительного значения, т.к. оно исключается из выборки. Для выборки из 19 значений пересчитываются
значения среднего арифметического X и среднего квадратического отклонения .
Для выборки n 20 сомнительным значением является:
X n20 = 254
сомн
24
25

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Номер |
Результаты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X X |
|
( X X )2 |
|
|
|
|
|
|
Статистические |
||||||||||
измер |
измерения |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ения |
Xi |
i |
|
|
i |
|
|
|
|
|
|
характеристики |
||||||||
i |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
349 |
-56,53 |
|
|
|
3195,64 |
1. Среднее арифметическое значение |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
результатов измерений |
||||||||||
2 |
401 |
-4,53 |
|
|
|
20,52 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
3 |
436 |
30,47 |
|
|
|
928,42 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Xi |
|
|
|
|
|
4 |
398 |
-7,53 |
|
|
|
56,70 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
X |
|
i 1 |
= 405,53 |
|
|||||
5 |
348 |
-57,53 |
|
|
|
3309,70 |
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
19 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6 |
403 |
-2,53 |
|
|
|
6,40 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2. Среднеквадратичное отклонение |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
7 |
494 |
88,47 |
|
|
|
7826,94 |
||||||||||||||
|
|
|
(СКО) |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
9 |
342 |
-63,53 |
|
|
|
4036,06 |
|
n |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
531 |
125,47 |
|
|
|
15742,72 |
|
|
|
|
|
|
( Х Х ) |
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
||||
11 |
355 |
-50,53 |
|
|
|
2553,28 |
|
|
i 1 |
|||||||||||
|
|
|
|
|
|
|
= 58,94 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
12 |
444 |
38,47 |
|
|
|
1479,94 |
|
|
|
|
|
|
|
18 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
356 |
-49,53 |
|
|
|
2453,22 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
445 |
39,47 |
|
|
|
1557,88 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
408 |
2,47 |
|
|
|
6,10 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
476 |
70,47 |
|
|
|
4966,02 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
449 |
43,47 |
|
|
|
1889,64 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
297 |
-108,53 |
|
|
|
11778,76 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
387 |
-18,53 |
|
|
|
343,36 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
386 |
-19,53 |
|
|
|
381,42 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Xi = 7705 |
( Xi X ) |
= 62532,72 |
|
|
|
|
|
|
|
|
|
|
||||||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак,
сом |
|
|
|
|
3 |
|
254<405,53-3*58,94 |
||||
X i |
|
|
X |
|
|
|
|
||||
|
|
|
|
254<228,71 |
|
||||||
|
|
|
|
|
или |
|
|||||
|
Xсомi |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
X |
3 |
|||
|
|
|
|
|
|
||||||
Вывод: Результат |
измерения X n |
20 |
|
|
=254 не содержит грубую |
||||||
|
|
|
|
|
|||||||
сомн
погрешность и его можно не исключать из расчетов.
26
