
Лекции / Лекция 7
.docxТема 5
МАГНИТНЫЕ ЦЕПИ
И ЭЛЕКТРОМАГНИТНЫЕ УСТРОЙСТВА
В теме 5 рассмотрены основные магнитные величины, кривые намагничивания магнитно-мягких материалов, основные законы магнитных цепей, расчет неразветвленных магнитных цепей с воздушным зазором (прямая и обратная задачи), магнитные потери в стали. Демонстрация электрических аппаратов и реле.
Установочная лекция 7 (2 ч)
Дидактические единицы:
5.1. Основные магнитные величины.
5.2. Кривые намагничивания материалов
5.3. Основные законы магнитных цепей.
5.4. Расчет неразветвленных магнитных цепей.
СОДЕРЖАНИЕ
5.1. Основные магнитные величины
Из курса физики известно, что электрическое и магнитное поля тесно связаны между собой. В природе существует единое электромагнитное поле, а чисто электрическое и чисто магнитное поля являются лишь его частными случаями. Магнитное поле во всех без исключения случаях создаётся движущимися зарядами (в т.ч. вращающимися вокруг атомов и смещающимися в диэлектрике) или токами. Переменное магнитное поле обладает свойством создавать (индуктировать) электрическое поле.
Но электрическое поле оказывает магнитному полю такую же услугу. Переменное электрическое поле создаёт магнитное поле.
Таким образом, изменяющиеся электрическое и магнитное поля индуктируют друг друга. Взаимное индуктирование электрического и магнитного полей было открыто двумя великими учёными XIX в. Фарадеем и Максвеллом.
Напомним, что магнитное поле – вид материи, характеризующийся воздействием на движущиеся электрически заряженные частицы с силой, пропорциональной заряду этой частицы и её скорости. Магнитное поле в пустоте, воздухе и в других немагнитных средах определяется во всех точках векторами магнитной индукция B и напряжённости магнитного поля H, а в ферромагнитных материалах – векторами индукции B , напряженности H и намагниченности M.
Магнитная индукция B – векторная величина, определяющая силу, действующую на движущуюся заряженную частицу со стороны магнитного поля в данной его точке. Магнитная индукция численно равна отношению силы Fc, действующей на заряженную частицу, к произведению заряда q и составляющей скорости v частицы, перпендикулярной к вектору силы, т.е. B = Fc/qv. Единица магнитной индукции [B] = Tл (тесла), т.е. магнитная индукция 1 Тл равна силе, действующей на 1 м длины проводника с током в 1 А.
Магнитным потоком Ф через какой-либо контур в однородном поле называют произведение магнитной индукции В на площадь Sм этого контура и на косинус угла α между направлением индукции и нормалью к поверхности контура:
Ф = ВSмcosα.
Единица магнитного потока: [Ф] = [B]·[S] = Tл·м2 = Вб (вебер).
Если принять, что вектор магнитной индукции B одинаков во всех точках поверхности Sм и направлен перпендикулярно этому сечению, то его поток можно записать как Ф = ВSм.
В ряде случаев, например, при протекании тока в катушке, магнитный поток несколько раз сцепляется с витками катушки. В первом приближении можно считать, что все линии магнитной индукции сцепляются со всеми витками w катушки.
Тогда потокосцепление катушки связано с потоком Ф в одном витке простым соотношением:
Ψ = wФ [Вб].
Напряжённость магнитного поля H [А/м] – векторная величина, равная геометрической разности магнитной индукции B, делённой на магнитную постоянную µ0, и намагниченности M вещества, т.е.
H = B/µ0 M.
Векторы B и H необязательно совпадают друг с другом по направлению. Несовпадение может быть в анизотропных (в магнитном отношении) материалах, у которых величина µ зависит от направления вектора H. Большинство практических расчётов производят в предположении совпадения векторов B и H.
Зависимость B от H принято записывать в виде
B = µаH = µµ0H,
где µ0 = 4π·10-7 Гн/м (генри на метр) – магнитная постоянная, магнитная проницаемость пустоты; µa = µ0µ [Гн/м] – абсолютная магнитная проницаемость среды (вещества); µ = µa/µ0 – безразмерная относительная магнитная проницаемость вещества, показывающая, во сколько раз магнитная проницаемость среды (вещества) больше (меньше) магнитной проницаемости пустоты.
В зависимости от значения µ различают: диамагнетики с магнитной проницаемостью µ < 1 (например, серебро, медь висмут; они незначительно ослабляют магнитное поле), парамагнетики с µ > 1 (например, платина, алюминий, воздух; магнитное поле в них незначительно возрастает) и ферромагнетики с магнитной проницаемостью µ >> 1.
3.2. Кривые намагничивания ферромагнетиков
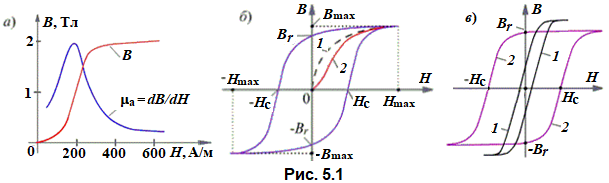 Зависимость
магнитной индукции В
от
напряжённости Н
магнитного поля, т.е. В
= ƒ(Н),
нелинейная (рис. 5.1а)
и не имеет аналитического выражения.
Для оценки свойств ферромагнетиков
строят кривые
намагничивания В =
ƒ(Н),
приводимые в справочниках. С их помощью
можно для каждого значения напряжённости
поля Н
определить значение магнитной
проницаемости µa,
которая при возрастании напряжённости
поля сначала увеличивается, затем
уменьшается, стремясь к магнитной
проницаемости µ0.
Зависимость
магнитной индукции В
от
напряжённости Н
магнитного поля, т.е. В
= ƒ(Н),
нелинейная (рис. 5.1а)
и не имеет аналитического выражения.
Для оценки свойств ферромагнетиков
строят кривые
намагничивания В =
ƒ(Н),
приводимые в справочниках. С их помощью
можно для каждого значения напряжённости
поля Н
определить значение магнитной
проницаемости µa,
которая при возрастании напряжённости
поля сначала увеличивается, затем
уменьшается, стремясь к магнитной
проницаемости µ0.
При протекании переменного тока в катушке с ферромагнитным сердечником происходит (в течение каждого периода тока) перемагничивание сердечника, которое на графике выглядит в виде петли – петли гистерезиса (рис. 5.1б). Если первоначально ненамагниченный ферромагнетик намагнитить до насыщения (кривая 1), а затем уменьшить и потом снова увеличивать напряженность магнитного поля Н (ток в катушке), то изменение индукции В не будет следовать начальной кривой: каждому значению напряжённости соответствуют два значения магнитной индукции в зависимости от того, увеличивается или уменьшается напряженность поля.
Величину магнитной индукции ±Br (см. рис. 5.1б и в) сохраняющуюся при Н = 0, называют остаточной индукцией; напряжённость магнитного поля ±Hc, при которой индукция обращается в нуль, называют коэрцитивной силой. На рис. 5.1б обозначено: ±Hmax и ±Bmax – максимальные напряжённость и индукция магнитного поля в ферромагнетике; 2 – основная кривая намагничивания ферромагнетика, проведенная через вершины семейства гистерезисных кривых, каждая из которых соответствует определённому значению Hmax. Приводимые в справочниках зависимости В(H) – основные кривые 2 намагничивания, незначительно отличаются от кривых 1 первоначального намагничивания (см. рис. 5.1а). Важнейшей характеристикой ферромагнитных материалов является зависимость магнитной индукции В от напряжённости магнитного поля Н, т.е. В = ƒ(Н). В зависимости от величины коэрцитивной силы Hc и формы петли гистерезиса ферромагнетики подразделяют на три класса: магнитно-мягкие, магнитно-твердые и специальные. Магнитно-мягкие материалы с узкой круто поднимающейся петлёй гистерезиса с Hc < 200 А/м (рис. 5.1в, кривая 1). Их используют в трансформаторах, асинхронных двигателях и других устройствах переменного тока, т.е. там, где требуется иметь малые потери при перемагничивании – в магнитопроводах с большими переменными индукциями. К магнитно-мягким материалам относится электротехническая сталь (сплавы на основе железа с присадкой кремния от 4 до 4,8% и других элементов с наибольшей магнитной индукцией 1,5-1,9 Тл), технически чистое железо, литая сталь, и др. Магнитно-твердые материалы с коэрцитивной силой Hc > 4000 А/м (рис. 5.1в, кривая 2). Их применяют для изготовления постоянных магнитов, которые должны иметь большие значения Hc. К ним относятся литые сплавы на основе Fe-Co-Ni-Al типа ЮНДК, бариевые сплавы (марки БИ), металлокерамические сплавы (ММК), сплавы кобальта с самарием, гадолинием и др. Постоянные магниты выполняют из литого чугуна, литой стали или из толстых штампованных листов стали с почти прямоугольной петлёй гистерезиса: с высокой остаточной индукцией Вr и большой коэрцитивной силой Hc (рис. 5.1в). Они характеризуются левой ветвью: от Br = 1,35…0,6 Тл до −Нс (|Нс| = 40…200 кА/м), для которых энергия размагничивания на единицу объема Wр = Br|Нс| /2 = BrBr/2µ0 = µ0Нс2/2 = 7…80 кДж/м3, а сила (в ньютонах [H]) притяжения электромагнитом листа стали при небольших двух зазорах между листом и его полюсами Fc = dWр/d = (Br)2Sм/ µ0 8105(Br)2Sм, где Fc – в ньютонах [Н]; Br = const в теслах [Тл]; Sм – в квадратных метрах. Трудность расчёта реальных электромагнитов заключается в трудности вычисления эквивалентного магнитного сопротивления Rмэ магнитной цепи с учётом неоднородности поля и в трудности учёта потока рассеяния, выходящего через боковые поверхности магнита. Специальные магнитные материалы, характеризуемые либо особой формой петли гистерезиса, например, прямоугольной (ферриты марки Вт и др.), либо специфическими свойствами: с сильной зависимостью магнитных свойств от температуры (сплавы никеля с медью марки Н38Х14 и др.); со значительными изменениями геометрических размеров при перемагничивании (магнитострикционные материалы из сплава железа с 14% алюминия и никеля или из сплава железа и кобальта марок НП-2-Т, 50КФ, 14НЮ); железокобальтовые сплавы – пермендюр с максимальной индукцией насыщения до 2,4 Тл; пермаллои (сплавы железа с никелем и добавками других металлов марок 79НМ, 80НХС и др.), имеющие большую магнитную проницаемость в слабых магнитных полях, и др. Площадь гистерезисной петли определяет расходуемую энергию в единице объёма ферромагнетика (нагревание магнитопровода) на преодоление упругих сил для принудительного поворота векторов намагниченности доменов в течение одного цикла перемагничивания. Потери энергии в магнитопроводе складываются как из потерь из-за гистерезиса – явления отставания изменения В от изменения Н, так и от протекания вихревых индуктированных в магнитопроводе токов. Вихревыми токами называют электрические токи проводимости, возникающие и замыкающиеся внутри электропроводного магнитопровода, находящегося в переменном магнитном поле. Потери, связанные с вихревыми токами, будут тем меньше, чем больше удельное сопротивление ферромагнитного материала и меньше толщина листов магнитопровода. Из этих листов штампуют пластины требуемой конфигурации; из изолированных друг от друга пластин составляют магнитопровод. 5.3. Основные законы магнитных цепей Типы магнитных цепей. Магнитная цепь – это совокупность устройств, содержащих ферромагнитные тела, электромагнитные процессы в которых могут быть описаны с помощью понятий магнитодвижущей силы, магнитного потока и разности магнитных потенциалов. Различают: • магнитные цепи с постоянными магнитами;
• Обычно в электромагнитных устройствах стремятся на пути магнитного потока разместить ферромагнитные материалы 2 с относительной магнитной проницаемостью µ = 500…10000, чтобы уменьшить величину тока намагничивающей обмотки 1 (рис. 5.2а). Однако между частями магнитопровода неизбежны воздушные зазоры (рис. 5.2б), или магнитопровод специально изготавливают с регулируемым зазором 3 (см. рис. 5.2а) с магнитной проницаемостью µ0. В низкочастотных устройствах (f < 1000 Гц) катушки размещают на ферромагнитных сердечниках, что приводит к многократному усилению магнитных потоков и их концентрации в самом ферромагнитном материале, и, как следствие, создается нужная конфигурация магнитного поля и магнитной цепи. Например, в четырёх полюсном генераторе постоянного тока (рис. 5.2б), катушки 4 возбуждения магнитного потока Ф размещены на полюсах статора; магнитные силовые линии проходят через соседние северный N и южный S полюсы, замыкаясь через статор 3 и цилиндрический якорь 1, при вращении которого в расположенной на нём обмотке индуктируется ЭДС. С помощью коллектора и щёток 2 обмотка якоря подключается к приёмнику энергии. Если вся магнитная цепь выполнена из одного ферромагнитного материала и имеет одинаковое сечение, то она называется однородной. Магнитная цепь, содержащая материалы с различными магнитными свойствами или имеющая воздушные зазоры, называется неоднородной. Магнитная цепь, во всех сечениях которой магнитный поток Ф одинаков, называется неразветвлённой. В разветвлённой магнитной цепи потоки на различных участках неодинаковы. Законы магнитных цепей. В ХIX в. рядом учёных установлена теснейшая связь между магнитными и электрическими явлениями, открыты индукционное и электродинамическое воздействия магнитного поля, лежащие в основе функционирования большинства современных электротехнических устройств. В частности, в 1820 г. Ампер произвёл опыты, в которых обнаружил механическое воздействие (электродинамическое действие) магнитного поля на проводник с током и между проводниками с токами. В 1831 г. Фарадей сообщил об открытии явления электромагнитной индукции. Он обнаружил индукционное действие магнитного поля - возникновение электрического тока в контуре, движущемся относительно магнита или относительно другого контура с током. В 1833 г. Ленц установил правило определения индуктированного тока, выражающее фундаментальный принцип электродинамики – принцип электромагнитной инерции. В 1873 г. Максвелл изложил в математической форме и расширил основные физические идеи Ампера, Фарадея и Ленца: Закон Ампера устанавливает связь между механической силой (направление которой определяют по известному правилу левой руки), магнитной индукцией, током и длиной проводника: сила, действующая на проводник с током в магнитном поле, равна произведению магнитной индукции, тока и длины отрезка проводника, перпендикулярного магнитной индукции, т.е.
где Fс – механическая сила, Н (ньютон); B – перпендикулярная проводнику (и току) составляющая магнитной индукции, Тл; l – длина проводника, м; I - ток, А. Закон Ампера лежит в основе функционирования электрических двигателей, реле и других электромагнитных устройств.
З где Ψ = Li – потокосцепление индуктивной катушки, Вб; w – число её витков; L = Ψ / i – индуктивность катушки, Гн, которая может быть приближённо определена через геометрические размеры катушки: L ≈ µµ0w2Sмlм, где lм – средняя длина магнитной силовой линии (м. с. л.); Sм – среднее сечение витков катушки, м2.
Д Закон электромагнитной индукции лежит в основе функционирования трансформаторов, генераторов электрического тока и других электромагнитных устройств. Закон полного тока устанавливает связь между магнитодвижущей силой F обмоток контура и напряжённостью магнитного поля H вдоль этого контура: линейный интеграл вектора напряжённости магнитного поля вдоль замкнутого контура равен полному току, заключённому в этом контуре:
З где Uм(а-b) – магнитное напряжение в амперах [А] между точками а и b. Для линейного участка a-b в однородном магнитном поле (H = const) магнитное напряжение Uм(а-b) = Hlа-b. Для практических расчётов интегралы заменяют суммой произведений Hklk, где индекс k указывает участок lk, вдоль которого Н и µ принимаются неизменными. В результате формула записывается в другом виде:
где n – число участков неразветвленной магнитной цепи
З где Hср = Вср/µa и Вср = Ф/S1 – средние напряжённость и индукция магнитного поля в сердечнике.
О или Ф = F/Rм, названное законом Ома для однородной магнитной цепи (по аналогии с законом Ома для электрической цепи: I = E / R),
г – магнитное сопротивление цепи, 1/Гн.
Отметим, что магнитное сопротивление Rм является функцией магнитной проницаемости µa = µ0µ среды (материала). Неизвестная величина µ в свою очередь зависит от величины магнитной индукции B (или магнитного потока Ф), что не позволяет непосредственно рассчитать магнитный поток. Если известны графики B(H) и µa(H) то, выбрав усредненное значение µa, можно найти приближенное значение потока Ф. Первый закон Кирхгофа. В разветвленных магнитных цепях имеется несколько замкнутых контуров и соответственно магнитных потоков. Для составления системы уравнений по законам Кирхгофа нужно знать направления токов в катушках, а также выбрать условные положительные направления магнитных потоков.
З т.е. алгебраическая сумма магнитных потоков в узле разветвления равна нулю. Под условным узлом разветвления магнитной цепи подразумевается точка, в которой сходятся три или большее число средних линий магнитной индукции. Второй закон Кирхгофа для неоднородной магнитной цепи. Для неоднородной магнитной цепи (рис. 5.6а) с несколькими обмотками и с участками с различными магнитными свойствами и площадями сечений магнитных потоков, закон полного тока имеет вид
H После несложных преобразований получим уравнение, называемое вторым законом Кирхгофа для магнитной цепи: U1м + U2м + Uδм = F1 – F2, где Ukм – магнитные напряжения в амперах [А] на отдельных участках магнитной цепи: U1м = H1l1м; Uδм = Hδδ; U2м = H2l2м; F1 = w1I1 и F2 = w2I2; F = F1 – F2 = w1I1 – w2I2. F1 и F2 – МДС обмоток. Сформулируем второй закон Кирхгофа: алгебраическая сумма МДС катушек в замкнутой магнитной цепи (контуре) равна алгебраической сумме магнитных напряжений вдоль этой цепи. 5.4. Расчет неразветвленных магнитных цепей Как отмечалось, магнитные цепи в практических устройствах обычно содержат участки из ферромагнетиков, магнитная проницаемость µa которых зависит от напряжённости магнитного поля Н, и воздушные промежутки с постоянной проницаемостью µ0. Зависимость магнитной индукции от напряжённости магнитного поля B(H) в ферромагнетиках нелинейная, поэтому магнитные цепи, как правило, являются нелинейными и все расчёты устройств с ферромагнетиками ведут с определённой степенью точности (в зависимости от упрощений при линеаризации кривой В = ƒ(Н) и т. п.). В практических расчётах неразветвлённой магнитной цепи часто пренебрегают магнитными потоками рассеяния и учитывают только магнитный поток вдоль основной магнитной цепи, принимая его неизменным во всех её сечениях. Всю МДС вдоль замкнутой магнитной цепи представляют в виде алгебраической суммы МДС на отдельных разнородных участках магнитной цепи, т.к. интеграл вдоль замкнутого пути может быть представлен в виде суммы интегралов отдельных участков этого пути. В силу малости воздушных промежутков в простых магнитных цепях часто пренебрегают «выпучиванием» в них магнитного поля, считая поперечное сечение магнитного потока в зазоре таким же, как в магнитопроводе, или увеличивая его сечение на 10…20% по сравнению с сечением, например, полюсов электромагнита при его длине δ > 0,1lм, где lм – ширина (или диаметр) магнитопровода. В сложных магнитных цепях нельзя пренебрегать потоками рассеяния и магнитным состоянием ферромагнетиков при неоднородном намагничивании: магнитную цепь приходится рассматривать как цепь с распределёнными параметрами, используя методы расчёта электромагнитных полей, в том числе метод последовательных приближений, метод конечных элементов и др. При расчёте неразветвлённой магнитной цепи различают так называемую прямую задачу (задачу синтеза) и обратную (задачу анализа магнитной цепи). Прямая задача
З Примем S1 ≈ Sδ и определим магнитную индукцию на участках цепи: B1 = Ф/S1; Bδ = Ф/Sδ; B1 = Bδ. Напряжённость магнитного поля на участке lм найдем по кривой намагничивания; например, для стали 1411 при B1 = 1,4 Тл, H1 ≈ 1200 А/м (рис. 5.7б); для воздушного зазора напряжённость Hδ ≈ 8·105Bδ. Согласно закону полного тока МДС обмотки с числом витков w: F = H1lм + Hδδ = wI.
В Обратная задача Заданы геометрические размеры магнитопровода: lм, δ, S1 ≈ Sδ и кривые намагничивания ферромагнетиков отдельных участков цепи (см. рис. 5.7), а также МДС F обмотки. Нуж-но определить магнитный поток Ф в зазоре. Запишем закон полного тока: H1lм + Hδδ = F = RмэФ = wI.
О Полученное нелинейное относительно магнитного потока Ф уравнение обычно решают на ЭВМ, выражая зависимость µ(Ф) в аналитической или табличной форме. Приближенное решение можно получит посредством графо-аналитических методов. Метод последовательного приближения. В первом приближении примем магнитное сопротивление цепи Rмэ, равное магнитному сопротивлению воздушного зазора, т.е.
П Ф0 = F/Rδм > Ф. Примем Ф1 = 0,7Ф0 и определим по методике прямой задачи величину F1, затем примем Ф2 = 0,8Ф0 и определим F2. Если F2 < F, то примем Ф3 > Ф2, например, Ф3 ≈ 0,9Ф0 и определим F3, и т.д. (до 5-6 значений потока Ф). Строим вебер-амперную характеристику Ф(F) цепи (рис. 5.8) и, проведя вертикальную линию с точки F (заданной МДС) до пересечения с кривой Ф = ƒ(F), а затем горизонтальную линию с этой точки до оси ординат, находим на оси ординат искомый магнитный поток Ф. Графический метод. Вычерчиваем схему замещения исследуемой цепи (см. рис. 5.9а) с выделением участка с линейным магнитным сопротивлением Rδм и участка с нелинейным сопротивлением R1м. МДС схемы замещения F = ФRδм + ФR1м = Uδм + U1м,
О
– нелинейная зависимость Ф = ƒ(U1м).
С Затем из точки F = Uм восстанавливаем перпендикуляр до пересечения с пунктирной кривой Ф(Uм) и на оси ординат находим искомый магнитный поток Ф. На практике поступают проще. Анализ выражения магнитного потока Ф = (F – U1м)/Rδм показывает, что U1м = F при Ф = 0 и U1м = 0 при Ф = F / Rδм = Ф0 (рис. 5.9в). Прямая, соединяющая две точки Ф0 и F, пересекает кривую Ф(U1м) в точке а, горизонталь через которую дает на оси ординат искомый магнитный поток Ф, а вертикаль позволяет определить на оси абсцисс магнитные напряжения U1м и Uδм.
Демонстрация электрических аппаратов и реле Электрическим аппаратом называют устройство, предназначенное для коммутации электрических, механических (электромагнитные муфты, которые соединяют или разъединяют ведомые и ведущие валы в механическом проводе), или других цепей путём замыкания или размыкания соответствующих связей.. В технике связи, радиотехнических и электронно-вычислительных системах наиболее широкое применение находят аппараты, коммутирующие электрические цепи: реле, контакторы, автоматические выключатели, пускатели, командные аппараты, рубильники, предохранители и др.
1 ).
2 Электромагнитный контактор (рис. 5.51) имеет втягивающую катушку 1, подвижный якорь 2, сердечник 3, систему главных контактов, состоящую из неподвижных 4 и подвижных 5 контактов, устройство для дугогашения (на рисунке не показано), демпфирующую пружину 6, гибкий токопровод 7 и часто снабжается комплектом вспомогательных контактов. Основными величинами, характеризующими контактор, помимо номинального тока (согласно ряду: 20, 40, 63, 75, 100, 160, 250, 400 А и т. д.), являются: время срабатывания (0,06…0,32 с), время отпускания якоря (0,03…0,5 с) и напряжение втягивающей катушки (24…380 В).
3 Механическая износостойкость пускателей составляет (5...16)106 включений c частотой 600…1200 включений в час. Номинальные коммутируемые токи при напряжениях 380/500 В от 3/1,5 до 146/80 А. Пускатель (рис. 5.52 )состоит из неподвижных 1 и подвижных 2 мостиковых контактов, контактной пружины 3, изоляционной стенки дугогасительной камеры 4, траверсы 5, якоря 6, магнитопровода 7 и катушки 8 тягового электромагнита, амортизационной пружины 9, теплового реле 10, возвратной пружины 11, вспомогательных контактов 12 и короткозамкнутого витка 13, расположенного на магнитопроводе 7. Для уменьшения потерь в сердечнике на вихревые токи и перемагничивание магнитопровод и якорь собраны из листов электротехнической стали.
ВОПРСЫ ДЛЯ САМОКОНТРОЛЯ 1. В каких единицах измеряется магнитное сопротивление и магнитное напряжение в схемах замещения магнитных цепей? 2. Чем обусловлена нелинейность магнитных цепей? 3. Как изменяется (увеличивается или уменьшается) индуктивность катушки при увеличении длины воздушного зазора в магнитопроводе, на котором она размещена? 4. Почему при расчёте магнитной цепи, участки которой находятся в режиме насыщения, нельзя пренебрегать потоками рассеяния? 5. При проведении опыта с катушкой со сталью равномерно увеличивали действующее значение тока. Нарисуйте качественные графики изменения магнитного потока в магнитопроводе при отсутствии воздушного зазора и с воздушным промежутком в магнитопроводе. 6. Каково соотношение между индуктивностью катушки с числом витков w и магнитным сопротивлением однородного магитопровода, на котором размещена катушка? 7. Зависит ли индуктивность катушки с ферромагнитным сердечником от частоты протекающего в ней тока? 8. Какой из материалов в большой степени подходит для изготовления постоянных магнитов? 9. Как будет изменяться напряжённость магнитного поля и магнитная индукция в постоянном магните, если уменьшить величину зазора посредством введения в него пластины из магнитно-мягкого материала? 10. Запишите закон Ома для участка магнитной цепи и законы Кирхгофа для разветвлённой магнитной цепи постоянного магнитного потока. 11. Определите отношение магнитных сопротивлений ферромагнитного участка длиной 20 см и воздушного зазора длиной 0,1 мм, сделав допущение, что вещество сердечника намагничено равномерно (µа = 100µ0) и что в силу малости воздушного промежутка магнитный поток в нём проходит через сечение, равное сечению сердечника. 12. Объясните физическую природу потерь в ферромагнитном сердечнике.
|
|

 магнитные
цепи, в которых магнитный поток
создается постоянным или переменным
током, протекающим в одной или нескольких
обмотках, размещённых на ферромагнитных
сердечниках.
магнитные
цепи, в которых магнитный поток
создается постоянным или переменным
током, протекающим в одной или нескольких
обмотках, размещённых на ферромагнитных
сердечниках.
 акон
электромагнитной индукции
Фарадея-Максвелла гласит,
что
при изменении магнитного поля,
связанного с витками катушки, в
последней наводится электродвижущая
сила (ЭДС)
индукции
акон
электромагнитной индукции
Фарадея-Максвелла гласит,
что
при изменении магнитного поля,
связанного с витками катушки, в
последней наводится электродвижущая
сила (ЭДС)
индукции ругими
словами, если перемещать
проводник в магнитном поле (то же, что
если проводник неподвижен, а магнитный
поток Ф изменяется во времени), в нем
наводится
ЭДС (направление
которой определяют по известному
правилу правой пуки), равная произведению
перпендикулярной к проводнику
составляющей магнитной
индукции B,
длине проводника l
и
скорости
его перемещения v,
т.е.
ругими
словами, если перемещать
проводник в магнитном поле (то же, что
если проводник неподвижен, а магнитный
поток Ф изменяется во времени), в нем
наводится
ЭДС (направление
которой определяют по известному
правилу правой пуки), равная произведению
перпендикулярной к проводнику
составляющей магнитной
индукции B,
длине проводника l
и
скорости
его перемещения v,
т.е. г
г де
F
− магнитодвижущая сила (МДС),
скалярная величина в амперах А]; −
полный
ток (алгебраическая
сумма токов) в контуре (ток Ik
берут со знаком «плюс», если его напра-
вление и направление обхода контура
при
интегрировании связаны правилом
правоходового винта, и наоборот); w
− число токов, пересекающих контур.
де
F
− магнитодвижущая сила (МДС),
скалярная величина в амперах А]; −
полный
ток (алгебраическая
сумма токов) в контуре (ток Ik
берут со знаком «плюс», если его напра-
вление и направление обхода контура
при
интегрировании связаны правилом
правоходового винта, и наоборот); w
− число токов, пересекающих контур.
 апишем
закон полного тока для отрезка a-b
контура (рис. 5.3):
апишем
закон полного тока для отрезка a-b
контура (рис. 5.3):

 акон
Ома для магнитной цепи.
Запишем
закон полного тока для однородной
магнитной цепи (рис. 5.4) с параметрами:
lм
– средняя длина магнитной силовой
линии (м. с. л.), м; S1
–
площадь сечения ферромагнитного
сердечника, м2;
I –
постоянный ток в катушке с числом
витков w
и найдём
магнитный поток Ф в
сердечнике (потоками рассеяния
пренебрегаем):
акон
Ома для магнитной цепи.
Запишем
закон полного тока для однородной
магнитной цепи (рис. 5.4) с параметрами:
lм
– средняя длина магнитной силовой
линии (м. с. л.), м; S1
–
площадь сечения ферромагнитного
сердечника, м2;
I –
постоянный ток в катушке с числом
витков w
и найдём
магнитный поток Ф в
сердечнике (потоками рассеяния
пренебрегаем):

 ткуда
получим выражение
ткуда
получим выражение
 де
F = wI
[А] – МДС
катушки;
де
F = wI
[А] – МДС
катушки;
 апишем
первый закон Кирхгофа для
условного узла 1
магнитной цепи (рис. 5.5):
апишем
первый закон Кирхгофа для
условного узла 1
магнитной цепи (рис. 5.5): 1l1м
+ H2l2м
+ Hδδ
= w1I1
– w2I2.
1l1м
+ H2l2м
+ Hδδ
= w1I1
– w2I2. аданы
геометрические размеры магнитной
цепи (lм,
δ, S1,
рис. 5,7а)
и магнитные свойства отдельных её
участков – кривые намагничивания
В(Н)
(рис. 5.7б),
например, все они изготовлены из
электротехнической стали 1411. Нужно
определить МДС F
обмотки,
необходимую для создания магнитного
потока Ф в зазоре.
аданы
геометрические размеры магнитной
цепи (lм,
δ, S1,
рис. 5,7а)
и магнитные свойства отдельных её
участков – кривые намагничивания
В(Н)
(рис. 5.7б),
например, все они изготовлены из
электротехнической стали 1411. Нужно
определить МДС F
обмотки,
необходимую для создания магнитного
потока Ф в зазоре. ыбрав
значение тока I,
определяют
число
витков w
катушки,
или,
наоборот, выбрав число витков
w катушки,
находят значение тока I.
ыбрав
значение тока I,
определяют
число
витков w
катушки,
или,
наоборот, выбрав число витков
w катушки,
находят значение тока I. ткуда
искомый магнитный поток
ткуда
искомый магнитный поток
 ри
этом условии возбуждаемый известной
МДС F
магнитный поток Ф0
в магнитопроводе заведомо больше
действительного, т.е.
ри
этом условии возбуждаемый известной
МДС F
магнитный поток Ф0
в магнитопроводе заведомо больше
действительного, т.е. ткуда
– линейная зависимость
Ф = ƒ(Uδм);
ткуда
– линейная зависимость
Ф = ƒ(Uδм);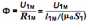
 троим
на одном рисунке (в выбранном масштабе)
три графика (рис. 5.9б):
Ф(Uδм)
для воздушного зазора – прямую линию,
угол наклона к оси абсцисс которой
пропорционален сопротивлению Rδм;
Ф(U1м)
для магнитной цепи без воздушного
зазора – кривую, подобную графику
B(H)
материала, так как поток Ф = BSм
пропорционален индукции В,
а магнитное напряжение Uм
=
Hlм
– напряжённости H,
и график Ф(Uм),
откладывая от оси ординат по горизонталям
отрезки, равные суммарной длине
отрезков кривой Ф(U1м)
и прямой Ф(Uδм).
троим
на одном рисунке (в выбранном масштабе)
три графика (рис. 5.9б):
Ф(Uδм)
для воздушного зазора – прямую линию,
угол наклона к оси абсцисс которой
пропорционален сопротивлению Rδм;
Ф(U1м)
для магнитной цепи без воздушного
зазора – кривую, подобную графику
B(H)
материала, так как поток Ф = BSм
пропорционален индукции В,
а магнитное напряжение Uм
=
Hlм
– напряжённости H,
и график Ф(Uм),
откладывая от оси ординат по горизонталям
отрезки, равные суммарной длине
отрезков кривой Ф(U1м)
и прямой Ф(Uδм).




 .
Электромагнитные реле. По
принципу действия различают
электромагнитные реле нейтральные
постоянного и переменного тока и
поляризованные.
По
характеру движения якоря электромагнитные
реле делятся на три
группы:
поворотные (рис. 5.49а),
с втяжным якорем (рис. 5.49б)
и язычкового типа (рис. 5.49в).
.
Электромагнитные реле. По
принципу действия различают
электромагнитные реле нейтральные
постоянного и переменного тока и
поляризованные.
По
характеру движения якоря электромагнитные
реле делятся на три
группы:
поворотные (рис. 5.49а),
с втяжным якорем (рис. 5.49б)
и язычкового типа (рис. 5.49в). .
Контакторы. Частые
включения
и
выключения мощных электрических цепей
и электрических машин с напряжением
до 500…600 В при нормальном режиме работы
обычно производятся электромагнитными
контакторами
– выключателями с электромагнитным
управлением.
.
Контакторы. Частые
включения
и
выключения мощных электрических цепей
и электрических машин с напряжением
до 500…600 В при нормальном режиме работы
обычно производятся электромагнитными
контакторами
– выключателями с электромагнитным
управлением.
 .
Магнитные пускатели.
Наиболее
распространенные магнитные
пускатели
(объединяющие контакторы и тепловые
реле) серий
ПМЕ, ПМА, ПА, ПВМ с управлением на
переменном токе имеют реверсивные и
нереверсивные исполнения и предназначены
для
управления электродвигателями.
.
Магнитные пускатели.
Наиболее
распространенные магнитные
пускатели
(объединяющие контакторы и тепловые
реле) серий
ПМЕ, ПМА, ПА, ПВМ с управлением на
переменном токе имеют реверсивные и
нереверсивные исполнения и предназначены
для
управления электродвигателями.