Тема 2

ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ

СИНУСОИДАЛЬНОГО ТОКА (6 ч)

Тема 2, содержание которой излагается в течение трех лекций, посвящена ана­лизу и расчёту линейных цепей синусоидального тока с использованием векторных диаграмм и комплексных амплитуд. Рассмотрены резонансные цепи, даны основы теории четырёхполюсников, в качестве которых обычно представляют усилители, фильтры, трансформаторы, лилии связи и другие устройства. Отмечены особенности расчёта индуктивно связанных и трёхфазных цепей. Дано понятие трёхфазной системы электроснабжения потребителей.

Тема изобилует интерактивными упражнениями и заданиями. По окончании её изучения предлагается провести (само)тестирование для оценки уровня своих учебных достижений по теме 2.

СОДЕРЖАНИЕ

Установочная лекция 3 (2 ч.)

АНАЛИЗ И РАСЧЕТ ОДНОФАЗНЫХ ЦЕПЕЙ ПЕРЕМЕННОГО ТОКА

Дидактические единицы:

3.1. Способы представления и параметры синусоидальных тока, напряжения и ЭДС.

3.2. Электрические цепи с элементами R, L и С.

3.3. Последовательная RLC-цепь и разветвленные цепи.

3.4. Мощности цепи переменного тока.

3.5. Коэффициент мощности.

3.1. Способы представления и параметры

синусоидальных ЭДС, напряжения и тока

ЭДС, напряжения и токи, значения которых периодически изменяются во времени по синусоидальному закону, называют синусоидальными (гармоническими, иногда их называют просто – переменными).

По сравнению с постоянным током синусоидальный ток имеет ряд преимуществ. В частности, производство, передача и использование электрической энергии наиболее эконо­мичны при синусоидальном токе; в цепях синусоидального тока относительно просто преобразовывать форму напряжения, а также создавать трехфазные системы напряжения. Синусоидальные токи широко используют в радио-, связной и контрольно-измери­тельной технике и в других областях.

В зависимости от типа решаемой задачи синусоидальные функции представляют:

 в виде аналитических выражений:

, , ,

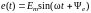где е, u, i  соответственно мгновенные значения ЭДС, напряжения, тока; E_m, U_m, I_m и t + _e, t + _u, t + _i  амплитуды и аргументы (фазы) синусоидальных функций;  = 2f и f =1/Т = = /2  угловая  (в рад/с) и циклическая f (в Гц) частоты колебаний ЭДС, напряжения и тока; Т = 2/ (в секундах) и  (в радианах) – период и начальная фаза колебаний синусоидальной функции;

 графически, посредством временной (рис. 2.1а) или вектор­ной (рис. 2.1б) диаграмм.

При вращении векторов U_m и I_m, отображающих синусоидальные функции u(t) и i(t) в плоскости x–y c угловой частотой  против хода часовой стрелки угол сдвига фаз  = _u – _i (в радианах или в градусах) между ними ос­та­ёт­ся неиз­мен­ным (см. рис. 3.1а), поэтому при построении векторной диаграммы векторы обычно изобра­жают не враща­ющимися, а неподвижными для момента времени t = 0 (t = 0) (см. рис. 3.1б), так как взаимное расположение векторов в плоскости х-у зависит не от фаз (начальных фаз), а от угла сдвига фаз .

Сдвиг фаз   алгебраическая ве­ли­­чина. Знак угла  на векторных диаграммах определяют по направлению отсчёта угла  от вектора тока I_m к век­тору напряжения U_m: если ука­занное направление угла  совпадает с направ­ле­нием частоты  вращения векторов на ВД, то угол  берётся со знаком плюс (рис. 3.1б), если направ­ление отсчёта угла  сов­падает с направлением хода часовой стрелки, то угол  берётся со знаком минус.

Отметим, что неподвижные векторы определяют два параметра си­ну­­со­идальных функ­ций: амплитуды и начальные фазы. Трет­ий параметр  угловая частота   должен быть известен.

Среди важнейших параметров анализируемых синусоидальных функций отметим их сред­ние в ин­тер­вале времени T/2 значения:

и среднеквадратичные значение за время Т  действующие ток, напряжение и ЭДС:

,

, .

При анализе сложных разветвленных цепей, в том числе и трехфазных цепей, синусоидально изменяющиеся электрические величины представляют в виде комплексных функций (комплексных чисел), изо­бра­жая векторы в комплексной плоскости с осями координат: Re  ось дей­стви­­­тель­ных чисел и величин и Im  ось мнимых чисел и величин (рис. 3.2).

При этом вектор U_m при t = 0 выражают экспоненциальной функцией с мнимым аргументом и называют комплексной амплитудой, т.е. .

При повороте вектора U_m на угол t его умножают на оператор вращения , т.е. при t 0

Запишем соответствие синусоидального напряжения и его комплекса:

u(t) = ,

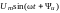
где  комплексная амплитуда напряжения, не завися­щая от вре­мени (t = 0); j = =  мнимая единица; U_m и _u  модуль и аргу­мент комплексной амплиту­ды напряжения U_m при t = 0; t + _u  ар­гу­мент комплекса амплитуды нап­ря­жения при t 0.

Отметим, что модулем комплек­сной амплитуды напряжения являет­ся амплитуда U_m, а аргументом  начальная фаза _u синусоидаль­ного на­пря­жения u(t). Умножение вектора U_m на множитель озна­чает его по­во­рот на угол t в положительном направ­лении (см. рис. 3.2б), в то время как при его умножении на множитель вектор U_m нужно повернуть на угол t по ходу часовой стрелки.

Лю­бая точ­ка в комплексной плоскости или вектор A = 1, направленный от начала ко­ор­ди­нат к данной точке, изображается комплексным числом A = a + jb, где а = 1coswt  ко­­орди­ната точки по оси действительных чисел; b = 1sinwt – координата то­ч­ки по оси мнимых чисел (рис. 3.3а).

Воспользовавшись формулой Эйлера

запишем координаты комплекса ампли­ту­ды напря­­жения на осях Re и Im комплексной плоскости (рис. 3.3б):

Полученное соотношение показывает, что синусоидальная функция напряжения u(t) = = U_msin(t + _u) есть проекция вращающегося вектора на мнимую ось, или есть мнимая часть (без j) комп­ле­ксной амплитуды напряжения, так как

а косинусоидальная функция напряжения u(t) = U_mcos(t + _u) есть проекция вращающегося вектора на действительную ось или действитель­­ная часть ком­­­плексной амплитуды напряжения, так как

Например, u = 10sin (t + 45)

где  комплексная амплитуда напряжения.

Поделив комплексную амплитуду напряжения U_m на , получим ком­­плекс действу­ю­щего значения напряжения или комплекс напряжения:

=

Обратный переход от комплексов к синусо­идаль­ным фун­кциям осуществляют следующим образом:

u(t) = U sin(t + _u ), i(t) = I_msin(t + _i) и т. д.

3.2. Анализ цепей с элементами r, l и с

методом векторных диаграмм

При анализе цепей гармонического тока угловая частота  = 2f пита­ющего цепь напряжения 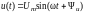, как правило, известна. В этом случае задачей расчёта цепи сину­соидального тока является определение амплитуд (или действующих значений) и началь­ных фаз токов и напряжений ветвей.

Руководствуясь ком­по­нентными уравнениями элементов схе­мы цепи:

­

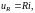
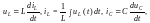
и записав для неё уравнения законов Кирхгофа, получают систему интегрально-диф­фе­рен­ци­аль­ных уравнений типа

причём правая часть этих уравнений содержит гармонические функции времени, а в левой части уравнений каждая синусо­идально изменяющаяся величина (при заданной угловой частоте ) содержит два неизвестных параметра (амплиту­ду и начальную фазу).

Следовательно, задача анализа линейной электрической цепи в ус­та­новившемся режиме при гармоническом воз­действии сводится к решению сис­темы линейных дифференци­аль­ных ура­внений с пос­тоян­­ными коэф­фициентами, правыми частями кото­рых яв­ляются гармони­ческие функции времени одной и той же частоты.

Р ассмотрим последовательную RL-цепь (рис. 3.4a), к зажимам кото­рой прил­­ожено изменяющееся по гармоническо­му за­ко­ну напряжение . Найдём ток i (его ам­­­­плитуду I_m и начальную фазу _i).

Согласно 2ЗК име­ем , где . Тогда

Получили линейное неоднородное дифферен­ци­аль­ное ура­в­­нение пер­вого порядка с гармониче­ской функцией в правой части. Частное решение уравне­ния при t =  будем искать в виде где  = _u  _i; в данном случае _i = .

Подставив выражение тока в дифференциальное уравнение, получим

или

Пер­вое слагаемое есть напряжение u_R на резисторе, ампли­ту­да кото­ро­го , а сдвиг фаз между напряже­ни­ем u_R и током i,  т.е. ток i в резисторе совпадает по фазе с напряжением u_R (рис. 3.4б, в).

Во втором слагаемом u_L уравнения (амплитуда . Откуда ам­плиту­да тока , где X_L = L = 2fL  реактивное индуктивное сопротивление (в омах) индуктивной катуш­ки, прямо пропорциональное частоте .

Разность фаз между напряжением u_L и током i = i_L (рис. 3.4б, в)

 = _u  _I =  + /2 +  = /2 (90),

т .е. ток i_L в индуктивном элементе отстаёт от напряжения u_L по фа­зе на угол /2 (или напряжение u_L опережает по фазе ток i_L на угол /2).

В полученном уравнении U_m = U_mR + U_mL две неизвестные величины: амплитуда тока I_m и угол сдвига фаз  между напря­же­нием u(t) и током i(t), значения которых можно определить, построив век­тор­­ную диаграмму тока и напряжений цепи (рис. 3.6а).

Получили треугольник напряжений. Применив теорему Пифагора

,

получим амплитуда тока ,

где  полное сопротивле­ние RL-цепи.

Второй искомый пара­метр тока  началь­ную фазу  _i =  опреде­лим из тре­угольни­ка сопротив­ле­­ний (рис. 3.6б), который получен из треуголь­ника напря­жений посредством деления всех его сторон (векторов) на вектор тока I_m:



т.е. ток i(t) в RL-цепи отстаёт по фазе от прило­жен­ного к цепи нап­ряжения u(t) на угол .

Поделив на левую и правую части выражения I_m = U_m/Z, получим соотношение для действующих значений тока и напряже­ния на входе RL-цепи (рис. 3.6в)

Применив рассмотренную методику анализа цепи методом векторных диаграмм:

а) согласно второму закону Кирхгофа записывают интегрально-диф­фе­рен­циальное урав­не­ние цепи;

б) решение уравнения ищут в виде ;

в) подставив выражение тока i(t) в уравнение, уточняют фазы напря­жений на элемен­тах R, L, С и на других элементах;

г) строят векторную диаграмму напряжений, начиная с вектора тока I_m (при t = 0), и треугольник сопротивлений цепи; далее, вычисляют полное сопротивление Z, ам­плитуду тока I_m, его начальную фазу _i и сдвиг фаз  между нап­ря­жением u(t) и то­ком i(t) на входе цепи,

к последовательной RC-цепи (рис. 3.7), получим:

а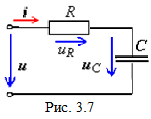 ) дифференциальное уравнение состояния цепи , а после подстановки выражения тока и преобразования

или

,

в котором амплитуда напряжения на конденсаторе ,

где  реактивное ёмкостное сопротивление,

в) сдвиг фаз между напряжением u_C(t) и током i_С(t) в ёмкостном эле­менте (рис. 3.8а)

    =

т .е. ток i(t) = i_С(t) в ёмкостном элементе опережает напряжение u_С(t) по фа­­зе на угол /2 (рис. 3.8б и в).

г) построив ВД тока и напряжений, получили вектор напряжение на входе цепи (рис. 3.9а)

И з век­торной диаг­рам­мы следует, что ток i(t) в RC-цепи опережа­ет прило­жен­ное к цепи напряжение u(t) по фазе на угол .

Векторная диаграмма для действующих значений напряжений и тока представлена на рис. 3.9б.

Из треугольников напряжений (рис. 3.9а и б) имеем

,

откуда амплитуда и действующее значение искомого тока

I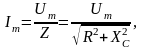 = , где  полное сопротивление RC-цепи.

Из треугольника сопротивлений (рис. 3.9в) RC-цепи определим угол сдвига фаз

 ,

откуда следует, что значение ёмкостного сопротивления X_C в формулах расчёта токов в ветвях цепей нужно подставлять со зна­ком минус.