Семинар 5 Распределение Больцмана

Добавил:

AnonimusPro Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный технологический университет "Станкин"

Предмет:

Физика

Файл:

поэтому число Авогадро NA с учетом (15.5)

.pdf

Скачиваний:

Добавлен:

10.01.2021

Размер:

257.4 Кб

Скачать

☆

g(x, y, z) ce

5. Распределение Больцмана

Если равновесный идеальный газ с температурой Т находится во внешнем поле консервативной силы, его одночастичная функция распределения в координатном подпространстве фазового пространства имеет вид

пот( x, y, z ) kT .

Здесь пот(x, y, z) – потенциальная энергия частицы, связанная с внешней

консервативной силой, k – постоянная Больцмана и с – постоянная, определяемая условием нормировки функции распределения

g(x, y, z)dxdydz c e				п о т ( x, y, z )	dxdydz 1	,
g(x, y, z)dxdydz c e				kT	dxdydz 1	,
				kT
V		V
где V – объем области, в которой находятся частицы.
Отсюда получаем, что
с		1			.

	e	п о т ( x, y, z )
		п о т ( x, y, z )
		kT	dxdydz
		kT

Данное распределение называется распределением Больцмана.

Изменения во времени координат и скоростей частиц при тепловом движении являются независимыми случайными процессами, поэтому полная одночастичная функция распределения по координатам и скоростям есть произведение функция распределения Больцмана и Максвелла

				пот( x, y, z)			кин		пол
(x, y, z;	,	,	) c e		с e			сe		,
				kT			kT		kT
x	y	z	Б			М
где пол пот(x, y, z) кин –		полная		энергия		частицы,				равная сумме еѐ

потенциальной и кинетической энергий, а нормальная постоянная с сБ сМ , сБ и сМ – нормировочные постоянные распределений Больцмана и Максвелла.

Задача №13 Определить среднюю тепловую энергию одномерного

классического гармонического осциллятора в состоянии равновесия с температурой Т.

Решение Пусть осциллятор совершает гармонические колебания вдоль оси х и

точка х=0 определяет его устойчивое положение равновесия. Средняя тепловая энергия гармонического осциллятора

		m 2	x2
кин	пот	x		,	(13.1)
кин	пот	2	2	,	(13.1)
		2	2

m – масса осциллятора и к>0 – постоянная, определяющая возвращающую силу Fвоз x . Частота колебаний осциллятора 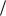m .

В состоянии теплового равновесия распределение по скоростям х даѐтся законом Максвелла

1 2

m x2

f ( x )

2kT ,

(13.2)

2 kT

а распределение по координате х – законом Больцмана

1 2

x 2

g(x)

2kT .

(13.3)

2kT

Следовательно,

1 2

m ч2

1 2

3 2

ч2

ч2e

2kT

u2e u

2kT d x

2kT

1 2

2kT 3 2 3 4

2kT

1 2

x 2

2kT dx

2 kT

и средняя полная энергия (13.1) теплового движения осциллятора принимает вид

2 du

(13.4)

(13.5)

гармонического

kT .

(13.6)

Отметим, что в полном соответствии с законом о равнораспределении средней кинетической энергии теплового движения по всем степеням свободы

кин 12 kT ,

причем для гармонического осциллятора

кин пот .

Ответ: kT .

	Задача №14
Определить среднюю потенциальную энергию пот		молекул азота N2
	const ) поле силы тяжести Земли,	если температура
в однородном ( g

атмосферы Т считается постоянной по всей высоте. Решение

Распределение молекул азота по высоте во внешнем поле консервативной силы тяжести описывается законом Больцмана

g(z) ce	mgz
g(z) ce	kT ,	(14.1)

где m – масса молекулы азота, g – ускорение свободного падения, ось z направлена вертикально вверх, mgz – потенциальная энергия молекулы азота

на высоте z, z 0 соответствует	поверхности Земли и						с –	постоянная,
определяемая из условия нормировки:
		mgz
g(z)dz c e			dz c	kT	e u du c	kT	1	(14.2)
		kT
				mg		mg
0	0				0

пот

c	mg	.	(14.3)

	kT

С учетом (14.1) и (14.3) средняя потенциальная энергия молекулы азота

пот mgz g(z)dz mg

mg ze mgzkT dz mg kT 0

mg kT 2 kT . kT mg

mg kT	2
		ue u du


kT mg		0

(14.4)

Если температура атмосферы повышается, средняя кинетическая энергия теплового движения молекул азота увеличивается и соответственно увеличивается вероятность их нахождения на большей высоте, что приводит к росту средней потенциальной энергии.

Ответ: kT .

Задача №15

Для определения числа Авогадро NA Ф. Перрен измерял распределение по высоте одинаковых сферических частиц гуммигута, взвешенных в воде.

Он нашел, что при радиусе	частиц	r 0,212 мкм,	плотности гуммигута
1,194 г/см3, плотности	воды	0 1 г/см3 и	температуре воды

t 18o C отношение чисел частиц в слоях воды, отстоящих друг от друга по высоте на l 30мкм, равно 2,08 . На основании приведенных данных оцените число Авогадро.

Решение В состоянии теплового равновесия распределение числа частиц

гуммигута по высоте z описывается законом Больцмана

	N (z) N0e			п о т( z )				(15.1)
	N (z) N0e			kT	,			(15.1)
				kT
где N0 0 – постоянная,
		0				0
	пот(z) mg	0	mg z		1	0	mgz	(15.2)
	пот(z) mg		mg z		1		mgz	(15.2)

– потенциальная энергия частиц с учетом как силы тяжести, так и выталкивающей силы, определяемой законом Архимеда, и

	m				4	r3								(15.3)
	m					r3								(15.3)
			3
– масса одной сферической частицы.
Согласно условиям задачи и (15.1) - (15.3)
											0	mgl
			N (z)						1
									1

								e				kT	,	(15.4)
								e				kT	,	(15.4)
		N (z l)
что позволяет найти постоянную Больцмана
k 1	0		4	r3				gl		1,07 10 23 Дж К .				(15.5)
k 1				r3						1,07 10 23 Дж К .				(15.5)
			3				ln T
			3				ln T

Известная универсальная газовая постоянная

что достаточно близко к современному значению 6,022 1023 1/моль.

Ответ: NA 7,76 1023 1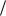 моль .

Соседние файлы в предмете Физика

#
10.01.2021313.57 Кб3Семинар 3 Механика.pdf
#
10.01.2021208.42 Кб7Семинар 3. Уравнение Ван-дер-Ваальса.pdf
#
10.01.2021367.65 Кб3Семинар 4 Механика.pdf
#
10.01.2021265.01 Кб4Семинар 4 Распределение Максвелла.pdf
#
10.01.2021241.79 Кб2Семинар 5 Механика.pdf
#
10.01.2021257.4 Кб2Семинар 5 Распределение Больцмана.pdf
#
10.01.2021260.82 Кб2Семинар 6 Механика.pdf
#
10.01.2021211.98 Кб2Семинар 6 Процессы переноса.pdf