Семинар 4 Механика
.pdf
Семинар №4
Затухающие колебания с вязким трением. Вынужденные колебания и явление резонанса
Рассмотренные на семинаре №3 свободные незатухающие гармонические колебания происходят в малой окрестности устойчивого положения равновесия под действием консервативной возвращающей силы ,величина которой линейно растѐт со смещением частицы относительно положения равновесия.
Если учесть действия на частицу силы вязкого трения
|
|
|
|
|
Fв.тр. Г , |
(4.0.1) |
|
- константа, зависящая от свойств частицы |
|||
где - скорость частицы и Г |
|||
и среды, то уравнение движения частицы вдоль оси х с учетом
возвращающей силы записывается следующим образом: |
(4.0.2) |
|
mx kx Гx 0 , |
||
|
|
|
где точка сверху означает производную смещения x по времени t .Смещение x отсчитывается от устойчивого положения равновесия частицы в точке x=0.
Уравнение движения гармонического осциллятора с вязким трением
можно записать в стандартной формуле: |
0 . |
(4.0.3) |
|||||||||
|
|
|
|
|
|
x 2 x 0 |
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
где |
2 |
1 |
и |
02 |
k |
. Это однородное обыкновенное |
дифференциальное |
||||
2m |
m |
||||||||||
|
|
|
|
|
|
|
|
|
|||
уравнение второго порядка по времени. Для однозначного решения данного уравнения необходимо в начальный момент времени задать два начальных условия: положение частицы и еѐ скорость.
|
Если |
выполняется |
условие |
0 , |
решение |
|
|
полученного |
|||||
дифференциального уравнения имеет вид: |
|
|
|
|
|
||||||||
|
|
|
|
|
|
x(t) A(t) cos( 1t 0 ) |
, |
|
|
|
(4.0.4) |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
A(t) A e t cos( t |
0 |
) |
и |
2 2 |
. Постоянные |
A 0 |
и |
0 |
находятся с |
|||
|
0 |
1 |
|
1 |
0 |
|
|
0 |
|
|
|||
помощью двух начальных условий.
Таким образом, наличие силы вязкости трения приводит к экспоненциальному уменьшению во времени амплитуды колебаний гармонического осциллятора и сдвигу частоты собственных колебаний. Полная механическая энергия гармонического осциллятора уменьшается во времени по экспоненциальному закону:
|
|
mx2 |
|
kx2 |
|
|
|
E(t) |
|
|
|
E 0 e 2 t , |
(4.0.5) |
|
2 |
2 |
||||
|
|
|
|
|
||
где |
- полная механическая энергия гармонического осциллятора в |
|||||
начальный момент времени и 0 |
(слабое затухание).Уменьшение во |
|||||
время амплитуды колебаний описывается с помощью коэффициента затухания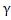 
и логарифмического декремента затухания
ln |
A(t) |
T0 |
, |
(4.0.6) |
|
|
|||||
A(t T0 ) |
|||||
|
|
|
|
23
где - период гармонических колебаний при |
|
и |
0 . |
|
|||
Уменьшение во время полной механической энергии гармонического |
|||||||
осциллятора определяется добротностью |
|
|
|
|
|
|
|
Q 2 |
E(t) |
|
|
|
|
, |
(4.0.7) |
E(t) E(t T ) |
|
T |
|
||||
|
|
|
|
|
|
||
|
0 |
|
0 |
|
|
|
|
где Е(t) –полная механическая энергии осциллятора в момент времени t и Механическая энергия преобразуется в энергию теплового движения
за счѐт работы силы вязкого трения.
Задача 10
Амплитуда гармонических колебаний груза массой m=0,1кг, подвешенного на пружине с жесткостью k=20Н/м уменьшилась в 2 раза за 1 минуту. Определите добротность Q этой колебательной системы.
Решение.
Согласно определению добротности Q как характеристики уменьшения во времени энергии Е колебательной системы
Q 2 |
|
|
E(t) |
|
|
, |
(4.1.1) |
|
|
|
|
|
|||
|
|
E(t T ) E(t) |
|
|
|||
|
|
||||||
|
|
|
0 |
|
|
|
|
где Е(t) – энергия колебательной системы в момент времени t, Т0 – период колебаний.
В случае слабого затухания, когда коэффициент затухания 0 , 0 2 / T0
- круговая частота колебаний, полная энергия уменьшается со временем по экспоненциальному закону
E(t) E e 2 t . |
(4.1.2) |
0 |
|
Здесь Е0 – энергия колебательной системы в момент времени t=0.
С помощью (4.1.2) выражение (4.1.1) для добротности преобразуется к виду
|
|
|
|
|
|
E0e 2 t |
1 |
|
|
|
2 |
|
|
|
|||||
|
|
Q 2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
. (4.1.3) |
|
|
|
|
E e 2 (t T0 ) E e 2 t |
|
|
|
|
e 2 T0 1 |
|
|
1 e 2 T0 |
T0 |
|||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
использовалась |
|
приближенная |
|
|
формула |
e 2 T0 1 2 T , |
поскольку |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
T |
2 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, для вычисления добротности необходимо найти |
|||||||||||||||||||
коэффициент затухания |
и период Т0 собственных колебаний груза. |
||||||||||||||||||
2. В случае слабого затухания смещение х гармонического осциллятора описывается формулой
x(t) a e t |
cos( t ) , |
(4.1.4) |
|
0 |
0 |
0 |
|
где |
|
|
|
a(t) a e t |
|
|
(4.1.5) |
0 |
|
|
|
– амплитуда колебаний и 0 – начальная фаза.
Согласно (4.1.5) амплитуды колебаний в произвольные моменты времени t1 и t2 связаны соотношением
24
|
a |
a e t1 |
|
, a |
a e t2 |
, |
|
a1 |
e (t2 t1 ) . |
(4.1.6) |
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||
|
1 |
0 |
|
|
|
|
2 |
|
0 |
|
|
|
|
|
|
|
a2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По условию задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
|
|
1 |
, t |
|
t t |
1мин, |
(4.1.7) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||
|
|
|
|
|
a2 |
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
поэтому получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
e (t2 t1 ) , |
|
|
|
|
|
(4.1.8) |
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
ln |
|
1 |
|
|
ln 2 ln e t |
t , |
(4.1.9) |
|||||||||||||||||||
|
|
2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ln 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
(4.1.10) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3) Период собственных колебаний груза, подвешенного на пружине, в |
||||||||||||||||||||||||||||||
случае слабого затухания описывается формулой |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
T 2 |
|
m |
. |
|
|
|
|
|
|
(4.1.11) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
4) С помощью формул (4.1.3), (4.1.10) и (4.1.11) получаем |
|
|||||||||||||||||||||||||||||
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Q |
|
1 |
|
|
k |
|
|
60 |
|
200 |
|
|
600 |
624 . |
|
|||||||||||||||
ln 2 2 m |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 ln 2 |
|
2 ln 2 |
|
|
|||||||||||||||||
Ответ: Q=624.
Вынужденные колебания. Предположим, что на частицу действуют три силы:
1)возвращающая сила F1 kx ;
2)сила вязкого трения F2 Г Гx ;
3)внешняя сила F3 , меняющаяся по гармоническому закону F0 cos t , где
F0 0 – постоянная амплитуда и - циклическая частота внешней силы. Уравнение движения гармонического осциллятора принимает вид
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
ma Fi |
|
|
|
|
|
(4.0.8) |
|||
|
|
|
i 1 |
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kx |
|
|
|
|
F0 cos |
|
(4.0.9) |
|
|
|
mx |
|
|
Гx |
|
t . |
||||
Разделив левую и правую части на m и сделав замены 2 Г m , 2 |
k m |
||||||||||
и f0 F0 m , получим дифференциальное уравнение в стандартной форме |
|||||||||||
|
|
2 |
|
f0 cos |
|
|
(4.0.10) |
||||
x |
2 x |
0 x |
|
|
t . |
||||||
Это неоднородное обыкновенное дифференциальное уравнение второго порядка. Неоднородность уравнения связанна с тем, что в него кроме
перемещения, скорости и ускорения ( x, x, x ) входит слагаемое |
f0 cos t , не |
|
|
зависящее от х. Общее решения однородного уравнения есть сумма общего решения однородного уравнения и частного решения неоднородного уравнения:
x(t) A e t cos( t |
) |
|
|
f0 |
|
|
cos( t ) , |
(4.0.11) |
||
|
|
|
|
|
||||||
0 |
0 |
0 |
|
|
( 2 |
2 )2 |
4 2 2 |
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
0 |
|
|
|
25
где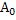 
и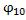
- постоянные, определяемые с помощью двух начальных условий, а 1 определяется выражением
|
tg 20 |
2 |
, |
20 0 . |
(4.0.12) |
|
|
||||
|
2 2 |
||||
|
|
0 |
|
|
|
При |
первым слагаемым, стоящим в правой части выражения x(t) и |
||||
описывающим собственные колебания гармонического осциллятора на частоте 0 , можно пренебречь и оставить только второе слагаемое, которое
описывает вынужденные колебания осциллятора на частоте внешней силы.
Зависимость амплитуды вынужденных колебаний от частоты внешней силы показана на рис. 4.1
Aвын |
|
|
|
f0 |
|
|
(4.0.12) |
|
|
|
|
|
|||
( 2 |
2 )2 |
|
|||||
|
|
|
4 2 2 |
||||
|
|
|
|
0 |
|
|
|
Рис. 4.1.
На частоте рез наблюдается явление резонанса – резкое возрастание
амплитуды вынужденных колебаний, которая принимает максимальное значение
A |
f0 |
QA . |
(4.0.12) |
|
|
||||
рез |
2 0 |
|
0 |
|
|
|
|
|
|
Здесь Q - добротность осциллятора и |
A |
f0 |
- смещение осциллятора под |
|
|
||||
|
1 |
02 |
|
|
действием постоянной силы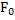 
. При резонансе сдвиг фаз между колебаниями осциллятора и внешней силы равен
|
. |
(4.0.13) |
1 рез |
2 |
|
|
|
Такой сдвиг фазы обеспечивает наибольшую эффективность передачи энергии от внешнего источника осциллятору.
Задача №11 Тело, подвешенное на пружине, имеет период собственных колебаний
T0 =1с. Величина силы вязкого трения пропорциональна скорости тела :
26
Fтр.вяз. Г , Г>0 – постоянный коэффициент. Если колебания тела
возбуждаются внешней гармонической силой с амплитудой F0 = 1Н, то амплитуда установившихся колебаний в резонансе Арез = 0,05м. Определите коэффициент Г в формуле для силы вязкого трения.
Решение.
1. Колебания тела, подвешенного на пружине, под действием силы тяжести, силы вязкого трения и внешней силы, меняющейся во времени по гармоническому закону, описываются неоднородным дифференциальным уравнением
(4.2.1)
где ось х направлена вертикально вниз, причем точка х=0 соответствует низшему концу пружины в свободном (недеформированном состоянии), g – ускорение свободного падения.
Перепишем уравнение (4.2.1) в стандартной форме
|
|
|
mx x kx mg F0 cos t |
(4.2.2) |
|||
|
|
|
|
|
|
|
|
или |
|
|
x 2 x 0 x g f0 cos t , |
(4.2.3) |
|||
|
|
|
|||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
где / 2m , 0 |
k / m и |
f0 |
Fo / m . |
|
|||
Общее решение х(t) |
уравнения (4.2.3) состоит из трех |
слагаемых, |
|||||
описывающих три разных движения тела под действием рассматриваемых сил:
x(t) x1 x2 (t) x3 (t) . |
(4.2.4) |
||
где |
|
|
|
x |
g |
|
(4.2.5) |
|
|||
1 |
2 |
|
|
|
|
||
|
0 |
|
|
– статическое смещение вниз конца пружины, определяющее положение
равновесия тела, в котором сила упругости пружины |
kx , уравновешивает |
||
силу тяжести mg , |
|
|
|
x |
a e t cos( 0 t ) |
(4.2.6) |
|
2 |
0 |
0 |
|
– динамическое смещение тела, связанное с его свободными (собственными) колебаниями,
x3 Acos( t 0 ) |
(4.2.7) |
– динамическое смещение тела, связанное |
с его вынужденными |
колебаниями.
Амплитуда А вынужденных колебаний определяется формулой
A |
|
|
|
|
|
F0 / m |
|
|
. |
|
(4.2.8) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
( 2 |
2 )2 |
4 2 2 |
||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
При резонансе, когда частота ω внешней силы равна частоте |
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||
собственных колебаний |
0 |
k / m |
тела на пружине, амплитуда |
|||||||||||||
вынужденных колебаний принимает максимальное значение |
|
|||||||||||||||
A |
A |
|
|
|
F0 |
|
F0 |
|
F0T0 |
. |
(4.2.9) |
|||||
|
|
|
|
|
|
|||||||||||
max |
|
вын |
|
|
2 m 0 |
|
Г0 |
|
|
|
2Г |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
27
Отсюда получаем, что
Г |
F0T0 |
= 3,2 |
H c |
. |
(4.2.10) |
|
2 A |
|
м |
|
|
|
max |
|
|
|
|
Ответ: Г 3,2 Н с .
м
Задача №12 Неподвижное тело, подвешенное на пружине, увеличивает ее длину на
= 7 см. Считая массу пружины пренебрежимо малой, определите период Т0 малых вертикальных колебаний тела. Ускорение свободного падения g = 9,8м/с2. Сопротивление воздуха не учитывать.
Решение Уравнение движения тела под действием силы упругости пружины и силы тяжести имеет вид (см. решение задачи №17)
|
|
mx kx mg |
|
|
(4.3.1) |
|||
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
(4.3.2) |
|||
|
|
x 0 x g , |
|
|
||||
|
|
|
2 |
|
|
|
||
где 0 k / m . |
|
|
|
|
|
|||
Решение уравнения (4.3.2) записывается следующим образом |
|
|||||||
|
|
x(t) |
g |
|
a cos( t |
) . |
(4.3.3) |
|
|
|
|
|
|||||
|
|
|
2 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|||
Здесь первое слагаемое описывает статическое смещение нижнего конца пружины под действием веса тела, которое согласно условиям задачи равно
g |
|
(4.3.4) |
|
2 |
|||
|
|
||
0 |
|
|
Второе слагаемое в правой части (4.3.3) описывает собственные (свободные) колебания тела с периодом
T |
2 |
. |
(4.3.5) |
|
|||
0 |
0 |
|
|
|
|
||
Из формул (4.3.4) и (4.3.5) следует, что
|
|
|
|
T 2 |
0,53c . |
(4.3.6) |
|
0 |
g |
|
|
|
|
||
Ответ: T0 0,53c
28