МЭТ лабораторные / МЭТ_8_лаб_отчёт

Протокол

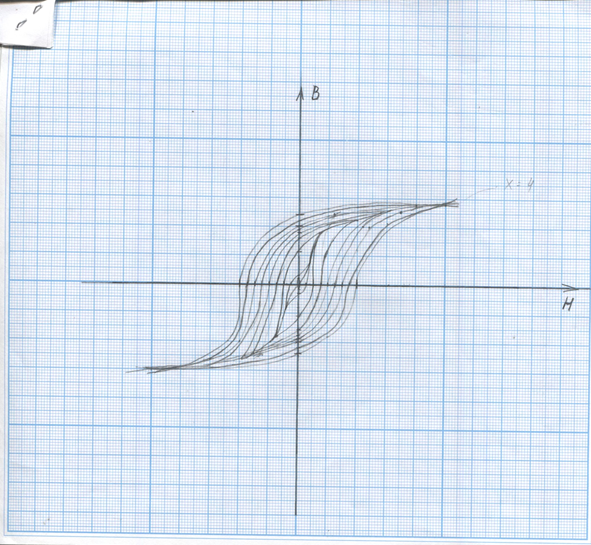
Обработка результатов

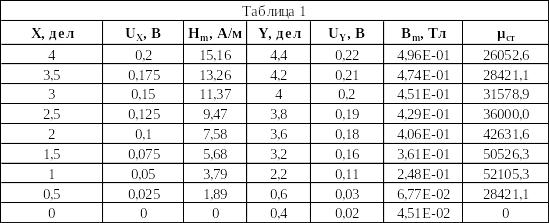
1. Рассчитать значения U_x и U_y, используя масштабы осей осциллографа m_x = m_y = 0,05 В; вычислить H_m и B_m при R_T = 10 Ом, r_ср = 0,021 м, w₁ = 100, w₂ = 1330, C_и = 10^-6 Ф, R_и = 300 кОм, S = 1‧ 10^-4 м^-2. Найти статическую магнитную проницаемость μ_ст.

Примеры расчёта:

U_x = X ‧ m_x = 4 ‧ 0,05 В = 0,2 В; U_y = Y ‧ m_y = 4,4 ‧ 0,05 В = 0,22 В;

H_m = 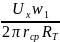= 0,2 ‧ 100 / (2 ‧ 3,14 ‧ 0,021 ‧ 10) = 20 / 1,3188 ≈ 15, 16 А / м

B_m = 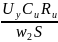= 0,22 ‧ 10^-6 ‧ 300 ‧ 10³ / (1330 ‧ 1‧ 10^-4) = 0,066 / 0,133 ≈ 4,96 ‧ 10^-1 Тл

μ_ст = B_m / (μ₀ ‧ H_m) = 4,96 ‧ 10^-1 / (4 ‧ 3,14 ‧ 10^-7 ‧ 15, 16) ≈ 4,96 ‧ 10^-1 / (0,19 ‧ 10^-4) = 26052,6

2. Построить на одном графике зависимости B_m(H_m) и μ_ст (H_m)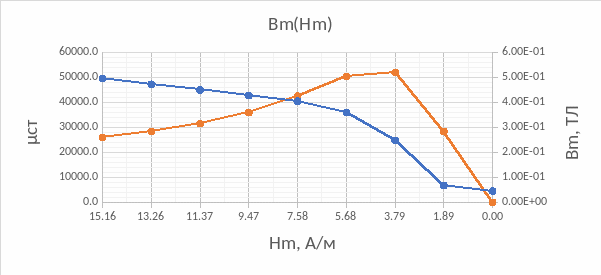

μ_ст(H_m) – оранжевым цветом

3. Рассчитать энергии магнитных потерь, соответствующие площадям предельных петель гистерезиса на разных частотах, в единице массы ферромагнитного материала за один цикл перемагничивания; d = 8600 кг / м³, где d – плотность исследуемого материала

Пример расчёта для f = 50 Гц:

h₁ = 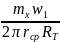= 0,05 ‧ 100 / (2 ‧ 3,14 ‧ 0,021 ‧ 10) = 5 / 1,3188 ≈ 3,79 А / м

b₁ = 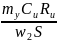= 0,05 ‧ 10^-6 ‧ 300 ‧ 10³ / (1330 ‧ 1‧ 10^-4) = 0,015 / 0,133 ≈ 0,113 Тл

Э = 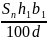= 5,88 ‧ 10^-2 ‧ 3,79 ‧ 0,113 / (100 ‧ 8600) ≈ 2,93 ‧ 10^-8 Дж / кг

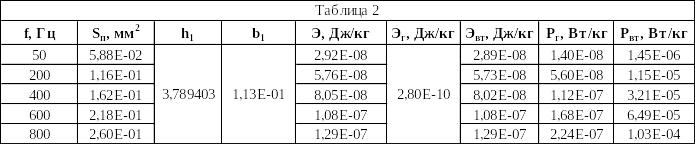
4. Построить частотную зависимость потерь энергии в образце в виде графика Э(f); найти потери на гистерезис Э_г и потери на вихревые токи Э_вт; рассчитать мощности потерь на гистерезис P_г и вихревые токи P_вт

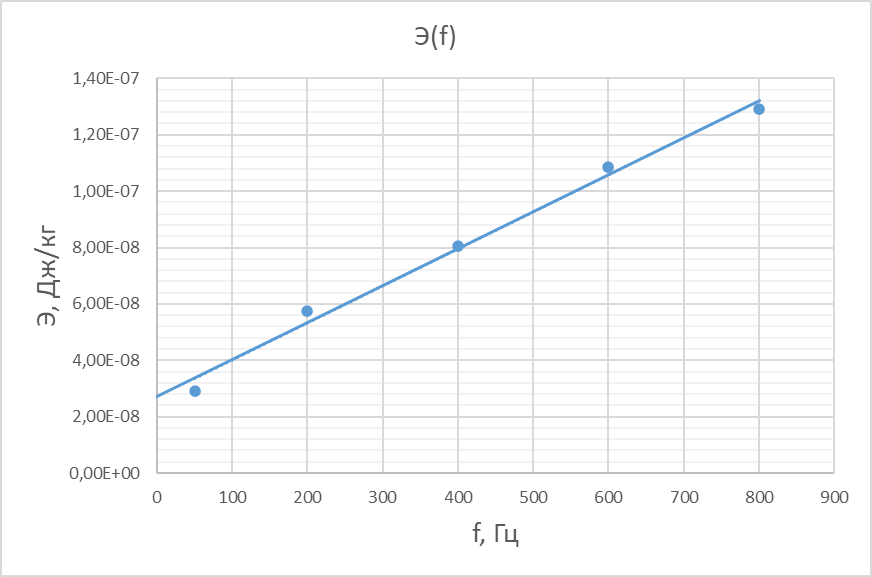
Пример расчёта для f = 50 Гц:

из графика Э(f) Э_г = 2,8 ‧ 10^-10 Дж / кг, тогда Э_вт = Э - Э_г = 2,92 ‧ 10^-8 - 2,8 ‧ 10^-10 = 2,892 ‧ 10^-8 Дж / кг;

P_г = Э_г ‧ f = 2,8 ‧ 10^-10 ‧ 50 = 1,4 ‧ 10^-8 Вт / кг

P_вт = Э_вт ‧ f = 2,892 ‧ 10^-8 ‧ 50 = 144,6 ‧ 10^-8 Вт / кг

См. таблицу 2 пункта 3.

5. Вычислить напряжение U_L на катушке индуктивности с испытуемым сердечником; найти индуктивность катушки L; определить эффективную магнитную проницаемость μ_эф.

Пример расчёта для f = 50 Гц:

U_L = 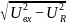= (580² – 30²)^1/2 = (335500)^1/2 ≈ 579,2 мВ

L = = = 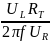579,2 ‧ 10 / (2 ‧ 3,14 ‧ 50 ‧ 30) = 5792 / 9420 ≈ 0,61 Гн

μ_эф = 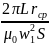= 0,61 ‧ 0,021 / (2 ‧ 10^-7 ‧ 100² ‧ 1‧ 10^-4) = 0,01281 / (2 ‧ 10^-7) ≈ 6,45 ‧ 10⁴

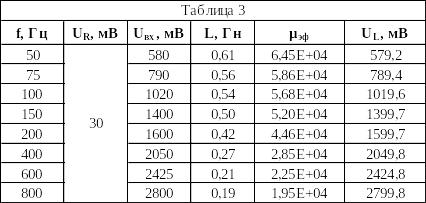
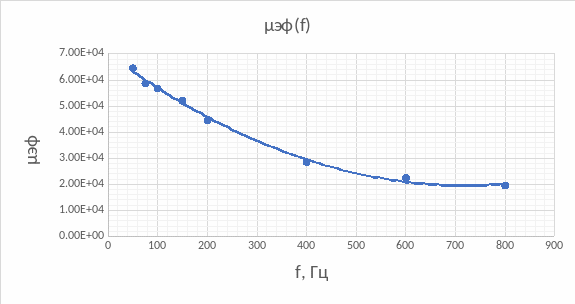
6. Построить зависимость μ_эф(f)

Вывод: в ходе лабораторной работы для железо-никелевого (пермалоя) сплава установлено, что:

1. при увеличении частоты (f) синусоидального сигнала возрастают потери энергии (Э) в образце (возрастают линейно, как видно из графика в пункте 4).

2. при увеличении напряжённости магнитного поля (H_m) статическая магнитная проницаемость μ_ст возрастает до некоторого значения (связано с увеличением относительного изменения объёмов соседних доменов за счёт смещения доменных границ и за счёт возрастания вклада процессов вращения векторов намагниченности) (μ_ст = 52105,3), а затем идёт на спад, вследствие насыщения магнитной индукцией.

3. при увеличении частоты (f) синусоидального сигнала μ_эф уменьшается (т. к. усиливаются вихревые токи, индуцируемые в сердечнике, что приводит к возрастанию размагничивающего потока) экспоненциально (похоже на экспоненциальную зависимость).