Вопрос №20. Наименьший и минимальный элемент множества относительно порядка
Наименьший элемент, минимальный элемент
Пусть на множестве А дан частичный порядок. Элемент у ∈ А называется наименьшим элементом множества А, если для любого элемента х ∈ А верно у ≤ х.
Элемент у ∈ А называется минимальным относительно заданного порядка А, если не существует таких элементов х ∈ А, что х < у.
Вопрос № 21. Наибольший и максимальный элементы множества относительно порядка
Наибольший элемент, максимальный элемент
Пусть на множестве А дан частичный порядок. Элемент у ∈ А называется наибольшим элементом множества А, если для любого элемента х ∈ А верно у ≥ х.
Элемент у ∈ А называется максимальным относительно заданного порядка А, если не существует таких элементов х ∈ А, что х > у.
В диаграмме Хассе вершина а ∈ Vа соответствует максимальному элементу, если из нее не выходит ни одна дуга.
Наибольший элемент является и максимальным элементом.
Наибольший элемент, если он есть, всегда единственный.
Максимальных элементов у множества может быть несколько.
Вопрос № 22. Вполне упорядоченное множество
Определение: Частично упорядоченное множество X называется вполне упорядоченным, если любое его непустое подмножество имеет минимальный элемент.
Теорема: Всякое вполне упорядоченное множество является линейно упорядоченным. Доказательство: Пусть А – вполне упорядоченное множество:
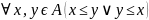
Тогда:
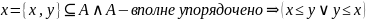Примеры:
1. Пустое множество является вполне упорядоченным. 2. Простейший пример бесконечного вполне упорядоченного множества — множество натуральных чисел с естественным упорядочением.
Вопрос №23. Верхняя граница множества Х, syp(X)=?
Пусть
А — частично упорядоченное множество.
Пусть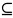 х
А. х
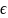А верхняя граница Х, если
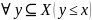
Верхние и нижние границы не обязаны существовать для любого множества и если существуют, то не всегда единственны. Если существует наименьшая верхняя граница, то она называется супремумом и обозначается syp(X).
Вопрос №24. Нижняя граница множества Х, inf X=?
Элемент x∈A называется нижней границей множества X, если для любого y∈X (x≤y)
Элемент x∈A называется наибольшей нижней гранью, если это наибольшая из нижних границ множества X (inf)
Вопрос №25. Определение графа ориентированного, неориентированного, смешанного, пустого
Граф, неориентированный граф, НГ, ориентированный граф, оргаф, ОГ, смешанный граф, пустой граф.
Вопрос №26. Степень вершины, псевдограф, мультиграф
Степенью вершины называется число ребер, которым принадлежит эта вершина. Если это количество четно, то вершина называется четной, в противном случае вершина называется нечетной.
Мультиграф
Определение. Неориентированный граф с кратными ребрами без петель называется мультиграфом. Несколько ребер, соединяющих одну и ту же пару вершин, называются кратными.
Для ориентированного графа имеем два случая: дуги, имеющие одно направление, называются кратными, разное направление – параллельными.
Ориентированный мультиграф — граф, соединяющий кратные дуги без петель.
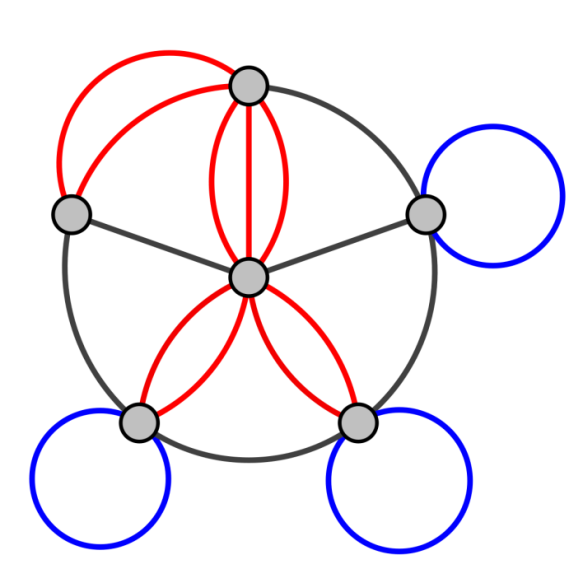
Псевдограф
Определение. Граф, содержащий петли и кратные ребра, называется псевдографом.
Петлей называется ребро, соединяющее вершину саму с собой.
При подсчете степени вершины петля учитывается дважды.
Для некоторых авторов, термины псевдограф и мультиграф являются синонимами. Для других, псевдограф является мультиграфом, которому разрешено иметь петли.
Синие линии – петли
Красные линии – кратные ребра
Вопрос №27. Изоморфные графы. Примеры. Гомеоморфизм графов.
Графы G1 = (V1, E1) и G2 = (V2, E2) называются изоморфными, если существует биекция φ между множеством вершин V1 и V2, сохраняющая смежность.
{L1, L2} ∈ E1 => {φ(L1), φ(L2)} ∈ E2.
Для орграфа:
(L1, L2) ∈ E1 => (φ(L1), φ(L2)) ∈ E2.
Для доказательства того, что графы изоморфны, достаточно указать отображения, удовлетворяющие условию, описанному в определении.
Чтобы доказать, что графы неизоморфны, достаточно найти какое-нибудь свойство, которым обладает один граф и не обладает другой, и которое у изоморфных графов должно быть общим.