Вопрос №1. Основные понятия интуитивной теории множеств. Множество. Понятие принадлежности. Интуитивный принцип объемности

Согласно Кантору, множество есть любое собрание определенных и различных между собой объектов нашей интуиции или интеллекта, мыслимое как единое целое. Множество – это совокупность объектов произвольной природы, рассматриваемых как единое целое.

Множества могут состоять из любых объектов, кроме того, сами множества могут быть элементами множества (допускает рассмотрение множеств, элементы которых нельзя точно указать, в первую очередь это бесконечное множество)

Понятие принадлежности. Смысл понятия принадлежности состоит в том, что, имея объект «а» и множество «А», мы всегда можем сказать, какое из утверждений верно:

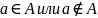
Интуитивный принцип объемности. Два множества «А» и «В» равны в том случае и только в том случае, когда о ни состоят из одних и тех же элементов.

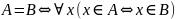
Этот принцип имеет два следствия:

1. Множества равны, если элемент обозначает один и тот же объект ( )

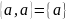2. Порядок, в котором перечисляются элементы множества, не важен.

Вопрос №2. Подмножество. Конечное, бесконечное и пустое множество. Способы задания множеств. Интуитивный принцип абстракции

Подмножество — множество A является подмножеством множества  B, если любой элемент, множества A является элементом множества  B. Пишут: A⊂B или A⊆B. Таким образом:

(A⊂B)⇔(x∈A⇒x∈B).

Конечное множество — множество А называется конечным, если оно состоит из конечного числа элементов. (Если у него нет равномощного собственного подмножества)

VB ((В С А & |В|= |А|) =>(В = А)).

Бесконечное множество - множество, не являющееся конечным. (Для конечного множества А используется запись |Л| < бесконечности. Все остальные множества называются бесконечными. Взяв отрицание условия конечности, получаем, что для бесконечного множества А:)

//ЭВ {В С A & |B| = |A| к В ф А),

Пустое множество - Множество, не содержащее ни одного элемента (множество мощности 0). Пустое множество является подмножеством любого множества.

Способы задания множеств –

1. Перечисление элементов: М: ={а, 6, с,..., z}; Множество цифр с 10 с.с.

2. Описание свойств множества:. М : = {х | Р{х)} ;

Интуитивный принцип абстракции:

Любое множество определяет некоторое свойство P(x) и всякое свойство P(x) задает некоторое множество.

Пример: P(x) = {x поступил в ИГЭУв 2008 г}

А = {x | P(x)}

Множество, состоящее из Х, заданное однозначно.

Вопрос №3. Парадокс Рассела. Его значение для теории множеств.

Поделим все множества на 2 класса:

• Множества, не содержащее себя в качестве элемента

• Множества, содержащее себя в качестве элемента

Пусть F – множество, содержащее все множества, относящиеся к первому классу.

F = {M | M ∉ M}

Является ли F элементом самого себя?

Если F ∈ F, то поскольку F содержит все такие же множества, которые не являются элементами самих себя, то F ∉ F.

Однако, если F ∉ F, то по построению F как раз содержит все такие же множества и значит

F ∈ F.

Нарушение принципа принадлежности. Мы не можем сказать какое утверждение верное.

Данный парадокс доказывает противоречие теории множеств. В математике подобные противоречия преодолевают в аксиоматической теории множеств. Для нас – интуитивная.