Вопрос №15. Разбиение множества а на классы. Теорема.

Классификация – это действие распределения объектов по классам на основании сходств объектов внутри класса и их отличия от объектов других классов.

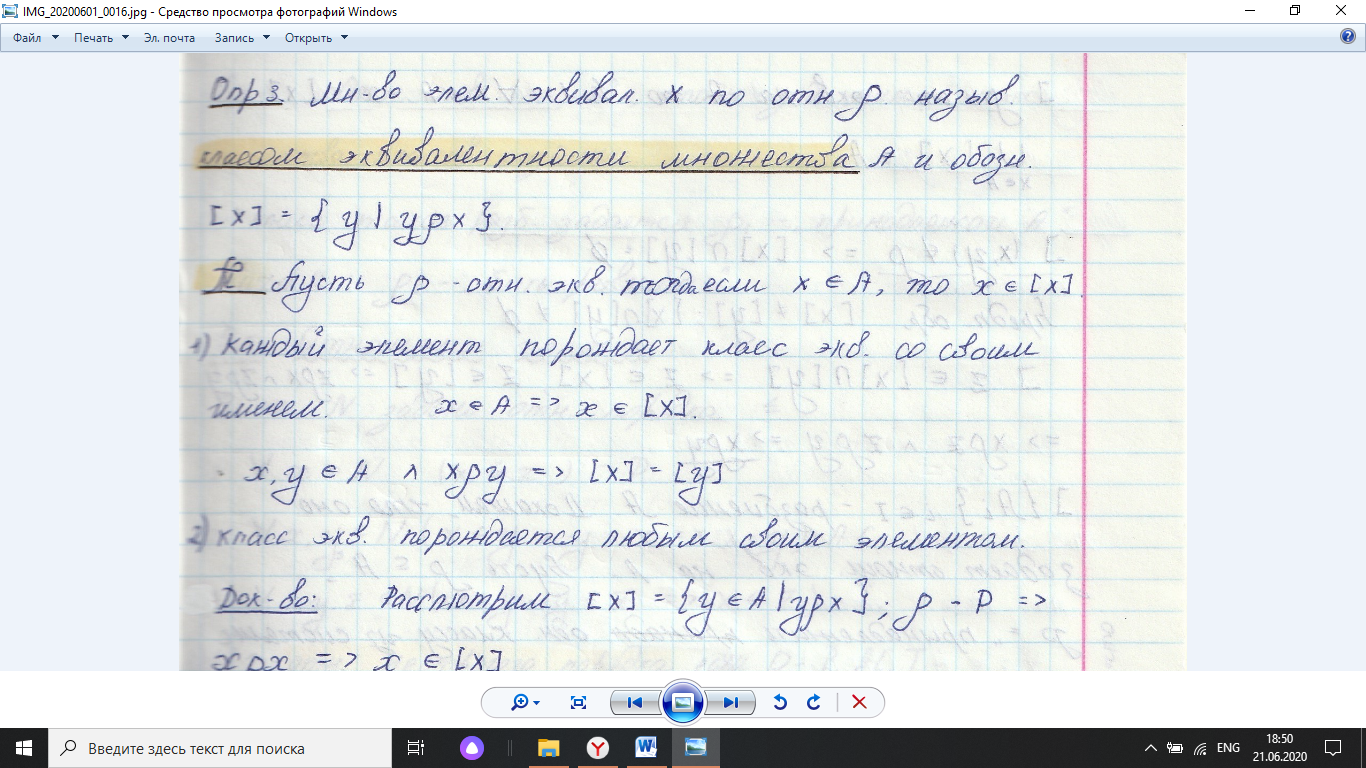
Определение:

Считают, что множество Х разбито на классы Х₁, Х₂,…,Х_п, если:

1. подмножества Х₁, Х₂,…,Х_п попарно не пересекаются;

2. объединение подмножеств Х₁, Х₂,…,Х_п совпадает с множеством Х.

Если не выполнено хотя бы одно из этих условий, классификацию считают неправильной.

Так, множество X треугольников можно разбить на три класса: остроугольные, прямоугольные и тупоугольные

Пример.

M есть множество всех учащихся в средних школах Москвы. Множество М можно разбить на попарно не пересекающиеся подмножества, например, следующими двумя способами:

1). мы объединяем в одно слагаемое всех учащихся одной и той же школы (то есть разбиваем множество всех учащихся по школам);

2). мы объединяем в одно слагаемое всех учащихся одного и того же класса (хотя бы и разных школ).

Теорема 1.

Пусть дано отображение f множества A на множество B. Полные прообразы f^-1(b) всевозможных точек b множества B образуют разбиение множества A на классы. Множество этих классов находится во взаимно однозначном соответствии с множеством B.

Теоремы 2.

Пусть дано разбиение множества А на классы. Это разбиение порождает отображение множества A на некоторое множество B, а именно на множество B всех классов данного разбиения. Это отображение получается, если заставить соответствовать каждому элементу множество A тот класс, к которому он принадлежит.

1. Вопрос №16. Фундаментальная теорема арифметики

Вопрос №17. Отношения порядка

Антисимметричное транзитивное отношение называется отношением порядка.

1) Отношение p подмножества А^2 называется отношением нестрогого порядка, если оно Р, АС, Т.

• отношения на числовом множестве

• отношение «быть не ниже по должности» на множестве преподавателей университета

• отношение ⊆ на булеане Р(I): A ⊆ B («A нестрого включено в B»)

2) Отношение p подмножества А^2 называется отношением строгого порядка, если оно АР, АС, Т.

• отношения на числовом множестве

• отношение «быть старше» на множестве людей

• отношение ⊂ на булеане Р(I): A ⊂ B («A строго включено в B»)

3) Порядок р называется линейным, если любая пара элементов из множества А сравнима по порядку р.

4) Порядок р называется частичным, если он не является линейным.

Таким образом, каждое отношение порядка имеет две характеристики:

Характеристики отношения порядка:

• первая связана с рефлексивностью отношения (Р – нестрогий порядок, АР – строгий порядок)

• вторая связана со сравнением элементов по порядку (все сравнимы – линейный порядок, не все – частичный порядок)

Множество, на котором задано отношение частичного порядка, называется частично упорядоченным.

Множество, на котором задано отношение линейного порядка, называется линейно упорядоченным.