Вопрос №39. Взвешенные графы. Задача о кратчайшем соединении. Алгоритм Краскала.
Взвешенный граф
Иногда в задаче каждому ребру соответствует некоторый параметр - длина ребра или стоимость прохождения по нему. В терминологии графов такой параметр называется весом ребра, а граф, содержащий взвешенные рёбра, взвешенным.
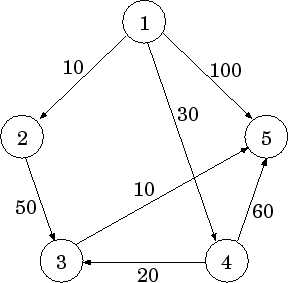
Рис 1. Пример взвешенного графа
Типичная задача для таких графов - поиск кратчайшего пути. Например, в этом графе кратчайший путь между вершинами 1 и 5: 1−4−3−5, так как его вес равен 30+20+10=60, а вес ребра 1−5 равен 100.
Вес графа — сумма весов всех ребер, входящих в граф.
Алгоритм Краскала
Из всех ребер, входящих в граф, выбираем ребро li с минимальным весом, которое не является петлей. Если таких ребер несколько — выбираем любое.
Добавляем ребро lk ∈ E\{l1, l2, …, lk-1 }, где l1, l2, …, lk-1 — ребра. (выбираем на предыдущих шагах по следующим правилам:
А) добавление ребра lk l1, l2, …, lk-1 не должно приводить к образованию цикла.
Б) Из всех возможных ребер lk удовлетворяющих пункту А выбираем ребро наименьшего веса. Повторяем пункт 2 до тех пор, пока не решим задачу.
Алгоритм краскала работает тогда, когда часть дорог между городами уже построена, т.о. вес этих дорог = 0, а дальше по алгоритму.
Пример выполнения алгоритма Краскала
Рис 2. Исходный граф.
Выбираем и отмечаем дуги с наименьшим весом (1). Таких дуг у нас будет 2: (0,6) и (1,5). Для них не появляется цикл в графе, поэтому эти дуги мы оставляем.
Рис 3. Граф после 1 шага.
Дальше выбираем дуги с весом 2. Таких у нас 1 штука – (0,10). Если мы выберем эту дугу, то цикл в графе не появляется. Значит, её мы оставляем.
Рис 4. Граф после 2 шага.
Выбираем дуги весом 3. Таких у нас 4 штуки: (2,7), (3,9), (5,6), (6,10). Для трёх дуг цикл не образуется, но для дуги (6,10) образуется цикл: 0 – 10 – 6 – 0. Поэтому эту дугу мы вычёркиваем.
Рис 5. Граф после 3 шага
Выберем и отметим дуги весом 5. Таких у нас 3 штуки: (10,2), (5,3), (7,3). Мы выберем только первые две, так как третья дуга (7,3) нам не подходит, ибо она образует цикл: 0-10-2-7-3-5-6-0. Поэтому эту дугу мы удаляем.
Рис 6. Граф после 4 шага
Выберем и отметим дуги весом 7. У нас таких 2 штуки: (4,3), (6,8). Обе эти дуги нам подходят, ибо циклы не образуются.
Рис 7. Граф после 5 шага
Выберем и отметим дуги весом 11. Таких у нас 2: (1,0) и (2,4). Обе не подходят, ибо каждая из них образует цикл. Так дуга (1,0) образует цикл 0 – 6 – 5 – 1 – 0, а дуга (2,4) образует цикл 2 – 4 – 3 – 5 – 6 – 0 – 10 – 2. Значит, мы их вычёркиваем.
Рис 8. Граф после 6 шага.
Выберем и отметим дуги весом 14. Таких у нас всего 1 штука: (5,4). Эта дуга не подходит так из-за неё образуется цикл 5 – 4 – 3 – 5. Значит, её мы тоже удаляем.
Рис 9. Граф после 7 шага
Выберем и отметим дуги весом 15. Таких у нас 2 штуки: (10,8), (9,10). Они обе не подходят, так как они образуют циклы. Так дуга (10,8) образует цикл 0 – 10 – 8 – 6 – 0, а дуга (9,8) образует цикл 5 – 6 – 8 – 9 – 3 – 5. Следовательно, и эти 2 дуги мы удаляем.
Рис 10. Полученное минимальное остовное дерево
Мы получили минимальное остовное дерево для нашего графа, и его вес равен 37. На данном моменте алгоритм заканчивается.