Вопрос №36. Матрица достижимости, сильно связности. Пример. Компонент связности

Матрицей достижимости орграфа D называется квадратная матрица T(D) порядка n, где:

Аналогично определяется понятие матрицы достижимости для неорграфа.

Говорят, что на множестве вершин, графа D введено отношение достижимости ρ, если:

ρ ↔ ∃ путь из в

(путь - незамкнутый ориентированный маршрут, в котором все дуги попарно различны).

Матрица достижимости T(D) находится по формуле:

), где E единичная матрица

Матрица сильной связности орграфа D называется квадратная матрица S(D) порядка n, где:

Для неорграфа G матрицу сильной связности можно определить как

Матрица сильной связности S(D) находится по формуле:

1∧1=1, в других случаях – 0

Пример:

)

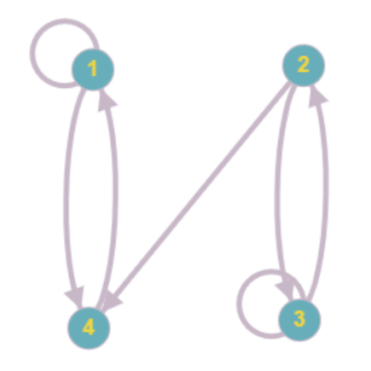
Если , то достижима из

Если , то не достижима из

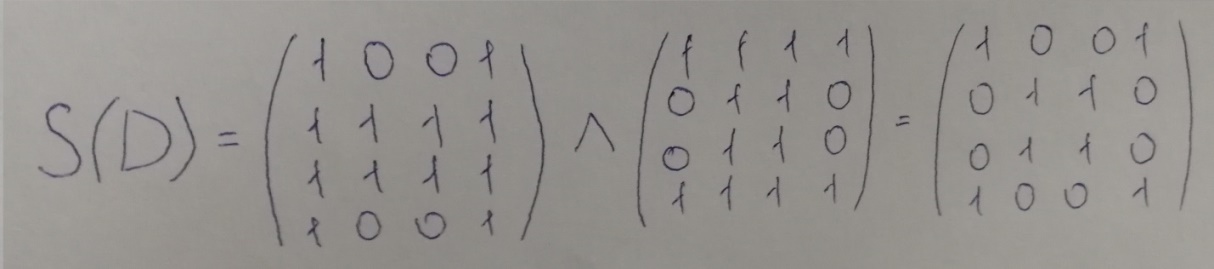
Компонентом связности (сильной связности) графа G (орграфа D) называется его связный (сильно связный) подграф, не являющийся собственным подграфом никакого другого связного (сильно связного) подграфа графа G (орграфа D).

Вопрос №37. Гамильтоновы графы. Теоремы

Гамильтонова цепь – простая цепь, проходящая через все вершины данного графа только один раз

Гамильтонов цикл – простой цикл, проходящий через все вершины (исключая начальную) данного графа только один раз

Гамильтонов граф – граф, который имеет гамильтонов цикл

Полугамильтонов граф – граф, который имеет гамильтонову цепь

Гамильтонов путь – путь в ориентированном графе, S={x₁, x₂, …, x_n}, проходящий через все вершины графа, притом только по одному разу.

Гамильтонов контур – контур, M={x₁, x₂, …,x_n, x₁} в ориентированном графе G(X), если он проходит через все вершины графа, притом только по одному разу.

Замечания.

1. Гамильтонов цикл содержит все вершины графа по одному разу, но не обязательно содержит все ребра графа.

2. Любой граф G можно превратить в гамильтонов, добавив достаточное количество вершин и ребер, соединяющих эти новые вершины между собой и с некоторыми из старых.

1. Теорема Кёнига. В полном конечном графе всегда существует гамильтонов путь.

2. Если в простом графе с n вершинами n ≥ 3 для G — гамильтонов граф.

Вопрос № 38.Эйлеровы графы (теорема). Полуэйлеровы графы

1. ЭЙЛЕРОВ ГРАФ — связанный граф, в котором существует замкнутая цепь, соединяющая все ребра графа.

Эйлеров путь/цикл — путь/цикл, соединяющий все ребра (дуги) графа.

ТЕОРЕМА: Необходимое и достаточное условие

Связанный неориентированный мультиграф (с кратными ребрами без петель) является эйлеровым если каждая его вершина имеет четную степень.

________________________________________________________________

Эйлеров цикл (для неориент. Графа) – существует тогда и только тогда, когда отсутствуют вершины нечетных степеней.

Эйлеров цикл (для ориентир. Графа) – цикл, который проходит ровно один раз по каждому ребру.

Эйлерова цепь (для ориент. Графа) – цепь, проходящая через каждое ребро ровно 1 раз.

Эйлерова цепь (для неориент. Гарфа) – существует тогда и только тогда, когда в ней есть ровно 2 вершины нечетной степени.

________________________________________________________________

2. ПОЛУЭЙЛЕРОВЫЙ ГРАФ – граф, содержащий незамкнутую цепь, которая проходит все ребра по одному разу.

Данный связный граф будет полуэйлеровым тогда и только тогда, когда в точности 2 вершины будут нечетными, а степени остальных вершин – четными.

На рис. 3 изображены: а – эйлеров граф, б – полуэйлеров граф и в – граф, не являющийся ни эйлеровым, ни полуэйлеровым