1. Примеры:

1. Граф G и H – изоморфны.

2. Графы и изоморфны. Действительно, отображения и ( ) взаимно-однозначны и удовлетворяют условию, описанному в определении изоморфных графов.

3. Графы ниже не изоморфные, хотя набор степеней вершин совпадает.

2. Гомеоморфизм графов:

Орграфы G1 и G2 называются гомеоморфными, если существуют их подразделения, являющиеся изоморфными. Два графа являются гомеоморфными, если либо один из них — подграф другого, либо существует граф, являющийся подграфом обоих графов.

Вопрос №28. Маршрут, ориентированный маршрут, длина маршрута, замкнутый маршрут. Цепь. Простая цепь, путь, простой путь, цикл, простой цикл (контур). Пример. Маршрут

Неориентированный маршрут (или просто маршрут ) - это чередующаяся последовательность   вершин и ребер графа, такая, что для каждого   выполняется одно из двух:   или  . 

Ориентированный маршрут

Маршрут называется ориентированным (или ормаршрутом ), если   для каждого  . Таким образом, при движении вдоль маршрута в орграфе ребра могут проходиться как в направлении ориентации, так и в обратном направлении, а при движении вдоль ормаршрута - только в направлении ориентации.

Длина маршрута – число рёбер маршрута

Замкнутый маршрут – это маршрут, начальная вершина которого совпадает с конечной вершиной. В противном случае (если начальная и конечная вершина не совпадают) маршрут называется открытым.

Цепь – это незамкнутый маршрут, все рёбра (дуги) которого различны (не повторяются).

Простая цепь – это цепь, все вершины которой попарно различны.

Путь – незамкнутый ориентированный маршрут, где все дуги попарно различны.

Простой путь – путь, проходящий через любую вершину не более одного раза.

– замкнутый маршрут, где все ребра попарно различны.

Контур - замкнутый ориентированный маршрут, дуги которого попарно различны.

Простой цикл (контур) – цикл (контур), в котором все вершины, кроме начальной и конечной, попарно различны.

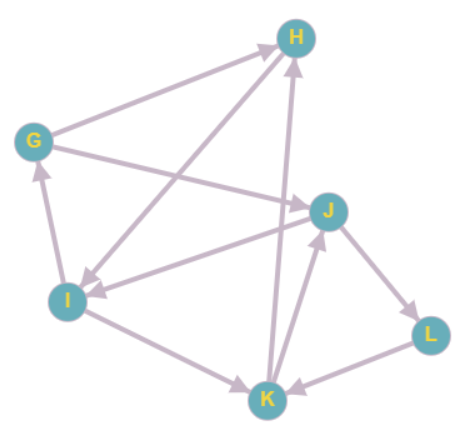
Пример:

Путь: GHIKJL, JLKHIKJ.

Простой путь: KHIGJ, LKJI.

Цикл: HIKJLH, IKJLKHI.

Простой цикл (контур): GJLKIG, GHI.

Вопрос №29. Связные вершины. Связный граф. Орграф сильно связный, односторонне связный, слабо связный, несвязный

Связанные вершины – 2 вершины называются связанными, если существует маршрут соединяющий их.

Связный граф — это граф, у которого любые две вершины связанны.

Орграф называется сильно связным, или сильным, если любая пара его вершин Vi и Vj соединены путем.

Орграф называется односторонне связным, или односторонним, если для любой пары его вершин Vi и Vj существует хотя бы один из путей Vi —> Vj или Vj —> Vi.

Орграф называется слабо связным, или слабым, если для любых двух различных вершин графа существует, по крайней мере, один маршрут, соединяющий их

Орграф называется несвязным, если для некоторой пары вершин орграфа не существует маршрута, соединяющего их.

Вопрос №30. Простой неориентированный граф. Теорема о сумме степеней всех вершин. Теорема о числе вершин в простом полном неориентированном графе

Простой неориентированный граф – это неориентированный граф, в котором нет петель и кратных ребер.

Теорема 1. В простом неориентированном графе G сумма степеней всех вершин четна и равна удвоенному числу ребер.

Док-во: сумма степеней всех вершин графа равна количеству всех концов ребер, которые есть в графе. Но у каждого ребра 2 конца, значит общее кол-во ребер в 2 раза меньше количества всех концов ребер, теорема доказана.

Теорема 2: В простом неориентированном графе G число вершин с нечетной степенью четно.

Док-во: Действительно, если бы нечетных вершин в графе было бы нечетное число, то сумма степеней всех нечетных вершин выражалась бы нечетным числом. А сумма степеней любого количества четных вершин выражается четным числом. Поэтому сумма степеней всех вершин графа будет нечетным числом, что противоречит предыдущему замечанию.