Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

4781

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

1.71 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Вариант 18.

Вариант 19.

Вариант 20.

Вариант 21.

Вариант 22.

Вариант 23.

Вариант 24.

Вариант 25.

Задача № 7.

Вариант 1.

Вариант 3.

Вариант 5.

Вариант 7.

Вариант 9.

Вариант 11.

Вариант 13.


y 3 ln			x2	1 ,	2 x 3 .
								3	.
y 1 x2			arcsin x,			0 x		3
y 1 x2			arcsin x,			0 x		4
								4
y 2 ln sin x ,						x	.
					3		2
y2 x 1 3 ,				1 x 2 .

y ln	x2	1 , 3			x 4 .
x2 y2 25.
y 7 ln sin x ,						x	.
					3		2

3y2 x 1 3 , 1 x 2 .

Исследовать на сходимость несобственный интеграл.

1 dx

x2 .

1 x2 .

1 dx

0 x .

xe x2 dx .

arctgx dx .

0 1 x2

1		x2dx
			.


0	1 x6
		x2dx
					.
	x3 3			2
0

Вариант 2.

Вариант 4.

Вариант 6.

Вариант 8.

Вариант 10.

Вариант 12.

Вариант 14.

0 dx

4 x2 .

2	dx
	dx
			.
	x2	4	.
0

x2 e x3 dx .

e	ln x dx
	ln x dx					.
						.
0				x
0
e			dx
			dx
					.
	x ln x				.
1
1				xdx
				xdx				.


0			1 x2
1			xdx
			xdx				.


0		1 x4

Вариант 15.

Вариант 17.

Вариант 19.

Вариант 21.

Вариант 23.

Вариант 25.

		dx
		dx
					.
	4 x2				.
0

		dx	.
		x2	.
1
e		dx
		dx
							.
	x ln2 x						.
1
0		dx
		dx
				.
	9 x2			.

		dx
		dx
						.
	16 x2					.

e ln2 x dx

0 x .

Вариант 16.

Вариант 18.

Вариант 20.

Вариант 22.

Вариант 24.

	x2dx
			.
	x3 3	3	.
0	x3 3

xex2 dx .

3		dx
		dx
				.
	x2 9			.
0
			e2 xdx
							.
		e2 x 2				3	.
0		e2 x 2

2			xdx
			xdx		.


			4 x4
1			4 x4

Задача № 8. Вычислить приближѐнно определѐнный интеграл с помощью формулы прямоугольников, формулы трапеций и формулы Симпсона, разбив отрезок интегрирования на n частей. Все вычисления производить с точностью до 0,001.

	8			1
Вариант 1.	4 1 x3 dx, n 8.		Вариант 2.		4 x3 dx, n 10.
	0			0
	9			4
Вариант 3.		16 x2 dx, n 10.	Вариант 4.	4		64 x3 dx, n 8.
	1			4
	2			1
Вариант 5.		4 8 x3 dx, n 8.	Вариант 6.		9 x3 dx, n 10 .
	6			0
	10			5
Вариант 7.		18 x2 dx, n 10.	Вариант 8.	4		27 x3 dx, n 8.
	0			3
	0			3
Вариант 9.		4 1 x3 dx, n 8 .	Вариант 10.		4 27 x2 dx, n 8 .

	0			0
Вариант 11.		4 x2 9 dx, n 8 .	Вариант 12.		4 4 x2 dx, n 10 .
	8			2
	2			1
Вариант 13.	4	8 x3 dx, n 10 .	Вариант 14.		1 x3 dx, n 10 .

Вариант 15. 4x2 16 dx, n 10 .

Вариант 17. 4 x3 dx, n 8.

Вариант 19. 464 x3 dx, n 10 .

Вариант 21. 9 x3 dx, n 10 .

Вариант 23. 427 x3 dx, n 10 .

Вариант 25. 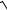18 x2 dx, n 10 .

Вариант 16. 41 x3 dx, n 10 .

Вариант 18. 16 x2 dx, n 10 .

Вариант 20. 48 x3 dx, n 10 .

Вариант 22. 41 x3 dx, n 8 .

Вариант 24. 427 x2 dx, n 10.

	5
	6
Вариант .	4 9 x2 dx,	n 8
	2

2.3. Образец решения РГР.

Задача № 1. Найти неопределенные интегралы.


1. Вычислить интеграл	x5 x		x 2	dx .
1. Вычислить интеграл				dx .
		x

Преобразуем подынтегральную функцию:

x5 x

x 2

x4 x2

x x 2

Тогда

dx = x4

dx = x4dx

1dx

x2 dx 2 x =

			3
	x5	x2
	x5	x2
=				2ln	x	C .
=	5	3		2ln	x	C .

		2
		2

При вычислении использовали свойства неопределѐнного интеграла:

а)

f1(x) f2 (x) dx f1(x)dx f2 (x)dx ,

б)

Cf (x)dx C f (x)dx ,

и табличные интегралы 1)

и 2).

Вычислить интеграл

x 3 5 x2 dx .

Делаем замену

5 x2 t ,

тогда

2xdx dt и

xdx

dt . Следовательно,

5 x2 t

3 5 x2 4

x 3 5 x2 dx =

t 3 dt

C =

C .

xdx 2 dt

Вычислить интеграл

arctg 2 x

dx .

1 x2

Делаем замену

arctgx t ,

тогда

dt .

1 x2

Следовательно,

arctg 2 x

= t2dt

arctg3 x

C .

1 x2

Вычислить интеграл

xsin 5x dx .

Воспользуемся формулой интегрирования по частям:

udv uv vdu .

x sin(5x)dx

u x

dv sin(5x)dx

cos(5x)dx

du dx

x cos(5x)

cos(5x)

x cos(5x)

sin(5x) C .

5.Вычислить интеграл ln 2x dx .

ln 2x dx =	u ln(2x)			dv dx			xln(2x) x		1	dx xln(2x) x C .
	u ln(2x)			dv dx
	1
	1
	du		dx	v x					x
	du	x	dx	v x					x
						5x 3
6. Вычислить интеграл								dx .
6. Вычислить интеграл					3x2		3x 10	dx .

																											35
																																5		2x 1				11
						5x 3								1				5x 3									1							2x 1
						5x 3								1				5x 3									1				2						2
										dx =														dx							2						2		dx =
	3x2 3x 10									dx =				3		x2 x							10				3							x2 x			10		dx =
																x2 x																		x2 x
																				3																	3
		1			5				2x 1								1 11									dx
													dx
		3				2		x2 x				10					3		2							1 2				37
								x2 x																		1 2				37
									3													x
																						x							12
																										2			12
																									x		1
			5	ln			x2		x		10				11		1			arctg					x		2		C .
			5								10				11		1										2


		6							3					6			37								37

																	12								12

																									(x)
Воспользовались правилом																							(x) dx					ln							(x)	C и табличным
интегралом 9).																							(x) dx
интегралом 9).
7.					Вычислить интеграл																		7x 15										dx .

																					x3 2x2						3x

а) Знаменатель подынтегральной функции разложим на множители: x3 2x2 3x x x2 2x 3 x x 1 x 3 .

б) подынтегральную функцию представим в виде суммы простейших дробей:

	7x 15	A	B	C	.
	x3 2x2 3x		x 3		.
	x3 2x2 3x	x	x 3	x 1
Тогда

7x 15

x 3

x 1

x3 2x2 3x

x x 3 x 1

Следовательно,

7x 15 A x 3 x 1 Bx x 1 Cx x 3 .

Определим постоянные А, В и С.

Если

x 0 ,

то

15 3A

A 5 ;

если

x 3 ,

то

36 12B

B 3;

если

x 1,

то

8 4C

C 2 .

Тогда

7x 15

dx =

x3 2x2 3x

5ln

3ln

x 3

2ln

x 1

C .

x 3

x 1

Задача № 2. Вычислить указанные определѐнные интегралы.

2dx

1.1 7 3x 3 .

Пользуясь правилом								f kx b dx										1	F		kx b C ,
Пользуясь правилом								f kx b dx											F		kx b C ,
																		k
табличным интегралом 1) и формулой Ньютона-Лейбница, получаем:
2	dx			2								1		7 3x								2	2					1			2
2				2																		2	2								2
					= 7 3x 3 dx
	7 3x			3	= 7 3x 3 dx							3					2										7 3x			2
1	7 3x			1								3					2							6			7 3x
				1						1													1								1
																							1								1
															1					1				1			1		5
																										1				.
		6 7		3 2		2		6 7 3 1					2							4	2					1				.
		6 7		3 2				6 7 3 1							6 6					4				6			16		32
	4
2.	x cos 2x dx .						Интегрируя по частям, получаем:
	0
					b					b
					b					b
					udv uv				ba vdu


					a					a
					a					a
4 x cos 2x dx =				u x			dv cos 2xdx							=		x		sin 2x								4	1	4 sin 2xdx
4 x cos 2x dx =				u x			dv cos 2xdx							=				sin 2x								4		4 sin 2xdx
0										1					2										0		2	0
0			du dx				v				sin 2x														0			0

										2
										2


	4										1
=	4	sin			2				0			cos 2x
=		sin			2				0			cos 2x
	2					4					4
			1	0			1	1		2 .
				0				1		2 .
	8		4			4					8


4		sin		1	cos		1	cos 0
	8		2	4		2	4
0

															37
	e			3 x dx
3.			ln	3 x dx						.	Пользуясь формулой замены переменной в определѐнном
3.										.	Пользуясь формулой замены переменной в определѐнном
	1			x
	1
интеграле и учитывая, что ln1 0															и ln e 1,получаем:
	e											ln x t		1		t4	1


		ln3		x dx					=			dx		= t3dt					1		0	1	.
									=			dx	dt	= t3dt									.
	1			x										0	4		0	4		4		4
				x								x						4		4		4


	12						x
			e4					dx =
4.			e4				3	dx =
	9
3 e4					x	12			3 e4 4 e4 3 3 e0 e1											3 1 e 3 e 1 .
					x	12

					3
						9
						9
	При вычислении интеграла воспользовались 3-им правилом
интегрирования и табличным интегралом 4).

Задача № 3. Вычислить площадь фигуры, ограниченной линиями:

y x2 3x 5;

y x 2.

Найдѐм абсциссы точек пересечения графиков, заданных функций. Для этого объединим уравнения в систему

y x2 3x 5,y x 2.

Решая полученную систему уравнений, получаем:

x1 3;

x2 1.

Рис.1.

После построения графиков заданных функций получим фигуру (рис.1),

ограниченную прямой y x 2 и параболой y x2 3x 5.

Площадь фигуры, изображѐнной на рис.1, вычисляется по формуле:

										b
							S f2 (x) f1(x) dx ,
										a
где		f	2		(x) x 2,	f (x) x2		3x 5, следовательно,
			2			1
	1							1							3				1
																			1

S			x 2 x2 3x 5 dx x2 2x 3 dx											x		x2	3x
S			x 2 x2 3x 5 dx x2 2x 3 dx													x2	3x
	3							3					3						3
	3					( 3)3		3											3
		1				( 3)3			2		1							2
				1 3			( 3)			3 ( 3)		2	9 9				9 10			.
				1 3			( 3)			3 ( 3)		2	9 9				9 10			.
		3				3					3							3

Задача № 5. Вычислить объѐм тела, полученного при вращении вокруг оси Ox фигуры, ограниченной линиями:

2	2
x		y	1,	x 6.
2		2
3	2

Первое уравнение задаѐт гиперболу, а уравнение x 6 задаѐт вертикальную прямую. После их построения, получаем фигуру, ограниченную гиперболой и вертикальной прямой.

Рис.2.

Пользуясь формулой для вычисления объѐма тела вращения

VOx f 2 (x) dx ,

находим объѐм тела (рис.2), образованного вращением нашей фигуры вокруг

оси Ox :
	6	4		2			4	x3		6	4	63
	6	4		2			4	x3		6	4	63
VOx	3		x		4	dx			4x				4 6
VOx			x		4	dx			4x				4 6
		9					9	3		3	9	3
										3

		40
	3
4	3	4 3 8 8 16 (куб. ед.)
9	3	4 3 8 8 16 (куб. ед.)
9	3

6
	4 9 x2 dx,						n 8.
	2
	Разобьѐм отрезок интегрирования												[–2;6]					на 8		равных частей с шагом
h	6 ( 2)		1	точками x 2,						x		1,				x		0,		x 1,		x	2,	x 3,
h			1	точками x 2,						x		1,				x		0,		x 1,		x	2,	x 3,
8							0			1					2					3	4			5
8
x6 4,		x7 5,			x8 6 .

		Вычислим					значения		функции							y 4 9 x2					в		этих	точках:

yi y(xi ), i 0;8.							Запишем результаты вычислений в таблицу:

i		0		1				2	3				4					5		6			7	8

xi		-2		-1				0	1				2					3		4			5	6

yi		1,899		1,778				1,732	1,778			1,899					2,060			2,236		2,415		2,590

	Запишем формулы приближѐнного вычисления интеграла для случая
разбиения отрезка интегрирования на 8 частей.
		Формулы прямоугольников:
								b
								y(x) dx h y0					y1		y2				... y7 ,
								a
								b
								y(x) dx h y1					y2		y3				... y8 .
								a
	Формула трапеций:
						b			y		y
									y		y
						y(x) dx h				0			8	y1			y2 ... y7					.
						y(x) dx h					2			y1			y2 ... y7					.
						a					2
						a

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.20211.67 Mб24775.pdf
#
08.01.20211.67 Mб04776.pdf
#
08.01.20211.69 Mб14778.pdf
#
08.01.2021202.51 Кб0478.pdf
#
08.01.20211.7 Mб34780.pdf
#
08.01.20211.71 Mб24781.pdf
#
08.01.20211.71 Mб34782.pdf
#
08.01.20211.71 Mб14783.pdf
#
08.01.20211.72 Mб24784.pdf
#
08.01.20211.72 Mб14785.pdf
#
08.01.20211.72 Mб14786.pdf