
4681
.pdfФедеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Воронежская государственная лесотехническая академия»
МАТЕМАТИКА
ЭЛЕМЕНТЫ ФУНКЦИОНАЛЬНОГО АНАЛИЗА
Методические указания для самостоятельной работы студентов специальности
190601 – Автомобили и автомобильное хозяйство
Воронеж 2010
2
УДК 517.5(075.8)
Котко, Л. А. Математика. Элементы функционального анализа [Текст] : методические указания для самостоятельной работы студентов специальности 190601 – Автомобили и автомобильное хозяйство / Л. А. Котко, С. В. Писарева ; Фед. агентство по образованию, ГОУ ВПО «ВГЛТА». – Воронеж, 2010. – 24 с.
Печатается по решению учебно-методического совета ГОУ ВПО «ВГЛТА» (протокол № 8 от 23 апреля 2010 г.)
Рецензент канд. физ.-мат. наук, доц. кафедры цифровых технологий ВГУ С.А. Скляднев
3
1.МНОЖЕСТВА
1.1Множества
Множества, как правило, обозначают прописными буквами некоторого алфавита A, B, C, N. R… Элементы множества обычно обозначают строчными буквами a, p, e, x, t… Знак  обозначает принадлежность;
обозначает принадлежность; 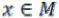
читается «элемент x принадлежит множеству M»; 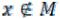 читается «элемент x
читается «элемент x
не принадлежит множеству M».
Буквами N, Z, Q, R обозначают, как правило, множества натуральных, целых, рациональных и действительных чисел соответственно.
Перечислим некоторые, наиболее употребляемые, способы задания множеств:
а) множество может быть задано путем перечисления всех его элементов; например, множество всех цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; множество лиц, присутствующих в комнате {Коля, Володя, Ира, Лена, Оля}; множество всех трехзначных чисел в двоичной системе исчисления {100, 101, 110, 111} и т.п.
b) Множество M может быть задано путем формулирования некоторого
характеристического |
свойства |
P(x), которым обладают элементы множества |
|||
(и только они одни): |
|
или |
. |
|
|
Например, |
множество |
Е |
корней |
уравнения |
, |
где |
|
|
можно составить следующим образом: |
||
Е={x| |
}. |
|
|
|
Множество А точек отрезка [0, 1] задается так: |
A={x: 0 |
}. |
||
c) Множество M может быть задано путем определения его элементов по |
||||
уже известному множеству T. |
|
|
|
|
Например, |
считая |
заданным |
множество |
целых |
чисел |
|
, определим множество |
степеней |
|
числа 2: |
|
|
. |
|
4
Пустым называется множество, не содержащее никаких элементов. Оно обозначается символом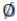 и содержится в любом множестве.
и содержится в любом множестве.
Множества A и B называются равными, если они состоят из одних и тех же элементов.
Если каждый элемент множества A является элементом множества B, то говорят, что множество A содержится в множестве B (пишут 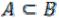 ) или, что то же, множество B содержит множество A (пишут
) или, что то же, множество B содержит множество A (пишут 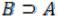 ). В этих случаях говорят, что множество A является подмножеством множества B.
). В этих случаях говорят, что множество A является подмножеством множества B.
1.2 Операции над множествами
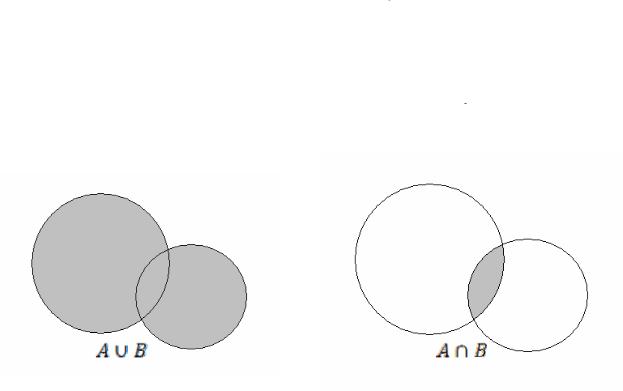
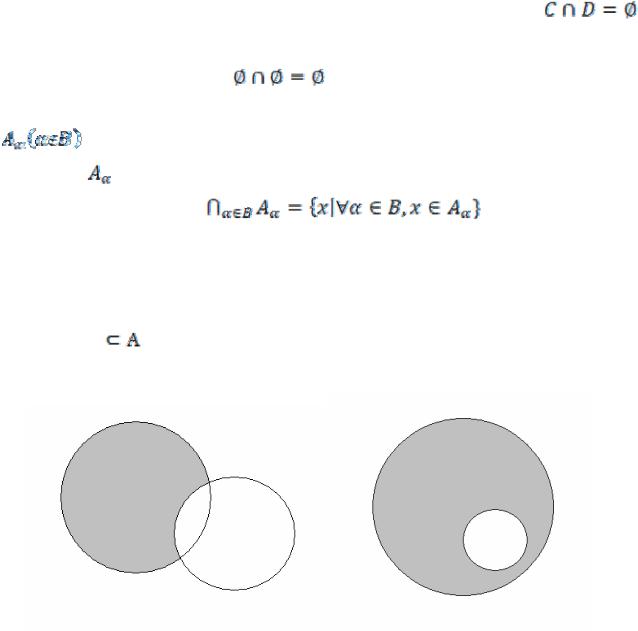
Пусть А и В – произвольные множества; их суммой или объединением 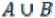 называют множество, состоящее из всех элементов, принадлежащих
называют множество, состоящее из всех элементов, принадлежащих
хотя бы одному из множеств А и В (см. рис. 1).
Аналогично определяется объединение любого (конечного или бесконечного) числа множеств. Пусть 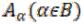 – произвольные множества.
– произвольные множества.
Объединением множеств  называется множество элементов, каждый из которых принадлежит хотя бы одному из множеств
называется множество элементов, каждый из которых принадлежит хотя бы одному из множеств 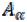 , или
, или
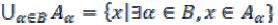 .
.
Очевидно, что для любого А выполняется .
.
A A
B B
Рис. 1 |
Рис. 2 |
5
Пересечением 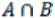 множеств А и В называется множество, состоящее
множеств А и В называется множество, состоящее
из всех элементов, принадлежащих как А, так и В (см. рис. 2).
Например, пересечение множества всех четных чисел и множества всех чисел, делящихся без остатка на три, состоит из всех целых чисел, делящихся
без остатка на шесть. |
|
|
|
Если множества С и D не имеют общих элементов, то |
. |
||
В этом случае множества С и D называются непересекающимися. |
|
||
Полезно отметить, что |
. |
|
|
Пересечением любого (конечного или бесконечного) числа множеств |
|||
|
называется множество |
элементов, принадлежащих каждому |
из |
множеств |
, или |
|
|
|
|
. |
|
Разностью множеств А и В (обозначается А\В) называют множество, |
|
||
состоящее из тех элементов множества А, которые не принадлежат множеству В (см. рис. 3). Ясно, что А\А= .
.
Если В , то А\В называют дополнением множества В до множества |
|
А (см. рис. 4). |
|
А |
А |
|
В |
|
В |
А\В |
|
|
А\В |
Рис. 3 |
Рис. 4 |
В случае, когда рассматриваются различные подмножества множества А |
|
(и только они одни), дополнение множества В до множества А называют просто дополнением.

6
Очевидно, что для любого множества А выполняется А А. Принято также считать, по определению, что пустое множество является подмножеством каждого множества:
А. Принято также считать, по определению, что пустое множество является подмножеством каждого множества: 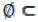 А. Для любого множества А само А и пустое множество называются его несобственными подмножествами. Если же А
А. Для любого множества А само А и пустое множество называются его несобственными подмножествами. Если же А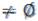 ,
, 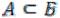 и существует элемент x
и существует элемент x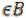 такой, что x не принадлежит А, то А называется собственным подмножеством множества В.
такой, что x не принадлежит А, то А называется собственным подмножеством множества В.
Пример 1. Даны множества А, В и С. С помощью операций объединения и пересечения записать множество, состоящее из элементов, принадлежащих:
1) всем трем множествам; 2) хотя бы одному множеству; 3) по крайней мере двум этим множествам.
Решение. 1) (А
 В)
В) 

 С;
С;
2)(А

 В)
В) 
 С;
С;
3)(А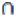 В)
В) 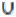 (С
(С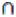 В)
В) 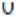 (А
(А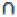 С).
С).
Пример 2. Найти А

 В, А
В, А
 В, А\В, В\А, если А={-4, -3, -2, -1, 0, 1}, B={-1, 0, 1, 2, 3}.
В, А\В, В\А, если А={-4, -3, -2, -1, 0, 1}, B={-1, 0, 1, 2, 3}.
Решение. А
 В={-4, -3, -2, -1, 0, 1, 2, 3}, А
В={-4, -3, -2, -1, 0, 1, 2, 3}, А
 В={-1, 0, 1}, А\В={-4, -3, -2}, В\А={2, 3}.
В={-1, 0, 1}, А\В={-4, -3, -2}, В\А={2, 3}.
1.3 Эквивалентные множества
Говорят, что между множествами А и В установлено взаимно однозначное соответствие, если каждому элементу множества А сопоставлен один и только один элемент множества В так, что различным элементам множества А сопоставлены различные элементы множества В и каждый элемент множества В оказывается сопоставленным некоторому элементу множества А.
Множества, между которыми установлено взаимно однозначное соответствие, называют эквивалентными.
Если множества А и В эквивалентны, то пишут А В.

7
Если А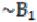 ,
,  и В не эквивалентно А, то говорят, что множество
и В не эквивалентно А, то говорят, что множество
А имеет меньшую мощность, чем множество В.
Множество А называется конечным, если существует такое число n N,
N,
что А {1, 2, 3,…,n}.
В этом случае говорят, что множество А содержит n элементов или что множество А имеет мощность n.
Мощность пустого множества принимается равной нулю. Множество, не являющееся конечным, называется бесконечным. Множество А называется счетным, если А

 N .
N .
Множество называется несчетным, если оно имеет мощность, большую, чем мощность множества N.
Теоремы Кантора.
1.Множество всех рациональных чисел счетно.
2.Множество всех действительных чисел несчетно.
|
Множество А называется множеством мощности |
континуума, |
если |
||||
А . |
|
|
|
|
|
|
|
|
1.4 Бинарные отношения |
|
|
|
|
|
|
|
Прямым |
произведением |
двух множеств |
A={ |
|
|
} и |
B={ |
|
} называется |
множество A |
упорядоченных |
пар |
вида |
|
( |
), где |
|
. |
|
|
|
|
|
Прямым |
произведением |
k множеств |
|
|
называется |
|
множество |
|
упорядоченных |
наборов |
( |
|
) |
|
длины k, где |
|
. |
|
|
|
|
|
|
Эти определения кратко можно записать так: |
|
|
|
|
||
|
A |
|
|
|
|
|
|
.
Пример 1. Перечислите элементы множеств A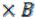 , B
, B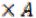 :
:
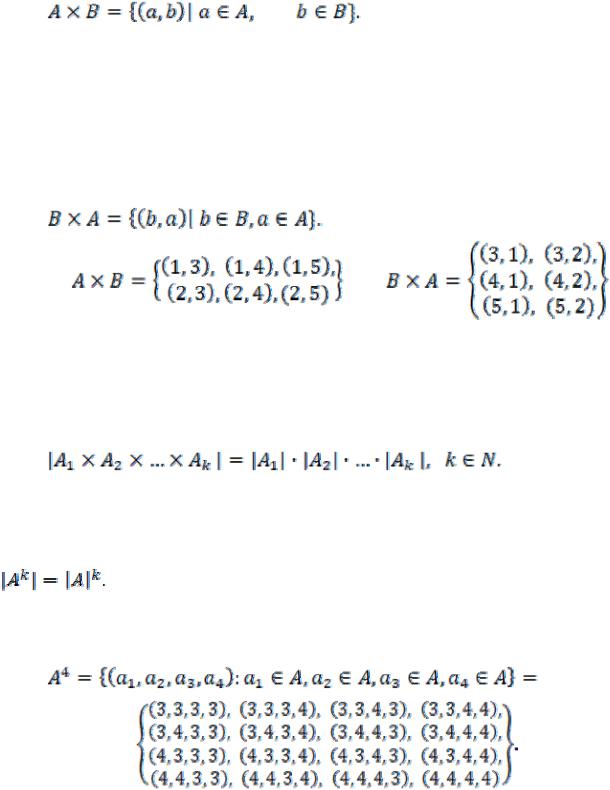
8
1)A={1, 2}, B={3, 4, 5};
2)A= , B={1, 2, 3, 4}.
, B={1, 2, 3, 4}.
Решение. По определению
Порядок построения данного множества будет следующий: вначале перечислим все пары, первый элемент которых равен первому элементу множества А, а второй берется из множества В в том порядке, в котором они записаны в множестве В, затем аналогично берем второй элемент из А и составляем пары со всеми элементами из В и т.д.
Аналогичен и метод построения множества
1) |
, |
. |
2)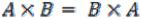 =
=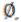 поскольку множество А пусто и мы не можем
поскольку множество А пусто и мы не можем
составить ни одной пары.
Теорема 1. Мощность прямого произведения конечного числа конечных множеств равна произведению мощностей этих множеств.
Множество 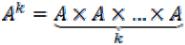 называется k-ой степенью множества A. Из теоремы о мощности прямого произведения следует:
называется k-ой степенью множества A. Из теоремы о мощности прямого произведения следует:
Пример 2. Пусть A={3, 4}. Перечислите элементы множества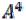 . Решение. По определению
. Решение. По определению
=
Пример 3. Пусть E={0, 1}. Найти мощность множества

|
|
|
9 |
|
|
|
|
|
Решение. |
|
|
|
|
, |
откуда |
следует |
, т.е. мощность множества всех наборов длины n из |
||||||
нулей и единиц равна |
. |
|
|
|
|
|
|
|
Подмножество |
множества |
|
|
называется n |
- местным |
|
отношением на множестве A. |
|
|
|
|
|
||
|
Говорят, что элементы |
|
находятся в отношении |
, если |
|||
|
|
. |
|
|
|
|
|
|
Одноместное отношение – |
это |
просто |
подмножество |
множества |
||
A ( |
) , Такие |
отношения |
называют |
свойствами или |
признаками, |
||
например, свойство четности чисел, признак делимости на три и т.д. |
|
||||||
|
Наиболее часто встречающимися |
являются двуместные или бинарные |
|||||
отношения. Ниже мы будем рассматривать только бинарные отношения. Если
a и b находятся в отношении , то пишут |
или a . |
Примерами отношений на множестве вещественных чисел являются |
|
отношения: « », « », « > », « < », |
« = ». На множестве натуральных |
чисел рассмотрим отношения: а) иметь один и тот же остаток от деления на пять; 2) иметь общий делитель, отличный от единицы. На множестве плоских
прямых |
отметим |
отношения |
параллельности, |
перпендикулярности, |
|||||
симметричности относительно начала координат и др. |
|
|
|||||||
Областью |
определения |
отношения |
на множестве A называется |
||||||
множество тех |
|
|
, для которых существует |
такое |
, что |
. |
|||
Областью значений отношения |
на множестве A называется множество |
||||||||
тех значений |
|
|
, для которых существует такое |
, что |
. |
||||
Поскольку |
отношения |
на множестве |
являются подмножествами |
||||||
множества |
|
, для них можно определить те же операции, что и для множеств: |
|||||||
объединение, |
пересечение, дополнение, разность. Так |
отношение « |
» на |
||||||
множестве натуральных чисел является объединением отношений « < » и « = ». Отношение « > » является дополнением отношения « 

 », а отношение
», а отношение

|
10 |
|
равенства « = » является пересечением отношений « |
» и « » на множестве |
|
действительных чисел. |
|
|
Отношение |
на множестве A называется |
рефлексивным, если |
для |
, и антирефлексивным в противоположном случае: |
|
для |
. |
|
Примерами рефлексивных отношений являются отношения « 

 », « = » и «
», « = » и « 

 » на произвольном числовом множестве.
» на произвольном числовом множестве.
Отношения |
« x < y », «быть сыном», «быть старше» являются |
|||
примерами антирефлексивных отношений. |
|
|
||
Отношение |
на множестве |
A называется симметричным, если из |
||
следует |
. |
Отношение |
называется |
|
антисимметричным, еслииз |
и |
|
следует x=y. |
|
Отношения «жить в одном городе», «иметь общий делитель, отличный от единицы» на множестве целых чисел, «быть симметричным относительно оси» на множестве точек плоскости являются примерами симметричных отношений.
Отношения « », « |
» на |
являются антисимметричными. |
|
|
Отношение |
на множестве A называется транзитивным, если для |
|||
любых |
из |
, |
следует |
. |
Отношения « < », « 

 », « = » на множестве действительных чисел, отношение параллельности прямых, отношение «быть соседом» являются транзитивными. Отношение перпендикулярности прямых, отношение «иметь общий делитель, отличный от единицы» на множестве натуральных чисел свойством транзитивности не обладают.
», « = » на множестве действительных чисел, отношение параллельности прямых, отношение «быть соседом» являются транзитивными. Отношение перпендикулярности прямых, отношение «иметь общий делитель, отличный от единицы» на множестве натуральных чисел свойством транзитивности не обладают.
Отношение называется отношением эквивалентности (или просто эквивалентностью), если оно рефлексивно, симметрично и транзитивно.
Пример 4. Для бинарного отношения выясните, какими свойствами (рефлексивность, симметричность, антисимметричность, транзитивность) оно обладает и какими не обладает.
1) 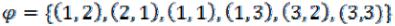 на множестве
на множестве
А={1, 2, 3};
