
4591
.pdf1
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный лесотехнический университет им. Г.Ф. Морозова»
В.И. Посметьев, М.А. Латышева
ДИАГНОСТИКА ТРАНСПОРТНЫХ СРЕДСТВ
методические указания к практическим занятиям для студентов по направлению подготовки 23.04.03 – Эксплуатация транс-
портно-технологических машин и комплексов
Воронеж 2016
2
Посметьев, В. И. Диагностика транспортных средств[Текст] :мето-
дические указания к практическим занятиям для студентов по направлению подготовки 23.04.03 – Эксплуатация транспортно-технологических машин и комплексов / В. И. Посметьев, М. А. Латышева ; М-во образования и науки РФ, ФБОУ ВО «ВГЛТУ». – Воронеж, 2016. – 64 с.
3
ОГЛАВЛЕНИЕ
ОСНОВНЫЕ ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ОТЧЕТА……………….. 4
1 Практическое задание № 1 Контрольные испытания………….………… 5
2 Практическое задание № 2 Надежность нерезервированных невосстанавливаемых систем при внезапных отказах……………………..… 23
3 Практическое задание № 3 Комплексные показатели надежности…….. 34
СПИСОК ЛИТЕРАТУРЫ……………………………………………………… 41
4
ОСНОВНЫЕ ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ОТЧЕТА
Отчет о самостоятельной работе является текстовым документом и выполняется в электронном виде в соответствии с основными требованиями государственных стандартов и соответствующих положений, разработанных в вузе.
Текст отчета оформляется на одной стороне листов бумаги формата А4 (210 297 мм) в один столбец с полями: левое – 25, правое – 10, верхнее и нижнее – 20 мм (рис. 1).
При электронном наборе текста необходимо использовать шрифт "TimesNеwRoman" размером 14 pt, межстрочный интервал – полуторный, выравнивание текста – по ширине, автоматический перенос, отступ в абзаце должен быть одинаковым во всем тексте и равным пяти знакам. Пропуски между буквами в словах и между словами не допускаются. Стиль формул для "MicrosoftEguation": обычный символ – 14, крупный символ – 18, мелкий символ – 12, крупный индекс – 9, мелкий индекс – 7 pt. При оформлении рисунков и таблиц следует использовать более мелкий шрифт 12 pt и межстрочный интервал – одинарный. Рисунки и таблицы отделяются от текста (перед и после) одной строкой. Подчеркивание, а также жирное исполнение заголовков, отдельных слов и т.п. в тексте, таблицах и рисунках с целью их выделения, не разрешается.
Текст контрольной работы выполняют одним из следующих способов: рукописным – с высотой букв и цифр не менее 2,5 мм;с применением компьютера (ГОСТ 2.004-88).
При оформлении текста не допускаются: надрывы, потертости, смятие и загрязнение листов, небрежно выполненные рисунки и таблицы, неаккуратные исправления в тексте и иллюстрационном материале, затрудняющие или делающие невозможным полноценное восприятие представляемого студентом материала самостоятельной работы. Описки (опечатки) и графические неточности, обнаруженные в тексте, допускается исправлять аккуратной подчисткой и нанесением исправлений теми же цветом чернил (пасты), жирностью и толщиной линий. При значительных исправлениях (несколько строк) разрешается аккуратно заклеить ошибочный участок текста полоской бумаги того же качества (набранным текстом) на ней исправленного текста.
Самостоятельной работа должна начинаться с титульного листа, затем содержание, основная часть – решенные задачи и список используемых источников.
Основная часть должна включать номер задачи, ее условие, решение и краткий анализ.
Законченная контрольная работа в обязательном порядке аккуратно сброшюровывается в прозрачную папку-скорошиватель с целью обеспечения надежного хранения.
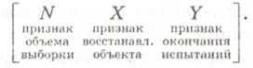
5
Практическое задание № 1 Контрольные испытания
Теоретическая часть
Определительные испытания. Результатом определительных испытаний на надежность являются количественные значения показателей надежности объектов, установленные с заданной точностью и/или достоверностью. Определительные испытания классифицируют по следующим признакам:
1 По характеру оценок показателей надежности различают:
–испытания с целью определения точечных оценок средних значений показателей надежности (средняя наработка до отказа, средний ресурс, среднее время восстановления и пр.); точечной оценкой определяемого показателя в этих испытаниях является среднее арифметическое значение показателя, наблюдаемое при испытаниях выборки из партии однородных объектов;
–испытания с целью определения доверительного интервала возможных значений показателя надежности, который с заданной доверительной вероятностью накрывает математическое ожидание этого показателя.
2 В зависимости от исходных данных различают:
– прямые испытания, основанные на использовании информации об от-
казах объекта;
– испытания, основанные на использовании косвенных признаков отказа (перегрев, уроцни вибрации, шума и пр.).
3 В зависимости от плана испытания делятся на группы, различающиеся правилами, устанавливающими объем выборки, порядок проведения испытаний и критерии их прекращения.
Планы испытаний имеют условные буквенные обозначения следующего вида:
6
Признак объема выборки N— число одновременно испытываемых объ-
ектов.
Признаки восстанавливаемости объекта X расшифровываются сле-
дующим образом:
U–не восстанавливаемые и не заменяемые при испытаниях в случае от-
каза объекты;
R–не восстанавливаемые, но заменяемые в случае . отказа новыми,
идентичными отказавшим экземплярами объекты;
М– восстанавливаемые в случае отказа объекты; г– число отказавших объектов.
Признаки окончания испытаний У расшифровываются следующим об-
разом:
Т– устанавливается время или наработка;
TS–устанавливается суммарная наработка всех объектов;
N–до отказа всех испытываемых объектов; r–устанавливается число отказавших объектов;
(r, Т)– испытание прекращается при числе отказавших объектов r или по достижении наработкиТ каждого работоспособного объекта, независимо от того, какое условие выполнено раньше;
(r, TS)– испытание прекращается при числе отказавших объектов г или по достижении суммарной наработки всех испытываемых объектов
TS,независимо от того, какое условие выполнено раньше;
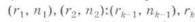 – после rtотказов снимают пх работоспособных объектов и т. д. до достижения rkотказов;
– после rtотказов снимают пх работоспособных объектов и т. д. до достижения rkотказов;
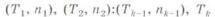 – после достижения наработки Тх снимают пх
– после достижения наработки Тх снимают пх
работоспособных объектов и т. д. до достижения наработки Тк;
z–каждый объект испытывают в течение наработки
 ;t0i– наработка до отказа i-го объекта; ti– наработка до снятия с испытаний работоспособного г-го объекта;
;t0i– наработка до отказа i-го объекта; ti– наработка до снятия с испытаний работоспособного г-го объекта;
S– принятие решения при последовательных контрольных испытаниях.

7
Возможны 17 вариантов различных планов испытаний на надежность:
Для определительных испытаний преимущественно используются пла-
ны
При планировании определительных испытаний определяют объем на-
блюдений и длительность испытаний. При этом задаются показатели досто-
верности результатов (доверительная вероятность) и их точность (предель-
наявеличина относительной погрешности оценки исследуемого показателя надежности).
Методы планирования разработаны для каждого из планов.
ПЛАН [NUN]
Для определения объема наблюдений (объема выборки N)при оценке средних показателей надежности (средняя наработка до отказа, средний ре-
сурс и т. п.) считаются известными следующие исходные данные:
– относительная ошибка 5 оценки соответствующего показателя на-
дежности;
–односторонняя доверительная вероятность оценки ;
–предполагаемый коэффициент вариации 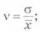 ;
;
–вид закона распределения исследуемой случайной величины (нара-
ботка до отказа, ресурс, срок службы и т. п.).
Относительная ошибка 5 представляет собой меру точности оценки по-
казателя надежности и составляет
где П– оценка показателя надежности; П* – односторонняя доверительная граница показателя надежности (наиболее далеко отстоящая от П).

8
Относительную ошибку выбирают из ряда: 0,05; 0,1;15; 0,2; односто-
роннюю доверительную вероятность – из ряда: 0,8; 0,9; 0,95; 0,99.
Минимальный объем наблюдений Nдля оценки средних показателей надежности определяется следующим образом:
1 Для экспоненциального закона распределения с плотностью 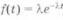 из выражения
из выражения
(1)
где 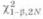 – квантиль 2– распределения с 2Nстепенями свободы, соответст-
– квантиль 2– распределения с 2Nстепенями свободы, соответст-
вующая вероятности 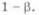 Это трансцендентное уравнение, допускающее только численные ре-
Это трансцендентное уравнение, допускающее только численные ре-
шения, которые табулированы (табл. 1). Прогнозируемая продолжительность испытаний tможет быть определена из выражения
гдеТ– ожидаемая средняя наработка до отказа; Q(t)– минимальная ве-
роятность отказа объекта за время испытаний.
2. Для распределения Вейбулла с плотностью по выражению(1). Реше-
ния уравнения (1) приведены в таблице 1.
Таблица 1– Объем наблюдений для распределения Вейбулла и экспоненциального распределения
|
|
N для плана [NUN]при распределении Вейбулла при раз- |
|
|||||||||
|
|
|
|
личных значениях v |
|
|
|
|
||||
|
|
0,4 |
0,5 |
0,5 |
0,8 |
1 |
1,2 |
1,5 |
1,8 |
2 |
3 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0,05 |
0,80 |
50 |
65 |
100 |
200 |
315 |
500 |
650 |
800 |
1000 |
– |
|
0,90 |
100 |
200 |
250 |
500 |
650 |
1000 |
– |
– |
– |
– |
||
|
||||||||||||
|
0,95 |
150 |
250 |
400 |
650 |
1000 |
– |
– |
– |
– |
– |
|
|
0,99 |
315 |
500 |
800 |
1000 |
– |
– |
– |
– |
– |
– |
|
0,10 |
0,80 |
13 |
25 |
32 |
50 |
100 |
150 |
200 |
250 |
315 |
400 |
|
0,90 |
32 |
50 |
65 |
125 |
200 |
315 |
400 |
500 |
500 |
1000 |
||
|
||||||||||||
|
0,95 |
50 |
80 |
100 |
200 |
400 |
650 |
800 |
800 |
800 |
1000 |
|
|
0,99 |
100 |
150 |
200 |
400 |
650 |
800 |
1000 |
– |
– |
– |
|
0,15 |
0,80 |
6 |
10 |
15 |
25 |
40 |
80 |
80 |
125 |
125 |
200 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|

9
Окончание таблицы 1
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,90 |
15 |
25 |
32 |
65 |
80 |
150 |
200 |
250 |
315 |
500 |
|
|
0,95 |
25 |
10 |
50 |
100 |
150 |
200 |
315 |
100 |
500 |
800 |
|
|
0,99 |
40 |
65 |
100 |
200 |
315 |
500 |
800 |
1000 |
– |
– |
|
|
0,80 |
5 |
8 |
10 |
20 |
25 |
40 |
50 |
65 |
80 |
125 |
|
0,20 |
0,90 |
10 |
15 |
20 |
10 |
50 |
80 |
125 |
150 |
200 |
315 |
|
0,95 |
15 |
25 |
32 |
50 |
100 |
150 |
200 |
250 |
250 |
400 |
||
|
||||||||||||
|
0,99 |
25 |
40 |
65 |
125 |
150 |
250 |
315 |
400 |
500 |
1000 |
3.Для нормального распределения с плотностью
(2)
где t -1 – квантиль распределения Стьюдента cN-1 степенями свободы, соот-
ветствующая вероятности р.
Решения уравнения (2) табулированы, и для определения N можно вос-
пользоваться таблице 2.
Таблица 2 – Объем наблюдений для нормального распределения
|
|
N для плана [NUN] при нормальном распределении при раз- |
||||||
|
|
|
|
личных значениях v |
|
|
||
|
|
0,10 |
0,15 |
|
0,20 |
|
0,25 |
0,30 |
|
0,80 |
4 |
6 |
|
13 |
|
20 |
25 |
0,05 |
0,90 |
8 |
15 |
|
25 |
|
40 |
65 |
0,95 |
13 |
25 |
|
40 |
|
65 |
100 |
|
|
|
|
||||||
|
0,99 |
25 |
50 |
|
100 |
|
150 |
200 |
|
0,80 |
– |
3 |
|
5 |
|
8 |
10 |
0,10 |
0,90 |
3 |
5 |
|
8 |
|
13 |
15 |
0,95 |
5 |
8 |
|
13 |
|
20 |
25 |
|
|
|
|
||||||
|
0,99 |
8 |
15 |
|
25 |
|
32 |
50 |
|
0,80 |
– |
– |
|
3 |
|
4 |
5 |
0,15 |
0,90 |
– |
3 |
|
4 |
|
6 |
8 |
0,95 |
3 |
5 |
|
6 |
|
10 |
13 |
|
|
|
|
||||||
|
0,99 |
5 |
8 |
|
13 |
|
15 |
25 |
|
0,80 |
– |
– |
|
– |
|
– |
3 |
0,20 |
0,90 |
– |
– |
|
4 |
|
5 |
6 |
0,95 |
– |
4 |
|
5 |
|
6 |
8 |
|
|
|
|
||||||
|
0,99 |
4 |
6 |
|
8 |
|
10 |
15 |

10
Следует отметить, что испытания по плану [NUN] требуют значитель-
ного времени (особенно при экспоненциальном законе распределения) и ко-
личества изделий.
Число объектов наблюдений Nдля оценки у-процентных показателей надежности (или вероятности безотказной работы P(t))определяется по вы-
ражению
(3)
где – квантиль распределения Фишера с т и пстепенями свободы, соот-
– квантиль распределения Фишера с т и пстепенями свободы, соот-
ветствующая вероятности;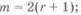
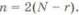
Для нахождения Nнеобходимы следующие исходные данные:
–односторонняя доверительная вероятность ;
–регламентированная вероятность у (или предполагаемое значение P(t));
–установленное число отказов (или предельных состояний) r.
Решения уравнения (3) табулированы и приведены в таблице 3.
Если по результатам наблюдений за Nобъектами получено значение вероятности безотказной работы больше
Таблица 3– Объем наблюдений для плана [NUг]
или |
|
N для плана [NUг] при оценке -процентных показателей надежности при |
||||||||||||
|
|
|
|
различных значениях r |
|
|
|
|
||||||
P(t) |
|
|
|
|
|
|
|
|
||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
8 |
10 |
20 |
10 |
50 |
||
|
|
|||||||||||||
|
0,80 |
8 |
8 |
13 |
20 |
25 |
32 |
40 |
50 |
65 |
125 |
200 |
– |
|
0,80 |
0,90 |
10 |
10 |
15 |
25 |
32 |
40 |
40 |
50 |
65 |
125 |
– |
– |
|
0,95 |
13 |
13 |
20 |
32 |
40 |
40 |
50 |
65 |
80 |
125 |
– |
– |
||
|
||||||||||||||
|
0,99 |
20 |
20 |
25 |
32 |
40 |
50 |
50 |
65 |
80 |
150 |
– |
– |
|
|
0,80 |
15 |
15 |
32 |
40 |
50 |
65 |
80 |
100 |
125 |
200 |
– |
– |
|
0,90 |
0,90 |
20 |
20 |
32 |
50 |
65 |
80 |
80 |
100 |
150 |
200 |
– |
– |
|
0,95 |
20 |
25 |
40 |
50 |
65 |
80 |
100 |
125 |
150 |
– |
– |
– |
||
|
||||||||||||||
|
0,99 |
32 |
32 |
50 |
80 |
80 |
100 |
125 |
125 |
150 |
– |
– |
– |
|
|
0,80 |
32 |
32 |
50 |
80 |
100 |
125 |
150 |
150 |
200 |
– |
– |
– |
|
0,95 |
0,90 |
50 |
50 |
65 |
100 |
100 |
125 |
150 |
200 |
– |
– |
– |
– |
|
0,95 |
50 |
65 |
80 |
125 |
150 |
200 |
– |
– |
– |
– |
– |
– |
||
|
||||||||||||||
|
0,99 |
65 |
65 |
100 |
150 |
150 |
200 |
– |
– |
– |
– |
– |
– |
|
ПЛАН [NUТ]. Число объектов наблюдений Nдля оценки средних пока-
зателей надежности при нормальном распределении может быть определено по таблице 4 при следующих исходных данных:
