8

ментально установлено Гуком, силы, возникающие при упругой деформации, прямо пропорциональны величине этой деформации x и направлены в сторону ее уменьшения:

Fупр = −kx .

Здесь k – жесткость тела – физическая величина, равная силе, при которой деформация x = 1.

Силы трения возникают при соприкосновении поверхностей тел и препятствуют их относительному движению. Различают трение скольжения, трение покоя и трение качения.

Сила трения скольжения вдоль горизонтальной поверхности:

Fтр = μmg ,

где μ – коэффициент трения скольжения, зависящий от рода соприкасающихся поверхностей и качества их обработки, m – масса тела, g – ускорение свобод-

ного падения. Сила трения направлена вдоль поверхности соприкасающихся тел, противоположно силе, вызывающей движение.

Сила трения покоя вычисляется так же, как и сила трения скольжения, но может меняться от нуля до некоторого максимального значения, которое равно силе трения скольжения.

Закон Архимеда. Условие плавания тел

Согласно закону Архимеда на тело, погруженное в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной телом жидкости (газа) и приложенная к центру погруженной части тела:

FA = ρgV ,

где ρ – плотность жидкости; V – объем погруженной части тела; g – ускоре-

ние свободного падения.

Следовательно, на любое тело в жидкости действуют две силы: сила тяжести mg , направленная вертикально вниз, и архимедова сила FA , направлен-

ная вертикально вверх. Если mg < FA , тело тонет; если mg = FA , тело плавает внутри жидкости в состоянии безразличного равновесия; если mg < FA , тело

всплывает на поверхность жидкости до тех пор, пока сила тяжести не уравновесится архимедовой силой, обусловленной погруженной в жидкость частью тела.

Единицы измерения динамических величин (в системе СИ): масса [m] – килограмм (кг); сила [F] = [ma] – (кг·м)/с2 – ньютон (Н).

Импульс тела. Закон сохранения импульса r

Если на тело массой rm в течение времени t действует сила F , скорость движения тела меняется от v0 до v , а ускорение a определяется отношением

ar = v −tv0 ,

то, используя второй закон Ньютона, можно записать

9

Fr =mar =m v −v0 или F t =mvr −mvr0 .

Если на систему тел не действуют внешние силы, то система называется изолированной или замкнутой. Замкнутой можно считать систему, для которой равнодействующая внешних сил равна нулю.

Закон сохранения импульса: векторная сумма импульсов тел замкнутой системы остается постоянной при любых взаимодействиях тел этой системы между собой:

∑n mivri =const .

i=1

Закон сохранения импульса находит широкое практическое применение. Примером может служить реактивное движение, при котором масса тела уменьшается по мере его движения. При старте и дальнейшем полете ракеты продукты сгорания топлива массой mг выбрасываются наружу со скоростью

vrг , при этом, используя закон сохранения импульса (считая систему ракета – газы замкнутой), можно рассчитать скорость ракеты.

Работа силы. Мощность

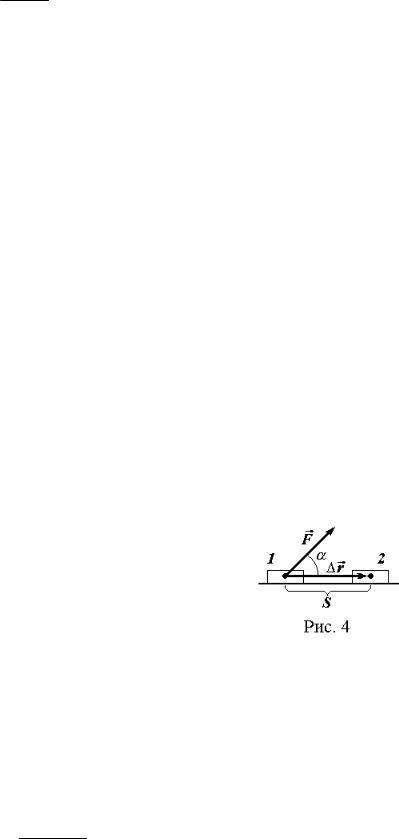
Если под действием силы F тело перемещается из положения 1 в положение 2 как показано на рис. 4, то скалярная физическая величина, численно

Это одна из основных характеристик любой машины, предназначенной для со-

вершения работы. Если движение под действием силы F происходит с постоянной скоростью, то мощность можно выразить в виде произведения:

N = FS cost α = Fv cosα .

Кинетическая энергия. Потенциальная энергия

10

Единая количественная мера всех форм движения материи и взаимопревращений этих форм называется энергией. Механической энергией тела называют физическую величину, характеризующую способность тела совершить работу при изменении своего состояния. В механике различают кинетическую и потенциальную энергию.

Кинетическая энергияr тела массой m определяется работой, которую должна совершить сила F , чтобы покоящемуся телу сообщить скорость v :

= mv2 Ek 2 .

Так же как и скорость, кинетическая энергия тела зависит от выбора системы отсчета.

Потенциальная энергия – это энергия, обусловленная взаимным расположением тел или частей тела друг относительно друга. Например, потенциальная энергия тела массой m , поднятого над Землей на высоту h , определяется соотношением

E p =mgh .

Здесь g – ускорение свободного падения. При этом считается, что потенциаль-

ная энергия тела на поверхности Земли равна нулю.

Потенциальная энергия упруго деформированного тела (например, сжатой пружины) обусловлена изменением взаимного расположения частиц тела (пружины) при деформации:

где k – жесткость тела, x – величина его деформации.

Работа силы тяжести (при падении тела с высоты h ) или силы упругости (восстановление формы пружины после деформации) приводит к уменьшению (убыли) соответствующей потенциальной энергии.

Закон сохранения механической энергии

Сумма кинетической и потенциальной энергий тела составляет его пол-

ную механическую энергию:

E = Ek +E p .

Если в системе тел действуют только силы тяжести или упругости, для нее выполняется закон сохранения механической энергии: полная механиче-

ская энергия такой системы тел остается величиной постоянной при любых взаимодействиях этих тел:

E = Ek +E p =const или Ek1 +E p1 = Ek2 +E p2 .

В отсутствии сил сопротивления в системе могут происходить превращения потенциальной энергии в кинетическую и наоборот, но полная энергия постоянна.

Единицы измерения (в системе СИ):