
4136
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени Г.Ф. МОРОЗОВА»
Кафедра математики
Математика
Методические указания к расчетно-графическим работам для студентов по специальности
09.05.01 – Применение и эксплуатация автоматизированных систем специального назначения
(специализация «Автоматизированные системы обработки информации и управления»)
Воронеж 2018
УДК 512.8
Раецкая, Е. В. Математика [Электронный ресурс]: методические указания к расчетно-графическим работам для студентов по специальности 09.05.01 –
Применение |
и эксплуатация |
автоматизированных систем специального |
назначения |
(специализация |
«Автоматизированные системы обработки |
информации и управления») /Е. В. Раецкая, П.Н. Зюкин, И.В. Сапронов; М- во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2018. – 32 с.
Одобрено решением учебно-методического совета
ФГБОУ ВО «ВГЛТУ» |
(протокол № 6 |
от 23.03.2018 г.) |
Рецензент: д-р физ.-мат. наук, проф. кафедры
математического анализа ВГУ С.П. Зубова
Содержание
Введение……………………………………………………………………..………4
1. Определенный интеграл ……………………………………………..…….…5
1.2 Варианты индивидуальных заданий по теме «Определенный интеграл» ……………………………………………………………………..…...9
2. Ряды…………………………………………………………………………..….17
2.1 Варианты индивидуальных заданий по теме «Ряды» ……..………..23
Библиографический список……………………………………………….…...32
ВВЕДЕНИЕ
Целью изучения дисциплины «Математика» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, обучение основным математическим понятиям и методам математического анализа, аналитической геометрии, линейной алгебры, теории функций комплексного переменного, теории вероятностей и математической статистики, необходимым для анализа и моделирования устройств, процессов и явлений при поиске оптимальных решений практических задач, методам обработки и анализа результатов численных экспериментов.
Для достижения поставленной цели решаются следующие задачи:
–выработка умения решать примеры и задачи для последующего применения математических методов в технических приложениях;
–демонстрация на основе математических понятий и методов сущности научного подхода, специфики математики и ее роли как способа познания мира, общности ее понятий и представлений в решении возникающих проблем.
. В результате освоения дисциплины студент должен:
–знать основные понятия, определения и методы исследования объектов
спомощью теорем и формул различных разделов курса математики;
–решать задачи и примеры по различным разделам высшей математики
сдоведением решения до практического приемлемого результата (формулы, числа, графика, качественного вывода и т.п.), уметь при решении задач выбирать необходимые вычислительные методы и средства (ПЭВМ, таблицы и справочники); самостоятельно изучать научную литературу по математике;
–иметь представление о численных алгоритмах решения математических и прикладных задач его профессиональной области.

1. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ Пример 1.1. Воспользуемся правилом интегрирования
f kx b dx k1 F kx b C ,
табличным интегралом 1) и формулой Ньютона-Лейбница, получим:
2 |
|
dx |
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
7 3x |
2 |
|
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
= |
7 3x 3 dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
7 3x |
3 |
|
|
|
|
|
|
|
|
|
|
6 7 |
3x |
2 |
|
|
|
||||||||||||||||||||||||||||
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
5 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
. |
|
|
|
|
||||||||||
|
6 7 3 2 |
2 |
|
7 3 |
1 |
2 |
|
6 |
|
|
|
4 |
2 |
|
|
|
|
|
32 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
6 |
|
|
|
|
|
|
6 |
|
|
|
6 |
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
Пример 1.2. Воспользуемся методом интегрирования по частям для |
|||||||||||||||||||||||||||||||||||||||||||
вычисления определѐнного интеграла: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
udv uv |
|
ba vdu |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4 x cos 2x dx = |
|
|
u x |
dv cos 2xdx |
|
= |
|
x |
sin 2x |
|
|
4 |
|
1 |
|
|
|
4 sin 2xdx |
|||||||||||||||||||||||||||
|
|
|
|
2 |
|
0 |
2 |
|
|
||||||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|||||||||
|
|
|
|
|
|
du dx |
|
v |
|
sin 2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||
= |
|
|
sin |
2 |
|
|
|
0 |
|
|
|
cos 2x |
||||||
|
|
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|
4 |
|
|
|
4 |
|
|
|
|||
|
|
|
1 |
0 |
1 |
|
1 |
2 . |
|
|||||||||
|
|
|
|
|
||||||||||||||
|
|
8 |
|
4 |
|
|
|
4 |
|
|
|
|
8 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
Пример 1.3. |
|
ln3 x dx |
= |
|||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
0
8 sin 2 14 cos 2 14 cos 0
|
Замена переменной : |
|
|
|
|
|
|||
|
|
|
dx |
|
1 |
t4 |
|
|
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||
= |
ln x t, |
|
dt |
= t3dt |
|
|
|
||
|
|
|
|
|
|
||||
|
|
|
x |
0 |
4 |
|
0 |
||
|
t(1) 0, |
t(e) 1 |
|
||||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
14 40 14 .
Пример 1.4. |
Воспользуемся правилом интегрирования ( ) и |
||||||
табличным интегралом 4): |
|
||||||
12 |
|
|
|
x |
|
||
e4 |
|
|
|
||||
3 dx |
= |
||||||
9 |
|
|
|
|
|
|
|
3 e4 |
x |
|
12 |
3 e4 4 e4 3 |
3 e0 e1 3 1 e 3 e 1 . |
||
|
|||||||
|
|
|
|
||||
3 |
|||||||
|
|
9 |
|
|
|
||
|
|
|
|
||||
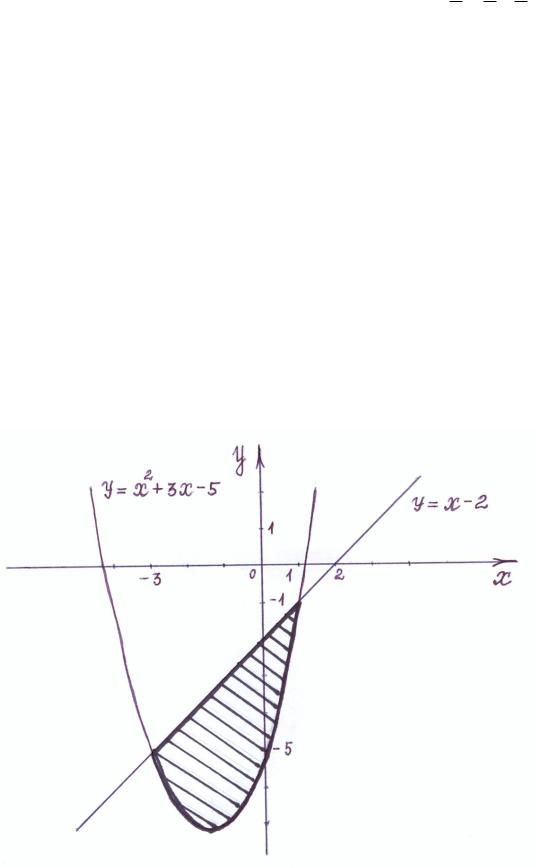
Пример 1.5. Вычислить площадь фигуры, ограниченной линиями:
y x2 3x 5; |
y x 2. |
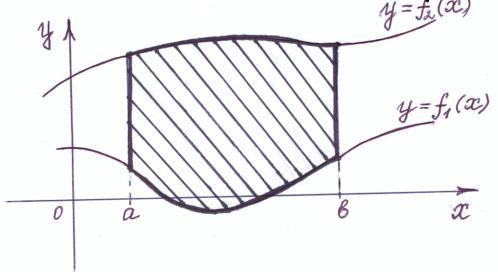
Рис.3
Найдѐм абсциссы точек пересечения графиков, заданных функций. Для этого объединим уравнения в систему
y x2 3x 5,
y x 2.
Решая полученную систему уравнений, получаем:
x1 3; |
x2 1. |
После построения графиков заданных функций получим фигуру (рис.3), ограниченную прямой y x 2 и параболой y x2 3x 5.
Рис.4.
Площадь фигуры, изображѐнной на рис.4, вычисляется по формуле:
|
|
|
|
|
b |
f2 (x) f1(x) dx . |
|
|
|
|
|
|
|
|||
|
|
|
|
S |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
В нашем случае |
f |
2 |
(x) x 2, |
f (x) x2 |
3x 5 , следовательно, |
|
|
|
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
1 |
|
|
|
x3 |
|
|
|
1 |
||
|
|
|
|
|
|
|
|
|
||||||||
S |
x 2 x2 3x 5 dx |
x2 2x 3 dx |
|
|
x2 |
|
3x |
|
|
|||||||
3 |
||||||||||||||||
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
( 3)3 |
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
1 3 |
|
|
|
|
( 3)2 3 ( 3) |
|
|
|
|
2 |
9 9 |
9 10 |
|
(кв. ед.). |
|
|
|
|
|
|
|||||||||||||
|
|
3 |
|
|
|
|
3 |
|
|
|
3 |
|
|
|
3 |
|
||
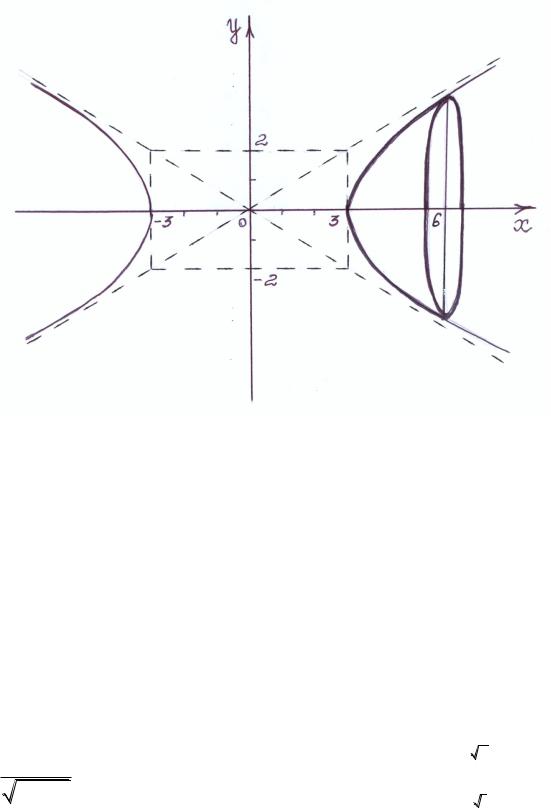
Пример 1.6. Вычислить объѐм тела, полученного при вращении вокруг оси Ox фигуры, ограниченной линиями:
2 |
2 |
|
|
|
x |
|
y |
1, |
x 6. |
2 |
2 |
|||
3 |
2 |
|
|
|
Первое уравнение задаѐт гиперболу, а уравнение x 6 задаѐт вертикальную прямую. После их построения, получаем фигуру, ограниченную гиперболой и вертикальной прямой. Пользуясь формулой для вычисления объѐма тела вращения
b
VOx f 2 (x) dx ,
a
находим объѐм тела (рис.5), образованного вращением нашей фигуры вокруг оси Ox :
|
|
6 |
4 |
|
|
|
4 |
|
x3 |
|
|
6 |
|
4 |
|
63 |
|
|
|
4 |
|
33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
VOx |
|
3 |
|
|
x2 4 |
dx |
|
|
|
4x |
|
|
|
|
|
|
4 6 |
|
|
|
|
|
4 3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
9 |
|
|
|
9 |
|
3 |
|
|
3 |
|
9 |
|
3 |
|
|
|
9 |
|
3 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 8 16 (куб. ед.) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Объѐм тела, образованного вращением вокруг оси Ox фигуры, |
||||||||||||||||||||||||
ограниченной |
|
|
линиями |
y f (x), |
y 0, |
x a, |
|
x b |
(a b) , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
вычисляется |
|
по |
формуле |
VOx f 2 (x) dx . |
|
В |
нашем |
случае |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
y2 |
|
x2 |
1, |
, |
y2 |
|
9 |
x2 |
9, |
a 2, |
b 4, поэтому |
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
9 |
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
4 |
9 |
|
|
|
|
9 |
|
x3 |
|
|
4 |
|
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
VOx |
2 |
|
|
x2 |
9 dx |
|
|
|
9x |
|
|
|
43 |
|
9 4 |
|
|||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
4 |
|
|
|
|
4 3 |
|
|
|
2 |
|
4 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
23 9 2 |
|
12 12 24 . |
|
||||
4 |
|
|
|
|
Рис.5.
1.2 ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ТЕМЕ «ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ»
Задание 1.
Вариант 1.
3dx
1.7 2x ;
1
Вычислить указанные определѐнные интегралы.
|
|
|
|
|
|
|
|
|
2 |
2 |
15 |
|
|
dx |
|
|
|
2. sin3 x cos x dx ; |
3. x ln x dx ; |
4. |
|
|
. |
|||
5 |
x |
2 |
||||||
|
1 |
|
|
|
|
|
||
5 |
|
|
|
|||||
|
|
|
|
|
||||
6 |
|
|
|
|
|
|
|
|
Вариант 2.
|
4 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
e |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
x dx |
|
ln x |
|
|
|
|
|
dx |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
1. |
|
3x 7 dx ; |
2. |
|
; 3. |
|
dx ; |
4. |
|
|
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
sin |
2 |
x |
|
|
x |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
4 x2 |
|||||||||||||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Вариант 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
4 |
|
|
|
dx |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
dx |
|
|
|||||
|
|
|
|
|
|
ex sin(ex ) dx ; |
|
|
|
|
ln x dx ; |
4. |
|
|
|
|||||||||||||||||
1. |
|
|
|
|
|
; 2. |
3. |
|
|
. |
||||||||||||||||||||||
|
|
|
|
|
|
9 x2 |
||||||||||||||||||||||||||
|
|
|
2x 1 |
|
||||||||||||||||||||||||||||
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|||
Вариант 4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2. 2 |
|
|
|
dx |
|
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e3x2 2 dx ; |
||||||||||||||||
|
4x 3 dx ; |
|
|
|
|
|
|
|
|
|
; |
3. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||
|
(arcsin x)3 |
1 x2 |
||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 sin 4x dx .
0
Вариант 5.
2 |
|
dx |
|
|
|
|
|
|
e |
|
|
|
|
|
3 |
|
|
|
|
8 |
dx |
|
|
|
|||
1. |
; |
|
|
2. |
|
|
x3 ln x dx ; |
|
3. |
x2 |
|
x3 3 dx ; |
4. |
|
|
|
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
3x 2 |
|
|
|
|
|
|
cos2 2x |
||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
3 |
x |
|
|
2 |
(5x 5)sin 3x dx ; |
|
5 |
|
|
x5 |
|
|
|
||||||
Вариант 6. |
1. |
|
|
|
|
dx ; |
2. |
|
3. |
|
|
|
|
|
dx ; |
||||||||||||
|
|
|
|
|
7 2x |
6 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 2 |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант 7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
dx |
|
2 ; |
|
2. |
(x 5) ln 5x dx |
; 3. x2 e1 x3 dx ; |
4. |
1 |
|
|
dx 2 . |
||||||||||||||
1. |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
3 |
|
|
|
|
|
|
|
0 1 2x |
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
0 1 9x |
|
|
|
||||||
Вариант 8.
4.
4.
