
4062
.pdf
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ВОРОНЕЖСКАЯ ГОСУДАРСТВЕННАЯ ЛЕСОТЕХНИЧЕСКАЯ АКАДЕМИЯ
М.В. ДРАПАЛЮК
ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
ТЕКСТЫ ЛЕКЦИЙ
Воронеж 2002
2
УДК 621.01 Д 72
Драпалюк М.В. Теория механизмов и машин: Тексты лекций. Воронеж: Воронежс. гос. лесотехн. акад., 2002.- 44 с.
Даны основные определения курса ТММ. Рассмотрен кинематический анализ и синтез механизмов на основе графических и графоаналитических методов. Представлен кинетостатический анализ механизма.
Отдельный раздел посвящен колебаниям в механизмах и различным способам их гашения.
Текст лекций рассчитан на студентов специальности «Лесоинженерное дело», изучающих дисциплину «Теория машин и механизмов»
Печатается по решению редакционно-издательского совета ВГЛТА
Рецензенты:
д-р физ.-мат. наук, проф. кафедры теоретической и прикладной механики Воронежского государственного университета Т.Д. Семыкина,
кафедра прикладной механики ВГАУ
Науч. ред. проф. И.М. Бартенев
|
УДК 621.01 |
С |
Драпалюк М.В. |
С |
Воронежская государственная |
|
лесотехническая академия, 2002 |
3
РАЗДЕЛ 1 ОСНОВНЫЕ ПОНЯТИЯ ТММ. СТРУКТУРНЫЙ АНАЛИЗ И СИНТЕЗ МЕХАНИЗМОВ
Основные определения курса ТММ
Теория машин и механизмов (ТММ) представляет собой науку, состоящую из двух основных частей:
1 Теория механизмов изучает структуру, кинематику и динамику механизмов в связи с их анализом и синтезом.
Анализ – исследование свойств механизмов.
Синтез – проектирование механизмов с заданными свойствами.
2 Теория машин изучает совокупность взаимно связанных механизмов, которая образует машину или систему машин.
Машина – устройство, преобразующее энергию, материалы или информацию в целях облегчения труда человека.
В зависимости от выполняемых функций машины могут быть: энергетическими - преобразуют энергию в механическое движение
(двигатель) или наоборот (генератор); рабочими – преобразуют материалы. Если преобразование материала
заключается только в его перемещении, то такая рабочая машина называется транспортной. Если преобразуется форма или свойства материала, то машина называется технологической.
Контрольно–управляющие машины преобразуют информацию от кон- трольно-измерительных приборов с целью управления энергетической или рабочей машиной.
Математические машины преобразуют информацию, заданную в виде чисел или алгоритмов.
Кибернетические машины имитируют механические, биологические и другие процессы, присущие живой природе, в частности человеку (искусственное сердце, почки).
Машинный агрегат – развитое устройство, состоящее из двигателя, передаточных механизмов, рабочей машины, контрольно-управляющих машин.
Механизм – система тел, предназначенная для преобразования движения одного или нескольких тел в требуемое движение других тел.
Механизм может быть плоским, если точки его звеньев движутся в одной плоскости, либо в параллельных плоскостях. Если это условие не соблюдается, то механизм называется пространственным.
Каждый механизм состоит из отдельных деталей.
Деталь – простейшая часть машины, механизма или прибора выполненная без применения сборочных операций.
Звено – деталь или совокупность деталей, не имеющих относительного движения между собой.
Звенья бывают подвижными и неподвижными. Неподвижное звено в механизме всегда только одно и называется стойкой.
Подвижные звенья в механизме имеют определенные названия в зависимости от характера движения и расположения их в схеме. В рычажных механизмах наиболее часто встречаются следующие звенья:
4
кривошип – звено, совершающее полный оборот вокруг неподвижной
оси;
коромысло – звено, совершающее неполный оборот вокруг неподвижной оси;
шатун – звено, не имеющее общих кинематических пар со стойкой; ползун – звено, входящее в поступательную кинематическую пару с
направляющей; кулиса – подвижная направляющая.
Подвижные звенья соединяются между собой или со стойкой с возможностью движения одного звена относительно другого.
Кинематическая пара – подвижное соединение двух соприкасающихся звеньев.
Кинематические пары делятся на классы. Класс кинематической пары определяется числом условий связи. Под условием связи понимается невозможность какого-либо элементарного движения.
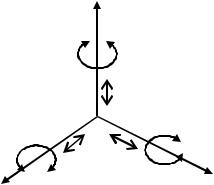
Считается, что любое тело в пространстве может совершать шесть элементарных движений вдоль осей Х;
|
У; Z и вокруг этих осей (рис. 1.1). |
|
|
Если рассматривать кинематиче- |
|
Z |
скую пару, то соединение звеньев |
|
будет накладывать ограничение на |
||
|
||
|
их взаимное перемещение. Сколь- |
|
|
ко элементарных движений стано- |
|
|
вится невозможно, столько усло- |
|
|
вий связи, таков и класс пары |
|
|
(табл. 1.1). |
X
Y
Рис. 1.1 Пространственная система
Элемент звена – совокупность поверхностей, поверхность, линия или точка, по которой звено соприкасается с другим звеном, образуя кинематическую пару.
Высшая кинематическая пара –
такое подвижное соединение, где звенья соприкасаются в точке либо
по линии.
Высшие кинематические образуются при соединении двух зубчатых колес, шара или цилиндра с плоскостью, кулачка с толкателем и т.п.
Низшая кинематическая пара – такое подвижное соединение, где звенья соприкасаются по поверхности.
Низшими кинематическими парами являются соединение ползуна с направляющей (поступательная пара), вращательная пара (цилиндрический шарнир), где звенья соприкасаются по цилиндрической поверхности и т.п.
5
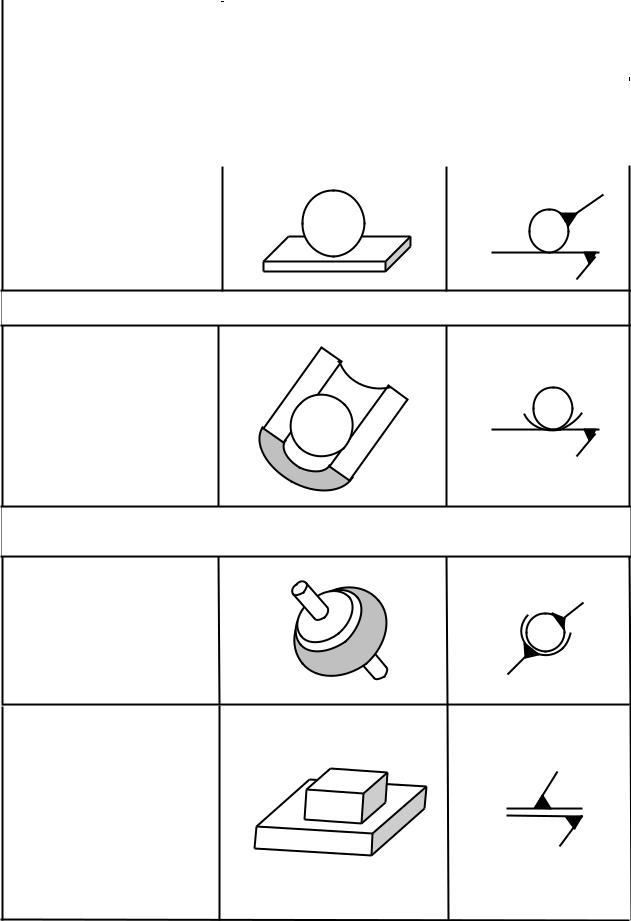
Таблица 1.1 Условное обозначение наиболее распространенных кинематических пар
|
|
|
Обозначение на |
|
Наименование |
Внешний вид |
кинематических |
|
|
|
схемах |
|
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
|
Первый класс |
|
|
|
|
|
Шар - плоскость
Второй класс
Шар - цилиндр
Третий класс
Сферическая
Плоскостная
6
1 |
2 |
3 |
|
|
|
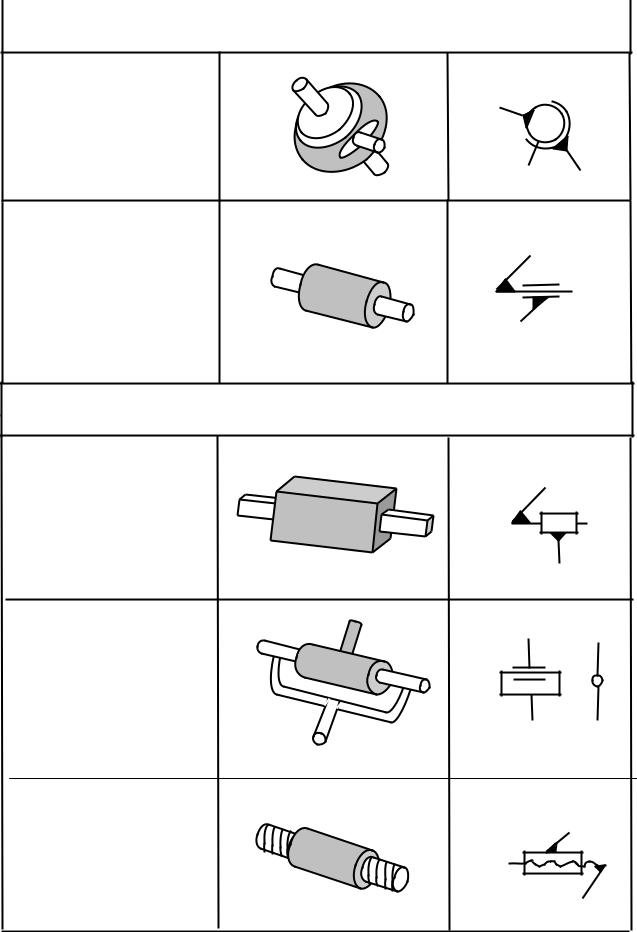
Четвертый класс
Сферическая с пальцем
Цилиндрическая
Пятый класс
Поступательная
Вращательная
Винтовая
7
Структурный анализ механизмов
Кинематическая цепь – это связанная система звеньев, соединенная между собой с образованием кинематических пар.
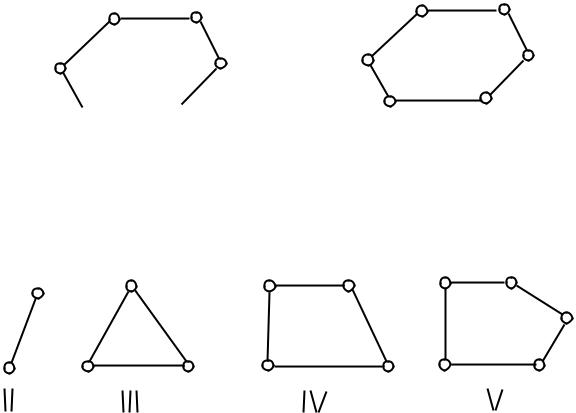
Открытая кинематическая цепь, в которой имеются звенья, входящие только в одну кинематическую пару. В том случае, если подобных звеньев нет, то она называется замкнутой кинематической цепью (рис. 1.2). Кинематическое соединение – кинематическая цепь, конструктивно заменяющая кинематическую пару (подшипник качения, соединение шатуна и поршня через поршневой палец).
Рис. 1.2 Схема открытой и замкнутой кинематической цепи
Одно звено либо система могут образовывать замкнутый контур, который не разбивается на более простые.
Класс замкнутого контура определяется числом кинематических пар, его образующих (рис. 2.2).
Рис. 1.3 Замкнутые контуры различных классов
Одной из важнейших характеристик механизма является число степеней подвижности.
Число степеней подвижности (свободы) W показывает, сколько необходимо задать простых входных движений, чтобы охарактеризовать положение любого звена относительно стойки.
Например, число степеней подвижности W=1 показывает, что движения одного входного (ведущего) звена вполне достаточно, чтобы однозначно определить движение всех остальных звеньев механизма.
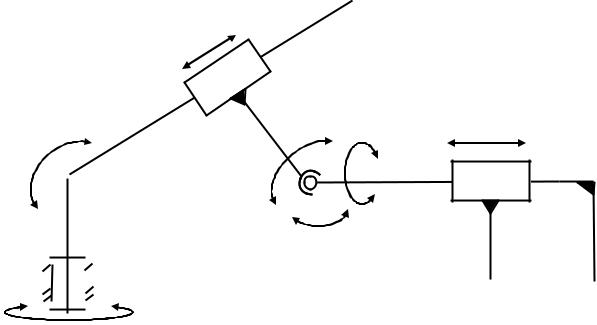
Степень подвижности пространственных механизмов определяется по формуле Сомова-Малышева
8 |
|
W = 6n − 5p5 − 4p4 − 3p3 − 2p2 − p1 , |
(1.1) |
где n – число подвижных звеньев; p5 – число кинематических пар пятого класса; p4 – число кинематических пар четвертого класса и т.п.
Определим число степеней подвижности пространственного механизма (рис. 1.4).
С
2 |
3 |
Е |
|
||
|
|
4 |
 В
В
D
1
5
0 
 А
А
Рис. 1.4 Кинематическая схема пространственного механизма
Данный механизм содержит пять подвижных звеньев: 1; 2; 3; 4; 5, т.е.
n = 5; четыре кинематические пары пятого класса: А, В, С, Е, таким образом р5 = 4; одну кинематическую пару третьего класса – D, т.е. р3 = 1; кинематические пары первого, второго и четвертого класса отсутствуют р1 =0, р2 = 0, р4 = 0. Подставив полученные значения в формулу 1.1, получим
W = 6n−5p5 −4p4 −3p3 −2p2 − p1 = 6 5−5 4−4 0−3 1−2 0−0 = 7.
Число степеней свободы W = 7 говорит о том, что необходимо задать семь входных движений, чтобы определить движение всех звеньев механизма.
Число степеней подвижности плоского механизма определяется по формуле П.Л. Чебышева
W = 3n − 2p5 − p4 или W = 3n − 2 p2 − p1 , |
(1.2) |
где n – количество подвижных звеньев; р5 – количество кинематических пар пятого класса; p4 – количество кинематических пар четвертого класса; р2 – количество низших кинематических пар; р1 – количество высших кинематических пар.
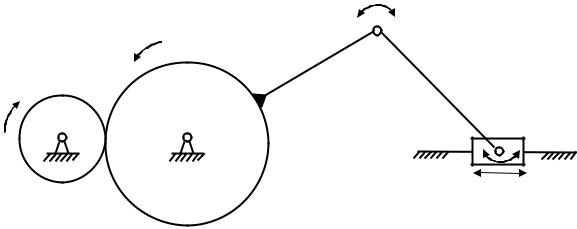
Определим число степеней подвижности плоского механизма (рис. 1.5). Подвижными звеньями данного механизма являются: зубчатые колеса 1; 2, кривошип 3 и ползун 4. К низшим кинематическим парам относятся вра-
щательные кинематические пары А; С; D; Е; F и поступательная кинемати-
9 |
|
|
ческая пара F, так как их звенья соприкасаются |
по |
поверхности. |
Зубчатые звенья 1 и 2, соприкасаясь по линии, образуют высшую кинематическую пару В. Таким образом, механизм содержит четыре подвижных звена n = 4, одну высшую кинематическую пару р1 = 1 и пять низших кинематических р2 = 5. Подставив, полученные значения в формулу 1.2, получим
W = 3 4 − 2 5 −1=1.
|
|
|
D |
|
|
|
3 |
А |
В |
С |
|
|
2 |
||
|
|
||
1 |
|
2 |
|
|
E |
||
|
|
||
|
|
|
|
0 |
|
0 |
0 |
|
|
|
F |
Рис. 1.5 Кинематическая схема плоского механизма
Число степеней подвижности определяет количество элементарных входных движений. Входное движение задает ведущее звено, которое является частью механизма первого класса. Механизм первого класса – ведущее звено, соединенное кинематической парой со стойкой. Таким образом, сколько степеней свободы имеет механизм, столько и механизмов первого класса он должен содержать. При проектировании механизма с заданным количеством степеней свободы необходимо взять столько же механизмов первого класса. Помимо ведущих звеньев механизм может содержать и другие группы звеньев, которые не должны нарушать заданной степени свободы. Такие группы называются группами Ассура.
Группа Ассура – открытая кинематическая цепь, которая при присоединении к механизму не изменяет его числа степеней свободы.
Если группу Ассура присоединить свободными элементами звеньев к стойке, то она станет неподвижной(W=0).
Любой механизм можно представить как совокупность некоторого количества механизмов первого класса и некоторого количества групп Ассура. Для того чтобы выполнялось условие W=0, количество звеньев в группе Ассура должно составлять 2/3 от количества низших кинематических пар:
W = 3n − 2p2 − p1 ;
W=0; p1=0 → n = ⅔ p2
Данное выражение удовлетворяет следующий ряд целых чисел:
n |
2 |
4 |
6 |
8 |
… |
р2 |
3 |
6 |
9 |
12 |
… |

10
Пользуясь данными значениями, можно составить различные группы Ассура (рис. 1.6).
B B

 F
F  B
B 


 E
E
A  C A
C A 
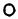 F
F
A C 



 C
C 
 D
D
D 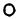 E Рис. 1.6 Примеры групп Ассура
E Рис. 1.6 Примеры групп Ассура
Класс группы Ассура определяется высшим классом замкнутого контура, входящего в его состав.
Класс замкнутого контура определяется количеством кинематических пар, входящих в контур.
Порядок группы Ассура определяется числом свободных элементов, которыми группа Ассура присоединяется к механизму.
Избыточные связи. Лишние степени свободы. Замена высших кинематических пар на низшие
Избыточные (пассивные) связи – звенья и кинематические пары, формально уменьшающие степень подвижности механизма, но фактически не влияющие на его кинематику. При конструировании плоских механизмов избыточные связи часто вводят по конструктивным соображениям для повышения жесткости конструкции, снижения контактных напряжений или для устранения неопределенности их движения в некоторых положениях.
На рис. 1.7 а представлена схема механизма, избыточными связями которого являются звено 1 и кинематические пары А и F. При подсчете числа степеней свободы получим ноль. Фактически число степеней свободы этого механизма – единица. После удаления избыточных связей из механизма (рис.1.7 б) получим W=1.
С |
3 |
D |
В |
2 |
|
|
С |
||
2 |
|
4 |
1 |
3 |
|
|
|
||
В |
|
|
А |
D |
|
|
E |
|
|
А  F 1
F 1
б
а
Рис. 1.7 К определению избыточных связей в механизме
