4038

Например, если rxy = 0,8, то rxy2 = 0,64, т.е. 64 % всех изменений одного признака связано с изменением другого.

Доверительным интервалом статистической оценки истинного значения коэффициента корреляции нормально распределенных случайных величин Х и Y является интервал

Здесь rxy – выборочный коэффициент корреляции, величина t находится по таблице значений функции Лапласа (прил. 1) из условия Ф( t ) = 2 , где –

заданный доверительный уровень.

11. УРАВНЕНИЯ ЛИНЕЙНЫХ СРЕДНЕКВАДРАТИЧЕСКИХ РЕГРЕССИЙ

Уравнением линейной среднеквадратической регрессии величины X

на величину Y называется уравнение

x xâ rxy y yâ .â( X ) â( Y )

Уравнением линейной среднеквадратической регрессии величины Y

на величину X называется уравнение

y yâ rxy x xâ .â( Y ) â( X )

Пример 11.1

23

Найти коэффициент корреляции и составить уравнение линейной регрессии величины Y на величину X .

Составим корреляционную таблицу с условными вариантами:

24

Определяем B (U ) и B (V ) :

B (U ) = 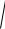uB 2 (uB )2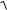 2,872 ( 0,487)2 1,623;

B (V ) = vB 2 (vB )2 2,423 ( 0,885)2 1,281.

i 1

появления пары ( ui ,v j )):

25

7 1 ( 2) 3 ( 3) ( 1) 4 ( 1) ( 1) 5 0 ( 1) 6 2 ( 1) 5 ( 3) 0

3 ( 2) 0 10 0 0 2 1 0 2 ( 2) 1 3 ( 1) 1 3 1 1 5 2 1 67.

Тогда 781 67 ( 0,487) ( 0,885) 0,428 , а значит

Осуществим переход к исходным вариантам:

xB hx uB u0 5 ( 0,487) 35 32,565;

yB hy vB v0 10 ( 0,885) 60 51,15;

B (X ) hx B (U ) 5 1,623 8,115;

B (Y ) hy B (V ) 10 1,281 12,81.

Находим уравнение линейной регрессии величины Y на величину X . Это уравнение имеет вид:

После упрощения получаем уравнение линейной регрессии величины Y на величину X в виде:

y =0,325 x +40,566.

12.ВЫРАВНИВАНИЕ ЭМПИРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ ПО КРИВОЙ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Рассмотрим дискретную случайную величину X , закон распределения которой неизвестен. Пусть произведено n испытаний, в которых величина X

26

приняла n1 раз значение x1 , n2 раз значение x2 , … , nk раз значение xk ,

k

причем ni n . i 1

Эмпирическими частотами называют фактически наблюдаемые частоты ni .

Пусть имеются основания предположить, что изучаемая случайная величина X распределена по некоторому определенному закону. Чтобы проверить, согласуется ли это предположение с данными наблюдений,

найденные теоретически (вычислением). Выравнивающие частоты находят с помощью равенства

дискретного распределения равна произведению числа испытаний на вероятность этого наблюдаемого значения.

В случае непрерывного распределения, вероятности отдельных возможных значений равны нулю. Поэтому весь интервал возможных значений делят на k непересекающихся интервалов и вычисляют вероятности Pi

попадания X в i-й частичный интервал, а затем, как и для дискретного распределения, умножают число испытаний на эти вероятности.

Итак, выравнивающие частоты непрерывного распределения находят по равенству

n n P ,

i i

27

где n – число испытаний; Pi – вероятность попадания X в i-й частичный интервал, вычисленная при допущении, что X имеет предполагаемое распределение.

Если имеются основания предположить, что случайная величина X (генеральная совокупность) распределена нормально, то выравнивающие частоты могут быть найдены по формуле

Замечание 1

1) При использовании таблицы для вычисления значений функции ( õ )

следует учитывать, что эта функция четная, т. е. ( õ ) ( õ ).

2) Чтобы пользоваться таблицей значений функции ( õ ) , достаточно вычислять числа ti с двумя знаками после запятой.

Если эмпирическое распределение задано в виде последовательности интервалов и соответствующих им частот, то для вычисления теоретических частот нормально распределенной случайной величины можно воспользоваться более точными формулами

частичного интервала разбиения, Ô( x) - функция Лапласа, значения которой находятся по таблице прил. 1.

28

Замечание 2

1) При использовании таблицы для вычисления значений функции Ô( x)

Построить полигон частот и нормальную кривую по данному распределению.

Решение.

С целью упрощения вычислений перейдем к условным вариантам

Тогда

xâ uo h uâ 35 5 ( 0,06 ) 34,7 ,

Вычислим выравнивающие частоты (табл. 12.2)

Т а б л и ц а 12.2

Первый и последний столбцы табл. 12.2 дают координаты точек ( õ , n ), i i

по которым строится кривая нормального распределения.

Рис. 12.1 Близость теоретических и эмпирических частот говорит в пользу

предположения о нормальном законе заданного распределения.

На рис. 12.1 построены нормальная (теоретическая) кривая по выравнивающим частотам (они отмечены крестиками) и полигон наблюдаемых частот (они отмечены точками). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений. Для того чтобы более уверенно считать, что данные наблюдений свидетельствуют о нормальном распределении признака, пользуются специальными правилами, которые называют критериями согласия.

13. ПРОВЕРКА ГИПОТЕЗЫ О ЗАКОНЕ РАСПРЕДЕЛЕНИИ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ. КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА

Обычно в практических задачах не встречаются случайные величины, распределения которых точно соответствовали бы теоретическим распределениям. Последние представляют собой математические модели реальных распределений. Подбор таких моделей и анализ их адекватности моделируемым случайным величинам являются одной из основных задач

31

математической статистики. Эта задача в свою очередь сводится к проверке предположений (гипотез) о виде модели распределения и ее параметрах.

Статистической гипотезой (или просто гипотезой) называется любое предположение о генеральной совокупности, проверяемое по выборке.

Нулевой (основной) гипотезой H0 называется предположение, которое выдвигается изначально, пока наблюдения не заставят признать обратное.

Альтернативной (конкурирующей) гипотезой H1 называется гипотеза,

которая противоречит нулевой гипотезе и которую принимают, если отвергнута основная гипотеза.

Процедура сопоставления высказанного предположения (гипотезы) с выборочными данными называется проверкой гипотез.

Задачи статистической проверки гипотез:

относительно некоторой генеральной совокупности высказывается та или иная гипотеза Н;

из этой генеральной совокупности извлекается выборка;

необходимо указать правило, с помощью которого можно было по выборке

ответить на вопрос о том, следует ли отклонить гипотезу Н или принять ее.

Отметим, что статистическими методами гипотезу можно только опровергнуть или не опровергнуть, но не доказать.

Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т. е. могут быть допущены ошибки двух родов.

Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.

Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.

Уровнем значимости называется вероятность совершить ошибку первого рода, т. е. отвергнуть правильную гипотезу. Правило, по которому принимается решение принять или отклонить гипотезу H0 (или

32