3179

2

УДК 517.52(075.4)

Котко Л.А., Чернышов К.И. Ряды [Текст]: методические указания и контрольные задания для студентов 2 курса специальностей 190601 – Автомобили и автомобильное хозяйство, 190702 – Организация и безопасность движения, 150405 – Машины и оборудование лесного комплекса / Л.А. Котко, К.И. Чернышов; Фед. агентство по образованию, Гос. образовательное учреждение высш. проф. Образования, Воронеж. гос. лесотехн. акад. –

Воронеж, 2007. – 40 с.

Печатается по решению редакционно-издательского совета ВГЛТА

Рецензент канд. физ.-мат. наук, доцент кафедры высшей математики и физико-математического моделирования А.П. Дубровская

3

Теория рядов начала создаваться в 17 век, а точное обоснование носила в 19 веке. Эта теория дает возможность изучать функции достаточно широкого класса путем их представления в виде сумм определенного ряда элементарных функций. Разложение функций в ряды применяется в различных разделах математики: при приближенном вычислении значений функции, интегралов (в том чисел неберущихся), при решении дифференциальных уравнений и в других задачах. Замена исследуемой функции соответствующим рядом влечет необходимость исследования поведения этого ряда.

Поскольку имеется большое количество различных признаков, позволяющих исследовать поведение ряда, то возникает необходимость в классификации некоторых из этих признаков. Настоящая разработка поможет пользоваться ими на основании наглядных схем.

Числовой ряд, основные понятия.

Пусть каждому натуральному числу n поставлено в соответствие некоторое действительное число un. Элементом un будем называть пару, состоящую из числа n R.

Числовой последовательностью, или просто последовательностью, называется совокупность элементов un, n N. Элемент un называется n-м членом этой последовательности, а число n - его номером.

Очевидно, что последовательность является частным случаем функции. Именно, последовательность является функцией, определенной на множестве N и принимающей значения в множестве R.

Например, 1, 3, 5, 7,… - последовательность всех нечетных натуральных чисел, un = 2n – 1, n N.

Конечное число a называется пределом последовательности un, если для любого ε > 0 существует такой номер nε , что при всех n > nε , выполняется неравенство un − a <ε.

Не всякая последовательность имеет предел.

Последовательность, не имеющая предела, называется расходящейся. Например, un = n; un =(−1)n−1. Первая из последовательностей сходится к

+ ∞, а вторая не имеет предела.

4

Чтобы сформулировать достаточное условие сходимости последовательности, введем понятия монотонной, а также ограниченной последовательности.

Последовательность un называется ограниченной сверху (снизу), если существует такое число M(m), что un ≤ M (un ≥ m) при всех n N.

Справедлива Теорема 1. Ограниченная сверху (снизу) неубывающая (невозрастающая)

последовательность un сходится.

Числовым рядом называется выражение вида

Числа u1,u2 , ... , un , ... называются членами ряда, n-й член ряда

называется также общим членом ряда.

n-й частичной суммой ряда (1) называется число Sn, равное сумме первых его n членов

Sn = u1 + u2 +... + un .

Тем самым ряду (1) ставится в соответствие последовательность Sn такая,

что

S1 =u1, S2 = u1 + u2 , S3 = u1 + u2 + u3 , ... , Sn = u1 + u2 +... + un , ... .

Ряд (1) называется сходящимся, если последовательность Sn имеет (конечный) предел S. В этом случае S называют суммой ряда и пишут, что

∞

∑un = S.

n=1

Ряд (1) называется расходящимся, если lim Sn не существует.

n→∞

Необходимый признак сходимости ряда.

Если ряд (1) сходится, то lim un =0.

n→∞

Равносильным утверждением является Достаточный признак расходимости ряда.

Алгоритм применения необходимого признака сходимости ряда

5

Ответ: ряд расходится.

Ряды с положительными членами.

Рассмотрим ряд, у которого все члены положительны

n =1

Последовательность Sn частичных сумм этого ряда является возрастающей, так как при всех n = 2, 3, …

Sn = Sn−1 + un,

причем un > 0. Тогда либо последовательность Sn является неограниченной и,

1 имеет конечный предел.

Отсюда и из определений сходимости и расходимости ряда вытекает следующее утверждение:

и ряд расходится, либо последовательность Sn частичных сумм ограничена и ряд сходится.

Замечание. Теорема 2 справедлива и для рядов с неотрицательными членами.

Достаточные признаки сходимости и расходимости ряда с положительными членами.

Даже при условии, что для ряда (2) выполнен необходимый признак сходимости, нельзя решить вопрос о его сходимости или расходимости без дополнительного исследования.

Этот ряд называется рядом Дирихле или обобщенным гармоническим рядом. Известно, что при α ≤1 он расходится, а при α >1 − сходится. В то же время при всех при α > 0 имеем

втором – сходится.

Вывод: необходимый признак сходимости ряда не является достаточным признаком сходимости этого ряда.

Таким образом, для исследования сходимости или расходимости ряда (2) наряду с упомянутым необходимым признаком сходимости (или, что то же, достаточным признаком расходимости) нам требуются и другие, достаточные признаки сходимости или расходимости этого ряда. Из множества таких признаков мы изучим три признака сравнения, признаки Даламбера и Коши, а также интегральный признак Коши.

расходятся одновременно.

Как применять признаки сравнения.

По исследуемому ряду (3) нужно выбрать самим ряд (4) с известным поведением (ряд (4) называется эталонным). В качестве эталонного ряда чаще всего используют один из двух рядов:

а) ряд Дирихле (обобщенный гармонический ряд); б) ряд геометрической прогрессии

∞

∑aqn −1, a ≠ 0,

n =1

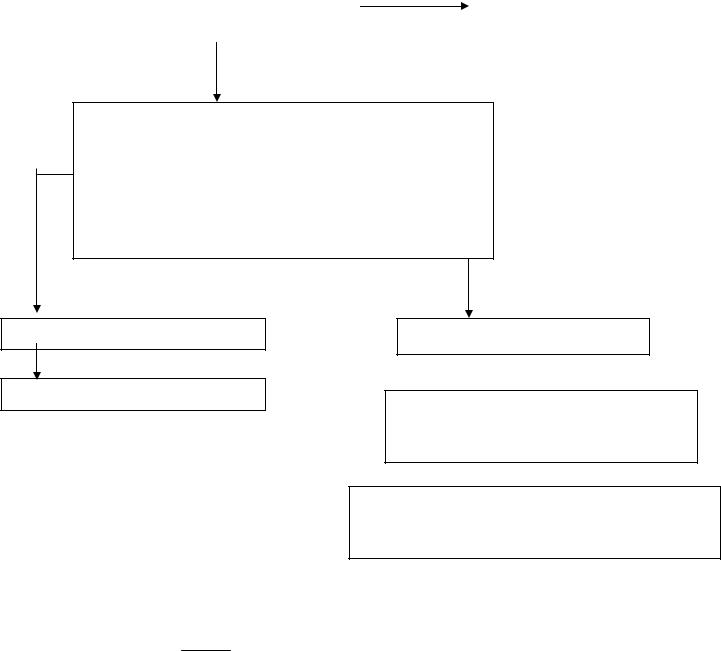
который сходится при q <1 и расходится при q ≥1. Алгоритм применения 1-го признака сравнения

n=1

осуществляется согласно двум критериям: а) известно поведение ряда (4);

б) справедливо неравенство un ≥υn , n ≥ n0

Рекомендация: нужно выбрать либо другой эталонный ряд, либо применить другой признак

рядом, он является рядом Дирихле с α =1, а значит, расходится. Вследствие 2-го признака сравнения исследуемый ряд также расходится.

10

Ответ: ряд расходится.

Алгоритм применения 3-го признака сравнения.

∞

исследуемый ряд ∑u n

n=1