Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежская государственная лесотехническая академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2221

.pdf

Скачиваний:

Добавлен:

08.01.2021

Размер:

365.42 Кб

Скачать

☆

1 / 21 2 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ ЛЕСОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ имени Г.Ф. МОРОЗОВА»

Кафедра математики

Линейная алгебра

Методические указания к расчетно-графическим работам для студентов по направлению подготовки

38.03.01 – Экономика

Воронеж 2018

УДК 512.8

Раецкая, Е. В. Линейная алгебра [Электронный ресурс]: методические указания к расчетно-графическим работам для студентов по направлению подготовки 38.03.01 – Экономика / Е. В. Раецкая, П.Н. Зюкин П.Н., Сапронов ; М-во образования и науки РФ, ФГБОУ ВО «ВГЛТУ». – Воронеж, 2018.

Одобрено решением учебно-методического совета

ФГБОУ ВО «ВГЛТУ»

(протокол № 6

от 23.03.2018 г.)

Рецензент: д-р физ.-мат. наук, проф. кафедры

математического анализа ВГУ С.П. Зубова

Содержание

Введение…………………………………………………………………………....4

1.1 Элементы линейной алгебры ……….………………………………………5

2.1 Варианты индивидуальных заданий по теме «Элементы линейной алгебры»………………………….………………………………………………….9

Библиографический список…………………………………………………...16

ВВЕДЕНИЕ

Целью изучения дисциплины «Линейная алгебра» является воспитание достаточно высокой математической культуры, привитие навыков современных видов математического мышления, обучение основным математическим понятиям и методам линейной алгебры, необходимым для анализа и моделирования устройств, процессов и явлений при поиске оптимальных решений практических задач, методам обработки и анализа результатов численных экспериментов для экономических задач.

Для достижения поставленной цели решаются следующие задачи:

- закрепление теоретического материала и выработка умения решать примеры и задачи для последующего применения математических методов в технических приложениях;

- демонстрация на основе математических понятий и методов сущности научного подхода, специфики математики и ее роли как способа познания мира, общности ее понятий и представлений в решении возникающих проблем.

Для эффективного освоения дисциплины «Линейная алгебра»	у
обучающегося должны быть сформированы следующие представления

-представления о математике как части мировой культуры и о месте математики в современной цивилизации, о способах описания на математическом языке явлений реального мира;

-представления о математических понятиях как о важнейших математических моделях, позволяющих описывать и изучать разные процессы

иявления; понимание возможности аксиоматического построения математических теорий.

Студент по результатам освоения дисциплины «Линейная алгебра» должен владеть методами доказательств и алгоритмов решения; умение их применять, проводить доказательные рассуждения в ходе решения задач;

- основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать на чертежах, моделях и в реальном мире геометрические фигуры; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием.

1.1 ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ

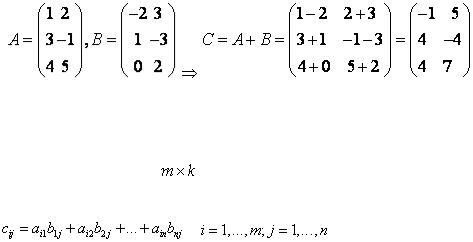
Матрицей А размера m n называется таблица из				m n чисел
a11	a12	...	a1n

a21	a22	...	a2n
A			...
...	...	...	...

	am2	...
am1	am2	...	amn

Часто для краткости пишу A aij . Числа, из которых состоит

матрица, называются элементами матрицы. Индексы у элементов матрицы указывают расположение этого элемента в таблице: первый индекс – номер строки, в которой находится элемент, а второй – номер столбца. Например, элемент a21 находится на пересечении второй строки и первого столбца:

	a	a	...	a
	11	12		1n

	a21	a22	...	a2n
A
A

...		...	...	...
		am2	...
am1		am2	...	amn

Суммой

двух

матриц одинакового размера m n

aij

называют матрицу C

cij

размера m n такую, что

bij

cij

aij

bij ,

i 1,..., m ;

j 1,...n .

Произведением матриц АВ называется матрица

C		cij		размера	, у которой
					,

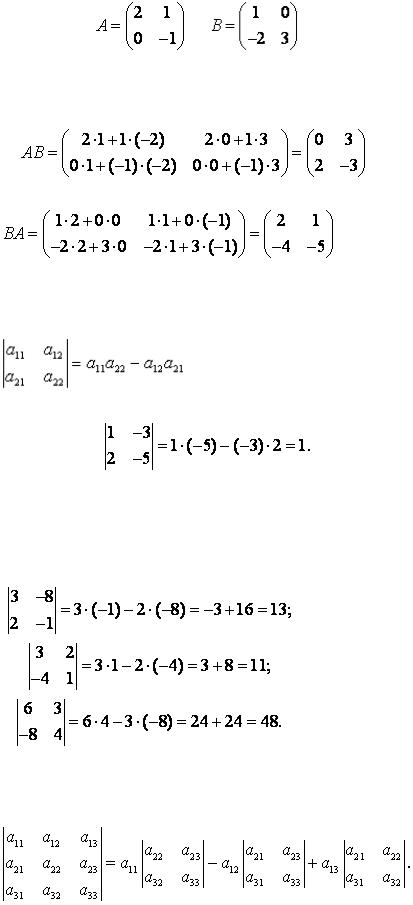
Пусть,

Тогда

Определителем матрицы 2-го порядка называется число

Например,

Найдем определители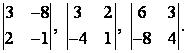

Определителем матрицы 3-го порядка называется число

например,

Mij .

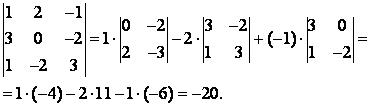
Алгебраическим дополнением Aij элемента определителя называется его минор, если сумма индексов данного элемента i j есть число четное, или число, противоположное минору, если i j нечетно, т.е. Aij ( 1)i j

Обозначим через A матрицу, составленную из алгебраических дополнений матрицы A .

Квадратная матрица B называется обратной к квадратной матрице A того же порядка, если AB BA E . При этом B обозначается A 1 .

Для существования обратной матрицы необходимо и достаточно, чтобы исходная матрица была невырожденной. Тогда

								A	A ...
								11	21
	1	1		~T	1		A12		A22 ...
A				A			... ... ...
A				A

			A			A
								A1n	A2n ...
								A1n	A2n ...

An1 An2

...

Ann


	A
	11
	A

A12



		A

...

	A1n
	A

A				A
21	...			n1
A	...			A
A				A
A				A
22		...		n2
		...			,
A				A	,
... ...				...
A2n			...	Ann
A			...
A				A

то есть ее элементами являются алгебраические дополнения к элементам транспонированной матрицы A , деленные на ее определитель. Отметим, что обратная матрица A 1 определена однозначно т.е. существует только одна обратная матрица для заданной квадратной невырожденной матрицы

Рассмотрим систему трех уравнений с тремя неизвестными:

x	10x 7x			10;
1		2	3
10x1 9x2			10x3 17;
8x		17x	x	8.
	1	2	3

Используя правило умножения (n n) матрицы и вектор столбца размера n 1, запишем исходную систему линейных уравнений в виде

AX B,

где

	1		10	7			x1			10
A	10		9 10		,	X	x	,	B	17		.
							2
		8	17	1							8
		8	17	1			x3				8

Поскольку по определению обратной матрицы A 1 имеем

A 1 ( AX ) A 1B EX A 1B ,

и так как EX X , решение системы можно записать в виде

X A 1B .
где		A ( 1)i j M					ij		–		алгебраические							дополнения элементов a
			ij				ij																		ij
матрицы A (заметим,								что алгебраические дополнения элементов строк
записываются в соответствующие столбцы). Получаем:

A			9	10		161 ,			A				10		10	70 ,	A		10			9		98,
11			17		1				12				8		1		13		8			17
			17		1								8		1				8			17
				7										1	7					1		10
A			10	7		129 ,			A					1	7	57 ,	A			1		10	63 ,
21			17		1				22					8	1		23			8		17
			17		1									8	1					8		17
				7								1			7						1	10
A			10	7		163 , A						1			7	80 ,	A				1	10			91.
31			9	10					32			10			10		33				10	9
			9	10								10			10						10	9
Обратная матрица, следовательно, имеет вид
				161 129						163
1	1
A					70			57		80			.
A		147			70			57		80			.
					98			63		91
					98			63		91

2.1 ВАРИАНТЫ ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ТЕМЕ «ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ»

Задание 1.

Найти матрицу D k M N F , если известны матрицы M , N , F и число k .

		3	0	4			1

1.	M	2	2	3 ,			N	0
		1	1	2				5
		1	1	2				5
	7		1	3				4

2.	M	5	1	2		,	N	2
		0	1	4				3
		0	1	4				3
		0	1	2				1

3.	M	3	1	2	,		N	2
		3	3	2				3
		3	3	2				3
	1		0	2				4

4.	M	3	1 2			,	N	1
		5	4	1				5

		1	5	4			5

5.	M	2	2	4		,	N	0
		1	1	2				2
		1	1	2				2


1		2				1	0		1

1		2	,	F		2	1		2		,	k 2 .
3		1				1	1		2

1		2				1	0		3

0		2	,	F		1	2		4		,	k 2 .
1		2				1	2	4
1		2				1	2	4
3	0					3	1	0

2	4	,		F	2		1	3 ,				k 3 .
1	1					5	1	2

0	2				1		1		2
1				F				2				k 3 .
1		3 ,		F		0	1	2		,		k 3 .
1	2					5	5		0
1	2					5	5		0
1		2				1	0		4

3 1 ,				F		2	2		3 ,			k 4 .
3		1				3	7		2

	1		1 2				3 1		4					1		1

6.	M	3	5 2	,	N		3	2	0	,	F			4		0
		5	3 1				1 1		2					2 4

	1		0		4			3		1	2					3

7.	M	2	3		1 ,	N		0	6 2				,	F		2
		1	1					2	3		0					1
		1	1		5			2	3		0					1
		1	1		2			1	2		2			1

8.	M	0	1		2 ,	N		1	2 3 ,					F		5
		1	3					1	1
		1	3		3			1	1		2			5
		3	3		4			1	1		1					4
		3	3		4			1	1		1					4

9.	M	2	4		3 ,		N	0	1		2	,		F		2
		1	3		0			5	3 4						1
		1	3		0			5	3 4						1

2 , k 4 .

5		4
			k 5 .
0		3 ,	k 5 .
1
1		4
1	3
			k 5 .
0	2 ,		k 5 .
3
3	1
0	1
0	1

3	3 ,		k 1 .
1	2
1	2

	1			1		2					2

10.	M	0		2		1 ,			N		3
		5		3		1					4

		0		3		4					1

11.	M	1		2		2		,		N	2
		1		1		2					5
		1		1		2					5
	7			1		3					4

12.	M	5		1		2		,		N	2
		0		1		4					3
		0		1		4					3
		0		1		2					1

13.	M	3		1		2	,		N		2
		3		3		2					3
		3		3		2					3
	1			0		2					4

14.	M	3		1		2		,		N	1
		5		4		1					5

		1		5		4				5

15.	M	2		2		4		,		N	0
		1		1		2					2
		1		1		2					2
		1	1	2						3 1

16.	M	3	5	2	,	N				3	2
		5	3							1	1
		5	3	1						1	1
	1			0		4					3

17.	M	2		3		1 ,			N		0
		1		1		5					2
		1		1		5					2
		1		1		2					1

18.	M	0		1		2	,		N		1
		1		3							1
		1		3		3					1

0	4						2	1	2

1	3 ,				F	1		0	4		,			k 6 .
1	5						1	3	1

0		2					3	0		3

1		7	,		F		1	2		3 ,				k 3.
3		1					1	2	1

1		2					1	0			3

0		2		,	F		1	2			4		,	k 2 .
1		2					1	2	4
1		2					1	2	4
3	0						3	1	0

2	4	,			F	2		1	3 ,					k 3 .
1	1						5	1	2

0		2				1		1		2

1 3 ,					F		0	1		2		,		k 3 .
1		2					5	5		0
1		2					5	5		0

	1	2			1

	3	1 ,		F	2
	3				3
	3	1			3
4				1	1
		F		4
0	,	F		4	0
2				2 4
2				2 4
	1	2			3

6		2	,	F	2
3		0			1
3		0			1
2		2		1

2		3 ,		F	5
1
1		2		5

0		4
			k 4 .
2		3 ,
7		2

2
		k 4 .
2	,

3
5		4
			k 5 .
0		3 ,
	1	4

1		3
			k 5 .
0		2 ,
3
		1

1 / 21 2 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.01.2021364.7 Кб12217.pdf
#
08.01.2021364.88 Кб12218.pdf
#
08.01.2021364.89 Кб12219.pdf
#
08.01.2021174.98 Кб3222.pdf
#
08.01.2021365.26 Кб12220.pdf
#
08.01.2021365.42 Кб22221.pdf
#
08.01.2021365.6 Кб12223.pdf
#
08.01.2021365.63 Кб32224.pdf
#
08.01.2021365.81 Кб42225.pdf
#
08.01.2021365.88 Кб52226.pdf
#
08.01.2021366.18 Кб12227.pdf

		3	0	4			1

1.	M	2	2	3 ,			N	0
		1	1	2				5
		1	1	2				5
	7		1	3				4

2.	M	5	1	2		,	N	2
		0	1	4				3
		0	1	4				3
		0	1	2				1

3.	M	3	1	2	,		N	2
		3	3	2				3
		3	3	2				3
	1		0	2				4

4.	M	3	1 2			,	N	1
		5	4	1				5

		1	5	4			5

5.	M	2	2	4		,	N	0
		1	1	2				2
		1	1	2				2

	1			1		2					2

10.	M	0		2		1 ,			N		3
		5		3		1					4

		0		3		4					1

11.	M	1		2		2		,		N	2
		1		1		2					5
		1		1		2					5
	7			1		3					4

12.	M	5		1		2		,		N	2
		0		1		4					3
		0		1		4					3
		0		1		2					1

13.	M	3		1		2	,		N		2
		3		3		2					3
		3		3		2					3
	1			0		2					4

14.	M	3		1		2		,		N	1
		5		4		1					5

		1		5		4				5

15.	M	2		2		4		,		N	0
		1		1		2					2
		1		1		2					2
		1	1	2						3 1

16.	M	3	5	2	,	N				3	2
		5	3							1	1
		5	3	1						1	1
	1			0		4					3

17.	M	2		3		1 ,			N		0
		1		1		5					2
		1		1		5					2
		1		1		2					1

18.	M	0		1		2	,		N		1
		1		3							1
		1		3		3					1

		3	0	4			1

1.	M	2	2	3 ,			N	0
		1	1	2				5
		1	1	2				5
	7		1	3				4

2.	M	5	1	2		,	N	2
		0	1	4				3
		0	1	4				3
		0	1	2				1

3.	M	3	1	2	,		N	2
		3	3	2				3
		3	3	2				3
	1		0	2				4

4.	M	3	1 2			,	N	1
		5	4	1				5

		1	5	4			5

5.	M	2	2	4		,	N	0
		1	1	2				2
		1	1	2				2

	1			1		2					2

10.	M	0		2		1 ,			N		3
		5		3		1					4

		0		3		4					1

11.	M	1		2		2		,		N	2
		1		1		2					5
		1		1		2					5
	7			1		3					4

12.	M	5		1		2		,		N	2
		0		1		4					3
		0		1		4					3
		0		1		2					1

13.	M	3		1		2	,		N		2
		3		3		2					3
		3		3		2					3
	1			0		2					4

14.	M	3		1		2		,		N	1
		5		4		1					5

		1		5		4				5

15.	M	2		2		4		,		N	0
		1		1		2					2
		1		1		2					2
		1	1	2						3 1

16.	M	3	5	2	,	N				3	2
		5	3							1	1
		5	3	1						1	1
	1			0		4					3

17.	M	2		3		1 ,			N		0
		1		1		5					2
		1		1		5					2
		1		1		2					1

18.	M	0		1		2	,		N		1
		1		3							1
		1		3		3					1

		3	0	4			1

1.	M	2	2	3 ,			N	0
		1	1	2				5
		1	1	2				5
	7		1	3				4

2.	M	5	1	2		,	N	2
		0	1	4				3
		0	1	4				3
		0	1	2				1

3.	M	3	1	2	,		N	2
		3	3	2				3
		3	3	2				3
	1		0	2				4

4.	M	3	1 2			,	N	1
		5	4	1				5

		1	5	4			5

5.	M	2	2	4		,	N	0
		1	1	2				2
		1	1	2				2

	1			1		2					2

10.	M	0		2		1 ,			N		3
		5		3		1					4

		0		3		4					1

11.	M	1		2		2		,		N	2
		1		1		2					5
		1		1		2					5
	7			1		3					4

12.	M	5		1		2		,		N	2
		0		1		4					3
		0		1		4					3
		0		1		2					1

13.	M	3		1		2	,		N		2
		3		3		2					3
		3		3		2					3
	1			0		2					4

14.	M	3		1		2		,		N	1
		5		4		1					5

		1		5		4				5

15.	M	2		2		4		,		N	0
		1		1		2					2
		1		1		2					2
		1	1	2						3 1

16.	M	3	5	2	,	N				3	2
		5	3							1	1
		5	3	1						1	1
	1			0		4					3

17.	M	2		3		1 ,			N		0
		1		1		5					2
		1		1		5					2
		1		1		2					1

18.	M	0		1		2	,		N		1
		1		3							1
		1		3		3					1