
1949
.pdfФедеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования «Воронежская государственная лесотехническая академия»
МАТЕМАТИКА
Уравнения математической физики Индивидуальные задания для студентов 2 курса специальности 190601 – Автомобили и автомобильное хозяйство
Воронеж 2009
2
УДК 517.958
Зюкин, П. Н. Математика. Уравнения математической физики [Текст] : индивидуальные задания для студентов 2 курса специальности 190601 – Автомобили и автомобильное хозяйство / П. Н. Зюкин, И. В. Сапронов ; Фед. агентство по образованию, ГОУ ВПО «ВГЛТА». – Воронеж, 2009. – 23 с.
Печатается по решению учебно-методического совета ГОУ ВПО «ВГЛТА» (протокол № 8 от 11 июня 2009 г.)
Рецензент д-р физ.-мат. наук, зав. кафедрой математического моделирования ВГУ, проф. В. А. Костин
3
РЕШЕНИЕ ПЕРВОЙ СМЕШАННОЙ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ
Рассмотрим первую смешанную задачу для уравнения теплопроводности: найти непрерывную на прямоугольнике 0 ≤ x ≤ A, 0 ≤ x ≤ T функцию u(x; t), удовлетворяющую уравнению теплопроводности
∂u |
= a |
2 |
∂ |
2u |
(a |
2 |
= const > 0) |
(1) |
∂t |
|
∂x2 |
|
|||||
|
|
|
|
|
|
|||
при 0 < x < A, 0 < t ≤ T, начальному условию |
|
|
|
|
||||
u(x; 0) = f(x), |
0 ≤ x ≤ A, |
(2) |
||||||
и граничным условиям |
|
|
|
|
|
|
|
|
u(0; t) = φ(t), |
|
0 ≤ t ≤ T, |
|
|
|
(3) |
||
u( A; t) = ψ(t), |
|
0 ≤ t ≤ T, |
|
|
(4) |
|||
где f(x), φ(t), ψ(t) – заданные функции.
Будем предполагать, что функции f(x), φ(t), ψ(t) непрерывны на соответствующих отрезках и f(0) = φ(0), f(A) = ψ(0). Эти условия вытекают из требования непрерывности функции u(x; t) на границе прямоугольника
0 ≤ x ≤ A, 0 ≤ t ≤ T.
Пусть n и m – фиксированные натуральные числа. Обозначим h = nA, τ= mT .
Числа h, τ называют шагами по осям Ox, Ot соответственно. В прямоугольнике 0 ≤ x ≤ A, 0 ≤ t ≤ T построим сетку, проведя прямые с уравнениями x = i · h,
t = k · τ (i = 0, 1, …, n; k = 0, 1, …, m) (рис.1).
|
t |
|
|
|
T |
(i, k+1) |
|
|
|
|
|
τ |
(i-1, k) |
(i, k) |
(i+1, k) |
|
|
|
O |
h |
A |
x |
|
|
||
|
|
Рис. 1 |
|
Введем обозначения |
|
|
|
|
xi = i · h , i = 0, 1, …, n; |
|
|
|
tk = k · τ, k = 0, 1, …, m; |
|
|
ui,k = u(xi; tk), |
i = 0, 1, …, n; k = 0, 1, …, m. |
|
|

4
Будем интересоваться только значениями ui,k функции u(x; y) в узлах (xi; tk)
сетки, i = 0, 1, …, n; k = 0, 1, …, m.
Считая h и τ малыми и заменяя в уравнении (1) приближенно частные
производные |
∂u |
|
и |
∂2u |
в каждом узле (xi; tk) сетки (i = 1, 2, …, n – 1; |
|||||||||||||||||
∂t |
|
∂x2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k = 0, 1, …, m – 1) конечными разностями |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
∂u(xi ; tk ) ≈ |
ui,k +1 − ui,k |
, |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
∂2u(x |
|
|
∂t |
|
|
|
|
|
τ |
|
|
|
|
|
|
|
||||
|
|
; t |
|
) |
|
|
ui +1,k − |
2ui,k |
|
+ ui −1,k |
|
|
|
|
||||||||
|
|
|
|
i |
|
k |
|
≈ |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|
|||||||
получаем |
|
|
∂x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
ui,k +1 − ui,k |
|
|
|
ui +1,k − 2ui,k + ui −1,k |
|
|
||||||||||||||
|
|
|
≈ a2 |
. |
|
|||||||||||||||||
|
|
|
|
τ |
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
|
|||
Отсюда получаем расчетную формулу |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
ui,k +1 |
= (1− |
2τa |
2 |
|
|
+ |
a2τ |
(ui−1,k |
+ ui+1,k ) . |
(5) |
||||||||||
|
|
|
h2 |
)ui,k |
h2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
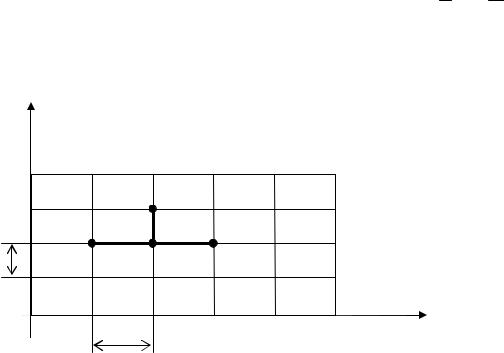
Для каждого узла (xi; tk) сетки (i =1, 2, …, n – 1; k = 0, 1, …, m – 1) формула
(5) соответствует набору узлов (шаблону), состоящему из четырех узлов, выделенных на рис. 1. С помощью этой формулы можно, зная значения функции u(x; t) в узлах с ординатой tk (эти узлы образуют k-й слой сетки), вычислить значение функции u(x; t) в любом узле (xi; tk+1) сетки с ординатой tk+1
(узле (k + 1) – го слоя) при i = 1, 2, …, n – 1.
Начальное условие (2) позволяет найти значения функции u(x; t) во всех узлах (xi; 0) (i = 0, 1, …, n) сетки:
ui,0 = u(xi; 0) = f(xi), i = 0, 1, …, n.
По формуле (5) находим значения функции u(x; t) в узлах (xi; t1), i = 1, …, n – 1, сетки. Значения искомой функции в крайних узлах (0; t1), ( A; t1) находим, пользуясь граничными условиями (3), (4). Переходя последовательно от одного слоя к другому, следующему выше, слою, определим значения искомого решения во всех узлах сетки.
Предлагаемый алгоритм решения задачи применим, если шаги h и τ выбраны так, что выполняется неравенство
τ≤ h2 . 2a2
При переходе к формуле (5) значения ui,k для i = 1, 2, …, n – 1; k = 1, 2, …, m становятся приближенными значениями соответствующих искомых значений
u(xi; tk) функции u(x; t).
В случае, когда
τ= h2 , 2a2
5
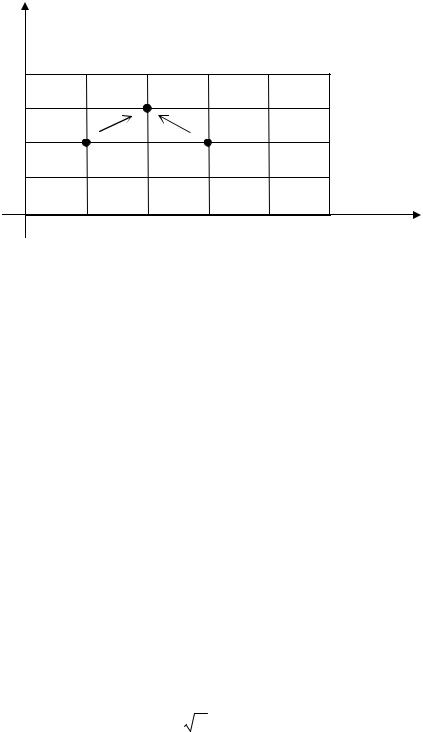
формула (5) имеет особенно удобный для вычислений вид
ui,k +1 = |
1 |
(ui−1,k + ui+1,k ). |
(6) |
|
2 |
|
|
Формула (6) соответствует набору узлов (шаблону), состоящему из трех узлов, выделенных на рис. 2.
t
|
(i, k+1) |
(i-1, k) |
(i+1, k) |
O |
x |
Рис.2
Индивидуальные задания
Используя метод конечных разностей, составить приближенное решение первой смешанной задачи для уравнения теплопроводности
|
∂u |
=a |
2 ∂2u |
, |
|
∂t |
∂x2 |
||
|
|
|
||
удовлетворяющее условиям |
|
|
|
|
u(x; 0) = f(x), |
|
0 ≤ x ≤ A, |
||
u(0; t) |
= φ(t), |
|
0 ≤ t ≤ T, |
|
u( A; t) |
= ψ(t), |
|
0 ≤ t ≤ T. |
|
Значения a2, A, T и функции f(x), φ(t), ψ(t) заданы в табл. 1.
Решение выполнить с шагом h по оси Ox, равным 0,2, и с четырьмя десятичными знаками.
|
|
|
|
|
|
Таблица 1 |
|
№ |
а2 |
A |
T |
f(x) |
φ(t) |
|
ψ(t) |
варианта |
|
|
|
|
|
|
|
1 |
1 |
1 |
0,12 |
x2 – x |
0 |
20t |
|
2 |
1 |
1 |
0,12 |
1 – x2 |
1 |
100t2 |
|
3 |
1 |
1 |
0,12 |
x +1 |
20t + 1 |
2 |
|
4 |
1 |
1 |
0,12 |
x |
0 |
1 |
– 10t2 |
5 |
1 |
1 |
0,12 |
2x |
t |
2 |
– t |
6 |
2 |
1 |
0,06 |
x(x + 1) |
0 |
3t + 2 |
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
Окончание табл. 1 |
||
№ |
а2 |
A |
T |
f(x) |
|
φ(t) |
|
ψ(t) |
варианта |
|
|
|
|
|
|
|
|
7 |
2 |
1 |
0,06 |
2 + x2 |
2 |
– t |
3 |
|
8 |
2 |
1 |
0,06 |
x(3x – 1) |
0 |
|
2 |
+ t |
9 |
2 |
1 |
0,06 |
x2 |
2t |
1 |
|
|
10 |
1 |
1,2 |
0,1 |
2 |
2 |
– t |
2 |
+ 10t |
11 |
1 |
1,2 |
0,1 |
1 |
1 |
|
1 |
+ 10t |
12 |
1 |
1,2 |
0,1 |
2x |
– t |
2,4 + 4t |
||
13 |
1 |
1,2 |
0,1 |
x2 |
0 |
|
1,44 + 8t |
|
14 |
2 |
1,2 |
0,05 |
0 |
t |
|
20t |
|
15 |
2 |
1,2 |
0,05 |
2x + 1 |
3t |
3,4 – 50t |
||
16 |
2 |
1,2 |
0,05 |
x2 |
0 |
|
60t + 1,44 |
|
17 |
2 |
1,2 |
0,05 |
1 – 2x |
1 |
+ 30t |
– 1,4 |
|
18 |
1 |
0,8 |
0,14 |
– 1 |
– t – 1 |
50t – 1 |
||
19 |
1 |
0,8 |
0,14 |
x |
2t2 |
0,8 – 20t |
||
20 |
1 |
0,8 |
0,14 |
x(0,8 – x) |
– 2t |
– t |
||
21 |
1 |
0,8 |
0,14 |
– x |
4t |
t – 0,8 |
||
22 |
2 |
0,8 |
0,07 |
3 |
3 |
– 100t |
3 |
+ t |
23 |
2 |
0,8 |
0,07 |
1 – 2x |
1 |
|
40t – 0,6 |
|
24 |
2 |
0,8 |
0,07 |
x2 + 3 |
3 |
+ t |
3,64 – 100t |
|
25 |
2 |
0,8 |
0,07 |
2x – 1 |
– 1 |
3t + 0,6 |
||
Пример выполнения задания
Используя метод конечных разностей, составить приближенное решение первой смешанной задачи для уравнения теплопроводности
∂u = 2 ∂2u , ∂t ∂x2
удовлетворяющее условиям |
|
3 |
|
||
u(x; 0) = x( |
− x ), 0 ≤ x ≤ 1, |
||||
|
|
|
|
2 |
|
u(0; t) = 0, |
|
0 ≤ t ≤ 0,04, |
|||
u(1; t) = |
1 |
|
, |
|
0 ≤ t ≤ 0,04. |
|
|
||||
2 |
|
|
|
|
|
Решение выполнить при h = 0,2 с двумя десятичными знаками.
Решение. Шаг по оси Ot выберем исходя из условия τ = |
h2 |
, |
поэтому |
|||||
2a |
2 |
|||||||
|
(0,2)2 |
|
|
|
||||
τ = |
=0,01. При таком выборе τ расчеты будем вести по формуле (6). |
|||||||
2 |
2 |
|||||||
|
|
|
|
|
|
|||
7
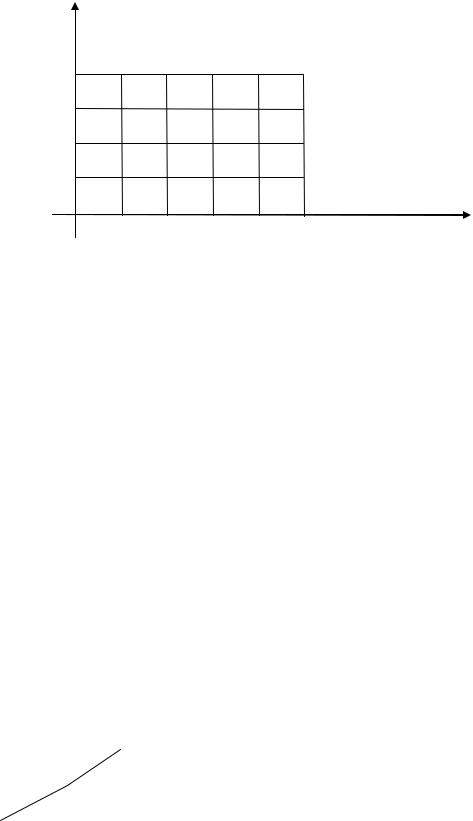
Построим прямоугольник, в котором разыскивается решение, покроем его сеткой, проведя прямые с уравнениями x = ih (i = 0, 1, 2, 3, 4, 5) и t = kτ
( k = 0, 1, 2, 3, 4), и проведем нумерацию узлов сетки (рис. 3). y
0,04 |
(0,4) |
(1,4) |
(2,4) |
(3,4) |
(4,4) |
(5,4) |
|
|
|
|
|
|
|
|
|
0,03 |
(0,3) |
(1,3) |
(2,3) |
(3,3) |
(4,3) |
(5,3) |
|
|
|
|
|
|
|
|
|
0,02 |
(0,2) |
(1,2) |
(2,2) |
(3,2) |
(4,2) |
(5,2) |
|
|
|
|
|
|
|
|
|
0,01 |
(0,1) |
(1,1) |
(2,1) |
(3,1) |
(4,1) |
(5,1) |
|
|
|
|
|
|
|
|
|
|
(0,0) |
(1,0) |
(2,0) |
(3,0) |
(4,0) |
(5,0) |
|
O |
|
0,2 |
0,4 |
0,6 |
0,8 |
1 |
x |
|
|
|
|
Рис. 3 |
|
|
|
В крайних левых и правых узлах сетки из |
граничных условий получаем |
||||||
u0,0 = u0,1 = u0,2 = u0,3 = u0,4 = 0; u5,0 = u5,1 = u5,2 = u5, 3= u5,4 = 0,5.
Из начального условия находим значения функции u(x; t) в узлах нулевого слоя:
u1,0 = 0,26; u2,0 = 0,44; u3,0 = 0,54; u4,0 = 0,56.
В дальнейшем расчеты ведутся по формуле (6). Для узлов первого слоя:
u1,1 = 0,22; u2,1 = 0,40; u3,1 = 0,50; u4,1 = 0,52.
Для узлов второго слоя:
u1,2 = 0,20; u2,2= 0,36; u3,2 = 0,46; u4,2= 0,50.
Для узлов третьего слоя:
u1,3 = 0,18; u2,3 = 0,33; u3,3 = 0,43; u4,3 = 0,48.
Для узлов четвертого слоя:
u1,4 = 0,17; u2,4 = 0,31; u3,4 = 0,41; u4,4 = 0,47.
Полученные значения представим в табл. 2.
Таблица 2
4 |
0,04 |
0 |
0,17 |
0,31 |
0,41 |
0,47 |
0,5 |
3 |
0,03 |
0 |
0,18 |
0,33 |
0,43 |
0,48 |
0,5 |
2 |
0,02 |
0 |
0,20 |
0,36 |
0,46 |
0,50 |
0,5 |
1 |
0,01 |
0 |
0,22 |
0,40 |
0,50 |
0,52 |
0,5 |
0 |
0 |
0 |
0,26 |
0,44 |
0,54 |
0,56 |
0,5 |
|
tk |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
|
xi |
|
|
|
|
|
|
k |
|
0 |
1 |
2 |
3 |
4 |
5 |
i |
|
|
|
|
|
|
|
8
РЕШЕНИЕ ЗАДАЧИ ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ ЛАПЛАСА В ПРЯМОУГОЛЬНИКЕ МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ
Пусть ABCD – прямоугольник с вершинами A(0; 0), B (0; b), C(a; b), D(a; 0),
где a > 0, b > 0. Задача Дирихле для уравнения Лапласа в прямоугольнике ABCD ставится следующим образом.
Требуется найти непрерывную на прямоугольнике ABCD функцию u(x; y) (x [0, a], y [0, b]), удовлетворяющую внутри этого прямоугольника
уравнению Лапласа
∂2u |
+ |
∂2u |
= 0 |
(7) |
|
∂x2 |
∂y2 |
||||
|
|
|
и принимающую на границе прямоугольника заданные значения, то есть
u |
AB |
= u(0; y) = f1(y), |
y [0, b], |
|
|
|
|
|
= u(x; b) = f2 (x), |
|
|
u |
BC |
x [0, a], |
|
||
|
|
|
= u(a; y) =f3 (y), |
|
|
u |
CD |
y [0, b], |
(8) |
||
u |
|
AD |
= u(x; 0) =f4 (x), |
x [0, a], |
|
|
|
||||
где f1(y), f2 (x), f3(y), f4(x) – заданные функции. |
|
||||
Будем предполагать, что функции f1(y), f2 (x), f3(y), f4(x) непрерывны на соответствующих отрезках и f1(0) = f4(0), f1(b) = f2(0), f2(a) = f3(b), f3(0) = f4(a).
Эти условия вытекают из требования непрерывности функции u(x; y) на границе прямоугольника ABCD.
Пусть |
n |
и |
m – |
фиксированные натуральные числа. Обозначим |
|||
h = |
a |
, τ = |
b |
. Числа h, τ |
называют шагами по осям Ox, Oy соответственно. В |
||
n |
m |
||||||
|
|
|
|
|
|||
прямоугольнике ABCD построим сетку, проведя прямые с уравнениями x = i · h, y = j ·τ (i = 0, 1, …, n; j = 0, 1, …, m) (рис. 4).
y |
|
|
|
|
b |
B |
|
|
C |
|
(i, j+1) |
|
|
|
|
|
|
|
|
τ |
(i-1, j) |
(i, j) |
(i+1, j) |
|
|
|
|
|
|
|
A |
(i, j-1) |
|
D |
|
|
|
||
O |
h |
|
a |
x |
Рис. 4
9
Введем обозначения:
xi = i · h, i = 0, 1, …, n; yј = j ·τ, j = 0, 1, …, m;
ui,j = u(xi; yj), i = 0, 1, …, n; j = 0, 1, …, m.
Будем интересоваться только значениями ui,j функции u(x; y) в узлах (xi; yj)
сетки, i = 0, 1, …, n; j = 0, 1, …, m.
Считая h и τ малыми и заменяя в уравнении (7) приближенно частные
производные |
∂2u |
и |
∂2u |
|
|
в каждом |
внутреннем узле (xi; yj) |
сетки |
|||||||||||||
∂x2 |
∂y2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
конечными разностями |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
∂2u(xi ; y j ) |
≈ |
|
|
ui +1, j |
− 2ui, j + ui −1, j |
, |
|
||||||||||
|
|
|
|
|
|
∂x2 |
|
|
|
|
|
|
|
h2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∂2u(xi ; y j ) |
|
≈ |
|
ui, j+1 |
− 2ui, j + ui, j−1 |
, |
|
|||||||||
|
|
|
|
|
|
∂y2 |
|
|
|
|
|
τ2 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ui +1, j − 2ui, j + ui −1, j |
+ |
|
|
ui, j+1 −2ui, j |
+ ui, j−1 |
= 0 |
(9) |
|||||||||||||
|
|
|
h2 |
|
|
|
|
|
|
|
τ2 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
для i = 1, 2, …, n – 1; j = 1, 2, …, m – 1. |
|
|
|
|
|
|
|||||||||||||||
Подставляя координаты каждого граничного узла в условия (8), получаем |
|||||||||||||||||||||
|
|
u0, j |
= f1(y j ), |
j =0,1, ..., m, |
|
|
|
|
|
||||||||||||
|
|
ui,m |
=f2 (xi ), |
i =1, 2, ..., n −1, |
|
|
|
|
|
||||||||||||
|
|
un, j |
=f3 (y j ), |
j = 0,1, ..., m, |
|
|
|
|
(10) |
||||||||||||
|
|
ui,0 |
=f4 (xi ), |
i =1, 2, ..., n −1. |
|
|
|
|
|
||||||||||||
Система линейных алгебраических уравнений (9), (10) называется разностной схемой для задачи (7), (8). При переходе к системе уравнений (9), (10) значения ui,j для внутренних узлов сетки становятся приближенными. Для определения величин ui,j требуется решить систему уравнений (9), (10).
В случае, когда шаги h и τ по осям Ox и Oy равны (h = τ), уравнения (9) имеют наиболее простой вид
ui, j = 1 (ui−1, j + ui, j+1 + ui+1, j + ui, j−1) |
|
(10′) |
|||
4 |
|
|
|
|
|
для i = 1, 2, …, n – 1; j = 1, 2, …, m – 1. |
|
|
|
|
|
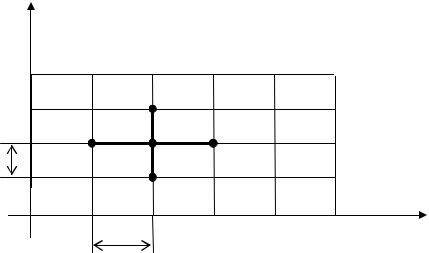
Каждое из уравнений (10′) ( |
(9) при h ≠ |
τ) соответствует набору узлов |
|||
(шаблону), состоящему из пяти |
узлов, |
выделенных на рис. |
4 с |
помощью |
|
«креста». |
|
|
в граничных |
узлах, |
поэтому |
Равенства (10) определяют значения |
ui,j |
||||
неизвестными являются лишь значения ui,j, i = 1, 2, …, n – 1; j = 1, 2, …, m – 1, во внутренних узлах. Эти значения составляют решение системы уравнений
(10′) ( (9) при h ≠ τ).

10
Будем предполагать далее, что h = τ. Система уравнений (10′) решается приближенно итерационным методом Зейделя, который состоит в построении последовательности итераций вида
u(k) |
= 1 |
(u(k) |
+ u(k) |
+ u(k −1) + u(k −1) ), |
(11) |
|
i, j |
4 |
i−1, j |
i, j+1 |
i+1, j |
i, j−1 |
|
где верхним индексом |
k обозначен номер итерации, при этом предполагается, |
|||||
что для граничных узлов значения |
ui(,0j) = ui(,kj) = ui, j |
(k =1, 2, ... ) определены |
||||
равенствами (10). Значения ui(,0j) для внутренних узлов могут быть определены
каким-либо способом. Для каждой итерации формула (11) применяется, начиная с левого верхнего внутреннего узла, затем для соседнего справа внутреннего узла, и т. д., затем для внутренних узлов следующей горизонтали
слева направо, и т. д. Известно, что ui(,kj) → ui, j при k →∞для каждой пары значений i, j, где i = 1, 2, …, n – 1; j = 1, 2, …, m – 1.
Построение последовательности итераций ui(,kj) завершается, если для всех внутренних узлов значения ui(,kj) и ui(,kj−1) отличаются меньше, чем на ε, где
ε – заданная точность решения, то есть если
ui(,kj) − ui(,kj−1) < ε
для i = 1, 2, …, n – 1; j = 1, 2, …, m – 1.
Индивидуальные задания
Используя метод конечных разностей, составить приближенное решение задачи Дирихле для уравнения Лапласа
∂2u + ∂2u = 0 ∂x2 ∂y2
впрямоугольнике с вершинами A(0; 0), B(0; b), C(a; b), D(a; 0) с точностью
ε=0,01 для шага h = 0,2. Значения a, b и значения функции u(x; y) на границе
прямоугольника ABCD заданы в табл. 3.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 |
|
№ |
а |
b |
u |
|
|
u |
|
|
u |
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
варианта |
|
|
|
AB |
|
BC |
|
CD |
|
AD |
|
||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
||||||||||
1 |
1 |
0,8 |
0,5y2 + 6 |
1,48x + 6,32 |
y + 7 |
x + 6 |
|
||||||||
2 |
0,8 |
1 |
y + 4 |
1,5x + 5 |
0,6y2 + 5,6 |
2x + 4 |
|
||||||||
3 |
1 |
0,8 |
4y |
0,28x2 + 3,2 |
0,6y + 3 |
3x |
|
||||||||
4 |
0,8 |
1 |
2y + 1 |
x + 3 |
2,48y + 1,32 |
0,5x2 + 1 |
|
||||||||
5 |
1 |
0,8 |
0,3y + 7,1 |
0,1x + 7,34 |
0,375y2 + 7,2 |
0,1x + 7,1 |
|
||||||||
