291

3

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ВОРОНЕЖСКАЯ ГОСУДАРСТВЕННАЯ ЛЕСОТЕХНИЧЕСКАЯ АКАДЕМИЯ

ОСНОВЫ ТЕОРИИ НАДЕЖНОСТИ И ДИАГНОСТИКА Методические указания к выполнению

лабораторных работ для студентов специальностей 150200 – Автомобили и автомобильное хозяйство, 240400 – Организация и безопасность движения

ВОРОНЕЖ 2002

4

УДК 630.36 Посметьев В.И. Основы теории надежности и диагности-

ка. Методические указания к выполнению лабораторных работ для студентов специальностей 150200 – Автомобили и автомобильное хозяйство и 240400 – Организация и безопасность движения/ Воронеж. гос. лесотехн. акад.; В.И. Посметьев, В.Л. Мурзинов, А.М. Кадырметов. Воронеж, 2002. – 24 с.

Представлена методика проведения лабораторных работ. Предложены многовариантные задания для самостоятельного выполнения. Предназначено для закрепления теоретических знаний по курсу «Основы теории надежности и диагностика».

Научный редактор – д-р техн. наук, проф. Посметьев В.И. Рецензент – заведующий кафедрой «Ремонт машин»

(ВГАУ), доцент, канд. техн. наук Чечин А. И.

Печатается по решению редакционно-издательского совета

Воронежской государственной лесотехнической академии

© Посметьев В.И., Мурзинов В.Л., Кадырметов А.М., 2002

© Воронежская государственная лесотехническая академия, 2002

5

1 ЦЕЛЬ РАБОТЫ Освоить теорию надежности и приобрести навыки приме-

нения ее результатов к решению прикладных вопросов надежности автомобилей, автомобильного хозяйства и оборудования.

2 ОБЩИЕ ПОЛОЖЕНИЯ Одним из факторов, сдерживающих повышение техниче-

ского уровня автомобилей, автомобильного хозяйства и оборудования, является недостаточная надежность и отсутствие системы испытаний на надежность в процессе изготовления опытного образца и в серийном производстве. Затраты на техническое обслуживание и ремонт оборудования очень высоки. Без методов и расчетов на основе теории надежности трудно установить момент остановки оборудования на ремонт и обслуживание. Современные методы определения и контроля показателей надежности, а также средства испытаний оборудования на надежность, позволяют повысить технический уровень оборудования автомобилей и автомобильного хозяйства.

3 ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ Основные понятия и определения надежности регламенти-

рованы стандартом. При изучении надежности технических устройств рассматриваются самые разнообразные объекты – машины, сооружения, аппаратура и др. В соответствии с государственными стандартами под понятием объект понимается предмет определенного назначения, рассматриваемый в период проектирования, производства, эксплуатации, исследований и испытаний на надежность.

Стандарт различает исправное и работоспособное состояние объекта. При исправном состоянии объект соответствует всем требованиям, установленным нормативно-технической документацией. В практике принято оценивать машины и оборудование не по исправному, а по работоспособному их состоянию. Одними из основных понятий в теории надежности являются:

– Работоспособность – это состояние объекта, при котором он способен выполнять заданные функции, сохраняя значе-

6

ния заданных параметров в пределах, установленных норма- тивно-технической документацией.

–Отказ – событие, заключающееся в нарушении работоспособного состояния объекта.

–Повреждение – событие, заключающееся в нарушении исправного состояния объекта при сохранении им работоспособного состояния.

–Сбой – самоустраняющийся отказ.

–Надежность – свойство объекта сохранять во времени в установленных пределах значения всех параметров, характеризующих способность выполнять требуемые функции в заданных режимах и условиях применения, технического обслуживания, ремонтов, хранения и транспортирования.

–Безотказность – свойство объекта непрерывно сохранять работоспособное состояние в течение некоторого времени или некоторой наработки.

–Долговечность – свойство объекта сохранять работоспособное состояние до наступления предельного состояния при установленной системе технического обслуживания и ремонта.

–Ремонтопригодность – свойство объекта, заключающееся в приспособленности к предупреждению и обнаружению причин возникновения отказов и повреждений, к поддержанию и восстановлению работоспособного состояния путем проведения технического обслуживания и ремонтов. Машины и оборудование лесного комплекса относятся к категории ремонтируемых машин.

–Сохраняемость – свойство объекта сохранять работоспособность в течение и после установленного срока хранения или транспортирования.

4 ХАРАКТЕРИСТИКИ ОСНОВНЫХ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

4.1 БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

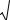
7

где X – дискретная случайная величина; Pm – вероятность появления случайной величины; m = 0, 1, …, n; – возможные значения случайной величины; n – количество независимых опытов; p – вероятность появления ожидаемого события в каждом независимом опыте; 0< p <1; q = 1 – p.

Математическое ожидание, дисперсия и среднеквадратическое отклонение в соответствии с классическим определением имеют вид

При использовании производящих функций формулы (1.2) и (1.3) можно представить в более простой записи

Если вероятность появления ожидаемого события в каждом независимом опыте различна, то

З а д а ч а 1 . Из лесного массива отправлено n = 5 лесовозов на лесопильные рамы. Каждый лесовоз может не доехать до места назначения с вероятностью p = 0.3 независимо от других лесовозов. Значением случайной величины Х здесь является

m– число не доехавших лесовозов. Найти:

1)вероятность того, что до места назначения доедет не менее

k = 2 лесовозов;

2)mx – наиболее вероятное число недоехавших лесовозов;

3)дисперсию и среднеквадратическое отклонение случайной величины Х.

8

Р е ш е н и е . Число недоехавших автомобилей распределено по биномиальному закону. По формуле (1.1) строим табл.1.1.

Таблица 1.1 – вероятности для различного количества недоехавших лесовозов

1) Вероятность того, что до места назначения доедет не менее двух лесовозов соответствует условию – до места назначения не доедет не более трех лесовозов. Используя данные табл. 1.1 запишем:

P{X ≤ 3}= P + P + P + P =

=0.168 + 0.360 + 0.309 + 0.133 = 0.970 .

2)Наиболее вероятное число недоехавших лесовозов соответствует математическому ожиданию случайной величины Х0 1 2 3

mx = n p = 5 0.3 = 1.5 ,

т.е. наиболее вероятно: до места назначения не доедет от 1 до 2-х лесовозов.

3) Dx = n p q = 5 0.3 0.7 = 1.05 σx = Dx = 1.05 = 1.03 О т в е т : P{X ≤ 3}= 0.970 , mx = 1.5 , Dx = 1.05 .

4.2 РАСПРЕДЕЛЕНИЕ ПУАССОНА

где X – дискретная случайная величина; Pm – вероятность появления случайной величины; m = 0, 1, 2,… – возможные значения случайной величины; а – параметр распределения Пуассона.

9

где λ – интенсивность потока событий; τ – время.

Используя производящие функции можно показать, что математическое ожидание и дисперсия случайной величины с распределением Пуассона равны между собой:

З а д а ч а 2 . На станцию технического обслуживания поступают автомобили с интенсивностью λ = 0.8 авт./час. Найти вероятность того, что за время τ=2 часа:

1)не поступит ни одного автомобиля;

2)поступит ровно m1 автомобилей, m1=1;

3)поступит хотя бы m2 автомобилей, m2=1.

Ре ш е н и е . Интенсивность потока поступления автомобилей величина постоянная, поэтому воспользуемся формулой (2.3) для определения параметра распределения Пуассона, т.е.

1) Для события, что не поступит ни одного автомобиля соответствует значение m = 0 и, используя формулу (2.1) и (2.5), получим вероятность этого события

P0 = 1.60 e−1.6 = 0.202 . 0!

2) Для события, что поступит ровно один автомобиль вероятность определиться следующим образом

m = 1, P1 = 1.16!1 e−1.6 = 0.323.

3)P{X ≥ 1}= 1− P{X = 0}= 1− P0 = 1− 0.202 = 0.798 .

От в е т : P0 = 0.202 , P1 = 0.323, P{X ≥ 1}= 0.798 .

10

З а д а ч а 3 . На автозаправочную станцию с 0 ч до 6 ч 40мин прибывают автомобили с интенсивностью потока, линейно зависящего от времени, т.е.

Поток прибытия автомобилей является пуассоновским нестационарным процессом. На основе статистических данных с учетом того, что 6 ч 40 мин = 400 мин дана интенсивность потока в начале и конце контролируемого временного интервала, т.е.

Найти вероятность P того, что за интервал времени от t1 = 195 мин (3 ч 15 мин) до t2 = 205 мин (3 ч 25 мин) поступит не менее

n=3 автомобилей.

Р е ш е н и е . Найдем значение коэффициентов В и С, входящих в формулу (2.6) из следующей системы уравнений

откуда В = 1/2000, С = 0.2. Воспользовавшись формулой (2.2), определим среднее число прибывших автомобилей в заданном интервале времени [195 мин, 205 мин]

Искомая вероятность определится из следующего соотношения с использованием формулы (2.1)

О т в е т : P{X ≥ 3}= 0.577 .

12

2)mx – наиболее вероятное число новых аккумуляторов в вы-

данной партии;

3)дисперсию и среднеквадратическое отклонение случайной величины Х.

Ре ш е н и е . Построим ряд распределения случайной величины Х, используя формулу (3.1).

Таблица 3.1 – вероятности для различного количества новых аккумуляторов в выданной партии.

1) Вероятность того, что в выданной партии аккумуляторов не менее трех новых соответствует условию, записанному на основании данных табл. 3.1:

P{X ≥ 3}= 1− (P0 + P1 + P2 ) =

=1− (0.008 + 0.159 + 0.476) = 0.643.

2)Наиболее вероятное число новых аккумуляторов в выданной партии соответствует математическому ожиданию случайной величины Х. Воспользуемся формулой (3.2)