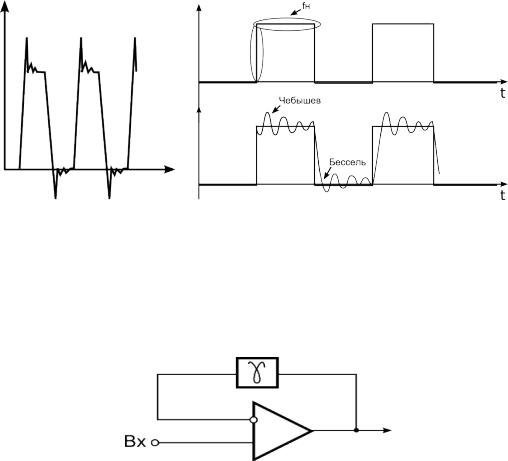
Если через фильтры проходит сигнал импульсный с широким спектром, то искажения
Рисунок 70: Фильтр |
Рисунок 71: |
Чебышева |
|
становятся сильно заметными. Фильтр Чебышева не используется для обработки импульсных сигналов.
Включение частотно зависимой цепи в цепь обратной связи усилителя
Рисунок 72:
γ = W = A(p)/B(p)
kос(p) = Uвых(p)/Uвх(p) = k0/(1+γk0) (отрицательная ОС) = k0/(1+A(p)/B(p)k0=k0B(p)/(B(p) +A(p)k0)=B(p)/A(p)
Схема с отрицательной обратной связью инвертирует коэффициент передачи цепи обратной связи. В теории для расчета (базовой схемы) используют обычно фильтры нижних частот. Их можно перевести и в полосовой и в режекторный фильтры. Также эти свойства схем с отрицательной обратной связью справедливы как для частотно зависимых гамма, так и для обычных.
Краткая теория активных фильтров
На примере фильтра нижних частот. В комплексной форме k(jw) = U`вых/U`вх = 1/(1+jwRC) k(p)=1/(1+pRC).
В теории фильтров используют нормированную переменную. P = p/wср = jw/wср = jΩ, Ω=w/wср. Нормированные частоты, относительно частоты среза.
Частота среза ФНЧ
fср = 1/2πRC, P=p/wср = jwRC=pRC. K(P) = 1/(1+P) — АЧХ ФНЧ в нормированной форме. Для последовательно включенных фильтров АЧХ имеет вид: K(P) = 1/((1+α1P)(1+α2P)...
29
(1+αnP). В виде полинома после преобразования знаменателя: K(P) = 1/(1+c1P+c2P^2+...+CnP^n) — форма 2.
Ci — действительные положительные коэффициенты. Порядок фильтра определяется максимальной степенью P.
Часто для расчета фильтров комплексную передаточную функцию записывают в форме сомножителей второго порядка. K(P) = k0/(1+a1P+b1P^2)(1+a2P+b2P^2)...(1+anP+bnP^2)
ai, bi — действительные положительные коэффициенты. АЧХ фильтров Баттерворта записывают в форме полиномов:
Порядок Полином
11+P
21+sqrt(2)P+P^2
31+2P+2P^2+P^3
Больше третьего порядка, фильтры, как правило, не используются. Для аппроксимации фильтра Баттерворта используется полином формы 2.
Фильтр Бесселя:
Порядок Полином
11+P
21+P+1/3P^2
3 |
1+P+2/5P^2+1/15P^3 |
|
|
|
|
K(p) = k0/П(1+a1P+b1P)^2 |
||
Фильтр Чебышева |
||
|
|
|
N |
|
полином |
1 |
|
T1(x) = x |
|
|
|
2 |
|
T2(x) = 2x^2-1 |
|
|
|
3 |
|
T3(x) = 4x^3-3x |
Полином Чебышева |k|^2 = g*k0^2/1+εTn(x)
ε - oпределяет относительную не равномерность характеристики фильтра. G — x = 0, |k|^2 = k0^2
kmax/kmin = sqrt(1+ε^2)
При расчетах фильтров и составлении схем, возможно много вариантов. Существует множество вариантов подачи обратной связи, обратные связи частотно зависимые, они имеют полюса и нули. Нули и полюса могут соотноситься друг с другом в разных пропорциях.
Для практического применения многообразие схем фильтров необходимо обеспечить, вопервых, относительно простую схему. Поэтому, на практике используются фильтры порядка не выше третьего. Для увеличения порядка требуемого фильтра используют метод каскадирования. Ограничения на порядок применяемого фильтра определяется сложностью математического описания, необходимостью аппроксимации, и вытекающие отсюда погрешности. Необходимо обеспечить независимость регулировки частот среза и коэффициентов передачи.
30