
2165
.pdf
Напрягаемая арматура А-ІV.
Характеристики арматуры:
Rs,ser= 590 МПа, Еs= 19 104 МПа.
Класс бетона по прочности на сжатие В22,5; передаточная прочность бетона принята Rвр= 13 МПа; начальный
модуль упругости бетона Ев= 25,5 103 МПа.
Натяжение арматуры осуществляется «на бетон» электротермическим способом.
Полная величина потерь предварительного напряжения арматуры равна сумме первых и вторых потерь:
loss |
loss1 |
loss2 . |
Согласно рекомендациям СНиПа[4] |
|
|
первые потери: |
|
|
loss1 3 |
4 , |
|
где 3 потери от деформации анкеров; 4 потери от трения арматуры о поверхность бетона.
Потери от деформации анкеров определяются по следующему равенству:
3 |
|
l1 l2 |
Es . |
|
|||
|
|
l |
|
Длина одного обжимного кольца
D 3,14 18 56,52м = 56520 мм.
Количество анкерных упоров для кольца – 4 (рис. 26).
Деформации на один анкерный упор
l1 l2 1 1 2мм.
Величина потерь от деформации анкеров
3 2 4 19 104 26,9МПа. 56520
Потери от трения арматуры о поверхность бетона 4 .
При натяжении арматуры электротермическим способом
4 = 0.
Первые потери
loss1 3 4 26,9 0 26,9МПа.
Вторые потери:
Согласно рекомендациям СНиПа [ 4 ]
loss2 7 8 9 11.
7 0,1 sp 20 потери от релаксации напряжения арматуры.
7 0,1 530 20 33МПа.
8 30МПа потери от ползучести бетона.
9 потери от ползучести бетона.
При определении потерь от ползучести считаем, что натяжение напрягаемой арматуры производится при передаточной прочности Rвр= 13 МПа, что соответствует:
классу бетона В22,5;
начальному модулю упругости бетона Ев= 25,5 103 МПа.
|
E |
s |
|
19,0 104 |
7,45. |
|
|
25,5 103 |
|||
|
Eв |
|
|||
Наибольшая площадь стержневой напрягаемой арматуры Аsp=763,5 мм2.
41

Ared A Asp 160 1000 7,45 763,5 165688,1 мм2.
Начальное усилие обжатия
P sp loss1 Asp 530 26,9 763,5 384116,9Н = 384,1 кН.
Напряжение в бетоне
P384117
вр Ared 165688 2,32МПа.
вр 2,32 0,18 0,75.
Rвр 13
Потери от ползучести бетона
9 150 1,00 0,18 27,0 МПа; 1,00 СНиП [4].
Потери от деформации обжатия стыков между блоками
11 |
|
n l |
Es , |
|
|||
|
|
l |
|
где n – число швов конструкции; l=0,3 мм– обжатие стыка; l – длина натягиваемой арматуры, мм.
Периметр резервуара l= D 3,14 18 56,52м = 56520 мм; ширина панели |
в = |
|
|
3,14 |
1,57м; число панелей |
|||
|
|
|||||||
|
|
|
|
2 |
2 |
|
||
2 D 2 18 36; количество швов 37. |
|
|
|
|
|
|||
Потери от деформации стыков |
|
|
|
|
|
|
|
|
|
11 |
37 0,3 |
19 104 37,3 МПа. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
56520 |
|
|
|
|
|
|
|
Вторые потери |
|
|
|
|
|
|
|
|
|
loss2 33 30 27 37,3 127,3 МПа. |
|
|
|
|
|
||
Полные потери |
|
|
|
|
|
|
|
|
loss |
loss1 loss2 26,9 127,3 154,2 МПа > 100 МПа. |
|||||||
Пример. Расчет стенки резервуара по образованию трещин.
Расчет стенки по образованию трещин выполняется по условию
N Ncrc .
Принимаем
Ncrc P,
где P sp sp loss Asp ; |
sp 1 sp . |
При электротермическом способе натяжения арматуры (СНиП [4])
|
|
|
|
p |
|
|
|
1 |
|
|
|
|
|
|
|||||
|
sp |
0,5 |
|
|
|
1 |
|
|
|
|
|
|
|
0,1; |
|
||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
sp |
|
|
|
|
np |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
p 384,1 МПа; |
|
|
|
sp 530 МПа; np |
4. |
||||||||||||||
|
|
|
384,1 |
|
|
1 |
|
|
|
|
|
|
|||||||
sp |
0,5 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0,54 0,1. |
|
|||
530 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|||||||||
Тогда
sp 1 0,54 0,46.
sp loss 530 154,2 375,8 МПа.
Расчет по образованию трещин выполняется для каждой условной зоны, на которые разбивается стенка по высоте
(см. рис. 14). Результаты расчета сводятся в табл. 9.
42
Таблица 9
Проверка условия трещинообразования
Номер |
|
sp sp loss , |
|
|
|
|
|
зоны |
Asp, |
Ncrc, |
Nk , |
Ncrc |
Nk |
|
|
(сверху |
мм2/пог.м |
МПа |
кН/пог.м |
кН/пог.м |
|
||
|
|
|
|||||
вниз) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
І |
254,5 |
|
95,64 |
70,04 |
95,64 > 70,04 |
|
|
|
|
|
|
|
|
|
|
ІІ |
509,0 |
|
191,28 |
139,70 |
191,28>139,70 |
|
|
|
|
375,8 |
|
|
|
|
|
ІІІ |
763,5 |
286,92 |
240,93 |
286,92>240,93 |
|
||
|
|
|
|
|
|
|
|
ІV |
763,5 |
|
286,92 |
247,02 |
286,92>247,02 |
|
|
|
|
|
|
|
|
|
|
V |
254,5 |
|
95,64 |
75,54 |
95,64 > 75,54 |
|
|
|
|
|
|
|
|
|
|
Вывод: трещиностойкость всех расчетных сечений стенки |
обеспечена. |
||||||
3.3.3. Конструкция стенки резервуара и стеновой панели
Конструкция и принцип армирования стенки резервуара при использовании стержневой предварительно напрягаемой арматуры сохраняется такой же, как и при применении проволочной арматуры. Требования к расстоянию между стержнями остаются такими же, как и для проволочной арматуры.
Армирование стенки резервуара предварительно напрягаемой стержневой арматурой показано на рис. 27.
Конструкция и принцип армирования стеновой панели при использовании стержневой напрягаемой арматуры сохраняется такой же, как и при применении проволочной арматуры (см. рис. 21).
4.ШАРНИРНО-ПОДВИЖНОЕ СОЕДИНЕНИЕ СТЕНКИ
СДНИЩЕМ
4.1.Расчетные усилия, действующие в стенке резервуара
При шарнирно-подвижном соединении стенки с днищем в основании стенки возникают силы трения (рис. 28).
Величина их определяется по формуле
Qтр N f , |
(4.1) |
где N – нормальная сила; f коэффициент трения стенки о днище.
Сила трения определяется для двух расчетных случаев.
1. Резервуар не засыпан грунтом (случай при гидравлическом испытании резервуара).
В этом случае в стенке резервуара от гидравлического давления воды возникают кольцевые растягивающие усилия, величина которых определяется по формуле
|
N |
k |
N |
от 2 т r Q |
, |
(4.2) |
|
||
|
|
|
k |
тр |
|
1 |
|
|
|
где Nот |
кольцевое усилие |
без учета |
связи |
стенки с |
днищем; r – радиус резервуара; т, |
параметры, |
|||
k |
|
|
|
|
|
|
|
1 |
|
определяемые так же, как и для жесткого соединения стенки с днищем (подраздел 3.1.1).
При определении силы трения Qтр необходимо учитывать выполнение условия
43

Q |
|
Pmax |
, |
(4.3) |
|
||||
тр |
|
2 т |
|
|
где Рmax – гидростатическое давление у низа стенки.
Указанное ограничение для сил трения объясняется следующими соображениями. При Qтр Pmax – кольцевое
2 т
растягивающее усилие на уровне днища Nk |
= 0 [вытекает из формулы (4.2)]. При Q |
|
Pmax |
кольцевое усилие |
|
||||
|
тр |
|
2 т |
|
меняет знак. Вместо растяжения – сжатие, что теряет физический смысл.
2. Резервуар засыпан грунтом (случай при эксплуатации резервуара).
От давления грунта в стенке резервуара возникают кольцевые сжимающие усилия. Эти усилия обычно в расчете не учитываются, так как в резервуаре, заполненном водой, они уменьшают величину кольцевых растягивающих усилий, а в опорожненном резервуаре воспринимаются бетонным сечением стенки. При определении усилий в стенке резервуара от давления грунта следует иметь в виду, что в резервуаре, не заполненном жидкостью, возникают изгибающие моменты в меридиональной плоскости.
Величина их определяется по формуле
M |
Qтр |
|
. |
(4.4) |
|
т |
|||||
|
2 |
|
|
Обращаем внимание, что максимальный изгибающий момент будет действовать в том сечении, где коэффициент
2 (см. табл.1) будет иметь наибольшее значение.
Пример. Определение расчетных усилий, действующих в стенке резервуара.
Случай 1. Резервуар не засыпан грунтом.
А. Определение сил трения.
Расчет выполним для резервуара, конструкция которого показана на рис. 10. Нормальные силы определяются от веса покрытия и стенки.
1. Вес покрытия.
Покрытие резервуара выполнено из квадратных в плане панелей размером 4,5x4,5 м. Панель окаймлена по контуру ребрами и опирается непосредственно на колонны.
Толщина плиты 10 см.
Высота ребер 40 см.
Ширина ребер:
на уровне низа плиты 20 см;
по низу 15 см.
а) Нагрузка от веса железобетонных панелей на 1 м2:
|
|
0,20 0,15 |
|
|
|
|
|
|
1,1 0,1 4,5 4,5 4 0,4 |
0,1 |
|
4,5 |
2500 |
|
|
||
2 |
|
|
||||||
|
|
|
|
|
|
402 кгс/м2. |
||
|
4,5 4,5 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
f 1,1. |
|
|
|
|
|
|
|
|
б) Цементная стяжка: 0,025 2200 1,3 71,5 72 |
кгс/м2; |
f |
1,3. |
|||||
в) Гидроизоляционный ковер: 10 1,3 13 кгс/м2; |
|
f 1,3. |
|
|||||
Расчетная равномерно распределенная нагрузка по площади покрытия: 402 + 72 + 13 = 487 кгс/м2 .
44

Давление на 1 пог.м основания стенки от веса покрытия: 487 4,5 1096 кгс/пог.м = 1,096 тс/пог.м .
2
2. Нагрузка от веса стенки: 1,1 0,16 4,8 2500 2112 кгс/пог.м; |
f |
1,1. |
3.Нагрузка от веса торкретной штукатурки:
наружной – 40 мм (вариант стержневой арматуры);
внутренней – 20 мм.
1,3 0,04 0,02 4,8 2200 824 кгс/пог.м; |
f |
1,3. |
Нагрузка от веса стенки с штукатуркой
2112 + 824 = 2936 кгс/пог.м = 2,936 тс/пог.м.
Нормальное усилие от веса покрытия и стенки
N1 Nпокр Ncт 1,096 2,936 4,032 4,03 тс/пог.м.
Сила трения
Qтр N1 f 4,03 0,5 2,02 тс/пог.м,
где f =0,5 – при заполнении шва битумной мастикой.
Проверяем условие
Qтр Pmax .
2 т
Рmax=5,28 тс/м (см. табл.2).
т =1,08 (см. подраздел 3.1.1).
|
|
|
|
|
|
|
|
|
|
|
Pmax |
|
|
5,28 |
2,44 тс/м. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 т |
|
2 1,08 |
|
|
|
|
|||||
|
Qтр1 2,02 тс/м < 2,44 тс/м – условие удовлетворяется. |
|
|
|
|
|||||||||||||||||
Б. Определение кольцевых растягивающих усилий. |
|
|
|
|
|
|
|
|
||||||||||||||
|
Кольцевые растягивающие усилия с учетом сил трения определяем по формуле (4.2): |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
N |
k |
N |
от 2 т r Q . |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
тр |
1 |
||||||
|
Разбивку стенки на зоны сохраняем такой же, как и при жестком защемлении (см. рис.14). Для каждой зоны |
|||||||||||||||||||||
определяем усилия. Вычисление усилий сводим в табл.10. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 10 |
|
|
|
|
|
|
|
|
Кольцевые растягивающие усилия с учетом сил трения |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Номерсечения |
|
h |
стенки), м |
от(хниза |
стенки), м |
Nk , |
|
|
|
2 т r Qтр 1 |
|
N |
|
|
||||||||
|
т |
х |
|
|
тс/м |
|
|
|
|
|
|
|
|
|||||||||
|
|
верха |
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
||||
|
|
|
|
|
|
от |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(от |
|
|
|
тс |
|
|
1 |
Qтр1 |
2,02 |
тс |
|
кН |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
І |
|
|
0,4 |
|
4,4 |
3,96 |
4,75 |
|
0,003 |
0,012 |
|
3,95 |
|
38,75 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ІІ |
|
|
1,3 |
|
3,5 |
12,87 |
3,78 |
|
-0,0177 |
-0,695 |
|
|
13,57 |
|
133,12 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ІІІ |
|
|
2,3 |
|
2,5 |
22,77 |
2,70 |
|
-0,0608 |
-2,388 |
|
|
25,16 |
|
246,82 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ІV |
|
|
3,3 |
|
1,5 |
32,67 |
1,62 |
|
-0,0059 |
-0,232 |
|
|
32,90 |
|
322,75 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
V |
|
|
4,3 |
|
0,5 |
42,67 |
0,54 |
|
0,4927 |
19,348 |
|
|
23,32 |
|
228,77 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
VI |
|
|
4,8 |
|
0,0 |
47,52 |
0,00 |
|
1,0000 |
39,269 |
|
|
8,25 |
|
80,93 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Случай 2. Резервуар засыпан грунтом.
45

А. Определение сил трения.
При определении величины нормальной силы для этого случая необходимо к нагрузке N1 (случай 1)
дополнительно добавить нагрузку, находящуюся на покрытии (вес засыпки грунтом, временную нагрузку).
Пример.
Нормальное усилие – случай 1.
N1= 4,03 тс/пог.м.
Вес от засыпки грунтом: |
|
1,15 1,0 1700 1955кгс/м2; |
f 1,15. |
Расчетная временная равномерно распределенная нагрузка: |
|
1,4 2800 3920 кгс/м2; |
f 1,4. |
Итого: 1955 + 3920 = 5875 кгс/м2. |
|
Давление на 1 пог.м основания стенки |
|
5875 4,5 13219 кгс/пог.м = 13,22 тс/пог.м.
2
Полное нормальное усилие
N2 = 4,03 + 13,22 = 17,25 тс/пог.м.
Сила трения
Qтр 17,25 0,5 8,63 тс/пог.м.
Б. Определение изгибающих моментов, действующих в вертикальной плоскости стенки.
Меридиональный максимальный изгибающий момент в стенке резервуара определяется по формуле (4.4).
M |
Qтр |
|
2max . |
|
|||
|
т |
|
|
Согласно табл. 1 |
|
||
2max 0,3223; |
0,8. |
||
Тогда |
|
||
х 0,8 0,74м ( от низа стенки).
т1,08
Величина максимального изгибающего момента равна
M8,63 0,3223 2,58 тc пог.м. 1,08
Обращаем внимание, что местоположение сечения по высоте стенки резервуара, в котором действует наибольший изгибающий момент, может быть определено и по эмпирической формуле
х 0,6 
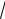 r 0,6
r 0,6 
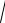 9 0,16 0,72м.
9 0,16 0,72м.
Меридиональный изгибающий момент учитывается при расчете площади сечения вертикальной арматуры стенки резервуара. Дальнейший расчет резервуара выполняется аналогично расчету для варианта жесткого соединения стенки с днищем.
Библиографический список
1.Байков В.Н. Железобетонные конструкции. Общий курс/В.Н. Байков. – М.: Стройиздат, 1991. 2.Бондаренко В.М. Железобетонные и каменные конструкции/В.М. Бондаренко. – М.: Высшая школа, 2002.
46
3.Величкин А.П. Справочник проектировщика инженерных сооружений/А.П. Величкин. – Киев: Будивельник, 1973.
4.СНиП 2.03.01-84*. Бетонные и железобетонные конструкции. Нормы проектирования. – М., 1989. 5. СНиП 2.01.07-85. Нагрузки и воздействия. – М., 1985.
6.Сычев В.И. Унификация железобетонных инженерных сооружений/В.И. Сычев. – М.: Стройиздат, 1971.
47
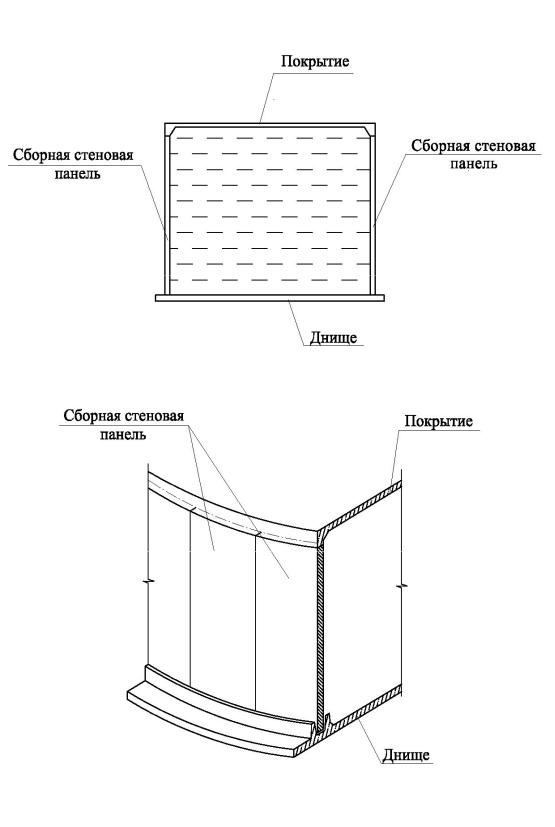
Рис. 1. Цилиндрический железобетонный резервуар
48
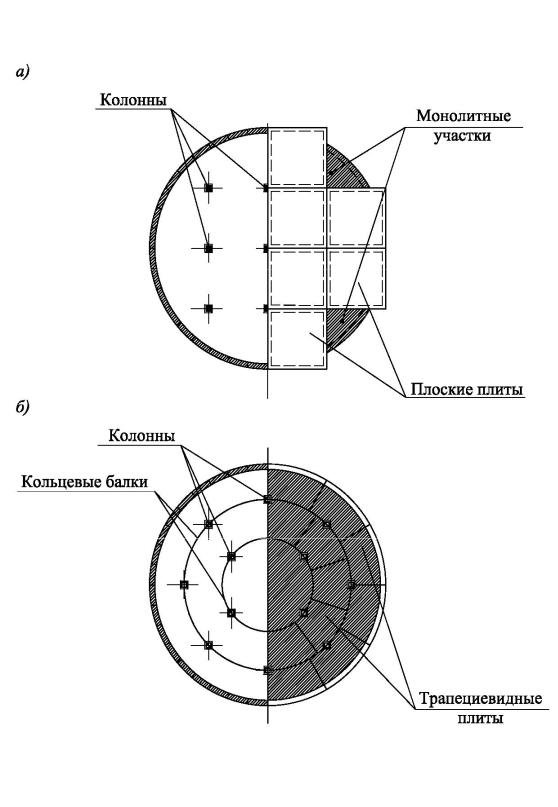
Рис. 2.Типы сборных покрытий цилиндрических резервуаров:
а покрытие из плоских плит; б покрытие из трапециевидных плит
49
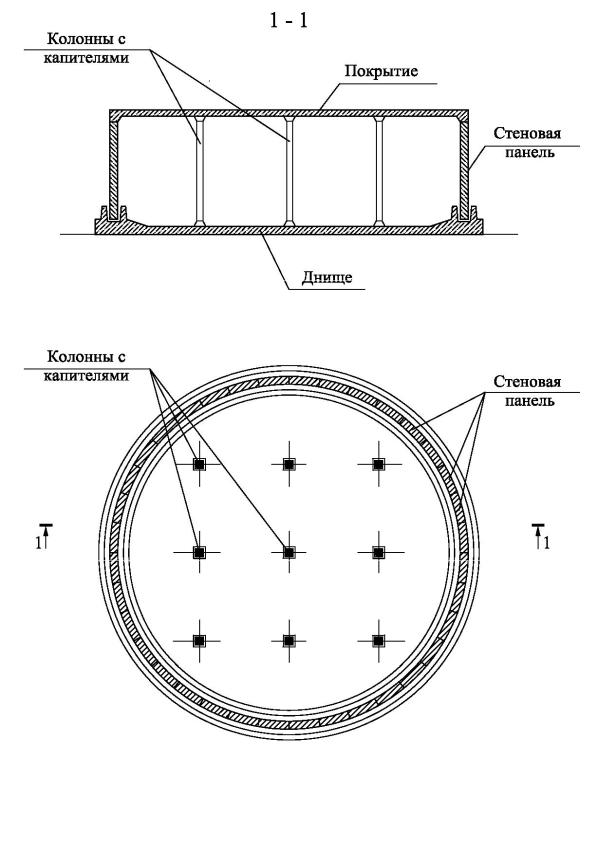
Рис.3. Цилиндрический резервуар с безбалочным перекрытием
50
