Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1903.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

2.14 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

Министерство образования и науки РФ Федеральное государственное бюджетное образовательное

учреждение высшего образования «Сибирская государственная автомобильно-дорожная академия

(СибАДИ)»

Кафедра «Геодезия»

ИНЖЕНЕРНАЯ ГРАФИКА И ТОПОГРАФИЧЕСКОЕ ЧЕРЧЕНИЕ

СибАДИМетодические указания

к практическим занятиям

Состав тели: О.М. Третьяк, Е.А. Курышева

Омск  2016

Согласно 436-ФЗ от 29.12.2010 «О защите детей от информации, причиняющей вред их здоровью и развитию» данная продукция маркировке неподлежит.

УДК 515

ББК 22.151.34 И62

Рецензент канд. техн. наук, доц. А.Г. Малофеев (СибАДИ)

Работаутвержденаредакционно-издательскимсоветомСибАДИвкачествеметодических указаний.


И62	Инженерная графика и топографическое черчение [Электронный ресурс] :
методические указания к практическим занятиям / сост. : О.М. Третьяк,		Е.А.

Курышева. – ЭлектронСибАДИ. дан. − Омск : СибАДИ, 2016. – URL: http://bek.sibadi.org/cgibin/irbis64r_plus/cgiirbis 64 ft.exe. - Режим доступа: для авторизованных пользователей.

Излагается методика выполнения практических работ обучающимися по дисциплине «Инженерная графика и топографическое черчение».

Имеют интерактивноеоглавление в виде закладок.

Предназначены для обучающихся направления «Геодезия и дистанционное зондирование»профиль«Геодезия».

Текстовое (с мвольное) издание (2,0 МБ)

Системные требования : Intel, 3,4 GHz ; 150 МБ ; Windows XP/Vista/7 ; DVD-ROM ; 1 ГБ свободного места на жестком диске ; программа для чтения pdf-файлов

Adobe Acrobat Reader ; Google Chrome

Редактор И.Г. Кузнецова Техническая подготовка Т.И. Кукина

Издание первое. Дата подписания к использованию 28.10.2016

Издательско-полиграфический центр СибАДИ. 644080, г. Омск, пр. Мира, 5 РИО ИПЦ СибАДИ. 644080, г. Омск, ул. 2-я Поселковая, 1

ВВЕДЕНИЕ

Инженерная графика включает в себя основы начертательной геометрии и основы специального вида технического черчения.

Начертательная геометрия – наука, изучающая закономерности изображения пространственных форм на плоскости и решения пространственных задач проекционно-графическими методами.

Метод проекций с числовыми отметками является разделом курса начертательной геометрии и чаще всего применяется при составлении чертежей строительных объектов, у которых размеры по высоте значительно меньше размеров по ширине и длине. Решение задач в проекциях с числовыми отметками в итоге сводится к разработке чертежей с вертикальной планировкой для таких сооружений, как пересечение автомобильных дорог в одном или двух уровнях, подходы к мостовым переходам, автобусные остановки и т.д. Чертежи в проекциях с числовыми отметками дают представление не только о форме сооружения и его размерах, но и об уклонах, о направле-

нии стока паводковых и ливневых вод, об объёмах земляных работ.
	И
Картограмма земляных работ составляется по чертежам в проекциях с
числовыми отметками.	Д

Рассматриваются понятия проекций с числовыми отметками

точки, прямой, плоскости, поверхностиА, их взаимного расположения, пример решения нженерной задачи, перечень вопросов и условий задач для самопроверки.

иб 1. ПРОЕКЦИИ ТОЧКИ, ПРЯМОЙ, ПЛОСКОСТИ

ПоложениеСв пространстве любой точки, изображенной в проекциях с числовыми отметками, определяется двумя параметрами: ее прямоугольной проекцией на горизонтальную плоскость П0 (плоскость нулевого уровня) и высотной отметкой точки, которая указывается в виде индекса в обозначении точки.

Отметка точки – это расстояние от изображаемой точки до плоскости нулевого уровня. За единицу измерения обычно берут 1 м. Отметка точки может быть положительной и отрицательной.

Чертеж, выполненный в проекциях с числовыми отметками, принято называть планом и сопровождать численным и линейным масштабами. На рис. 1, а дано наглядное изображение расположения точек А, В, С, D в пространстве; на рис. 1, б – чертеж этих точек в

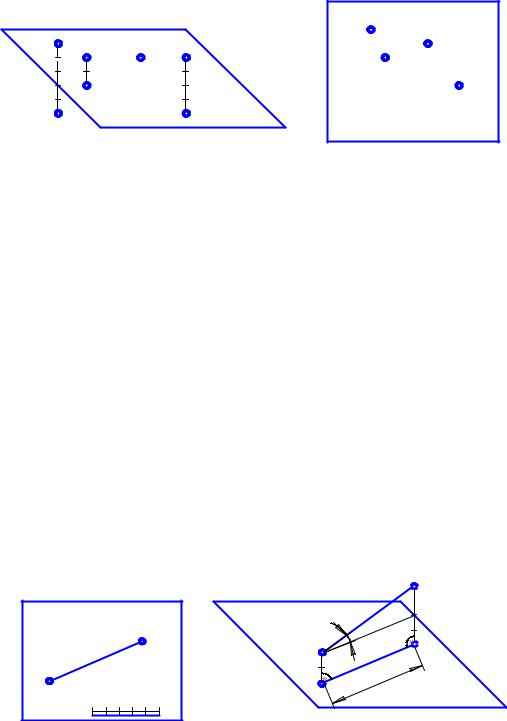
проекциях с числовыми отметками. Если соединить две из имеющихся точек прямой линией, то получим чертеж прямой линии в проекциях с числовыми отметками (рис. 2, а).

a )	а
a )
D-5	B C=C0 A
D	B2	A4
D		A4

б )	б
D-5		C0
	B2	A4
		A4

-2 -1 0 1 2 3 м

М 1 : 200

Рис. 1. Наглядное изображение расположения точек в пространстве (а) и чертеж этих точек в проекциях с числовыми отметками (б)

Длину проекции прямой на горизонтальную плоскость (В2 А4)
называют заложением. Заложение обозначают буквой L (рис. 2, б).
Разность высот точек A и B называют превышениемИ∆h.
∆h = hA – hB.
			Д
Отношение превышения к заложению называют уклоном пря-
мой и обозначают буквой i.		А
б
и	i = Δh / L.
		AB к горизонтальной плоскости		П0	яв-
Углом наклона φ прямой

ляется острыйСугол между прямой и её проекцией на плоскость П0

(см. рис. 2, б).

а )	а	б ) б




			B
	A4		B
	A4			L
B2		B2		L
		B2
	-2 -1 0 1 2 3 м

П 0

Рис. 2. Проекция линий

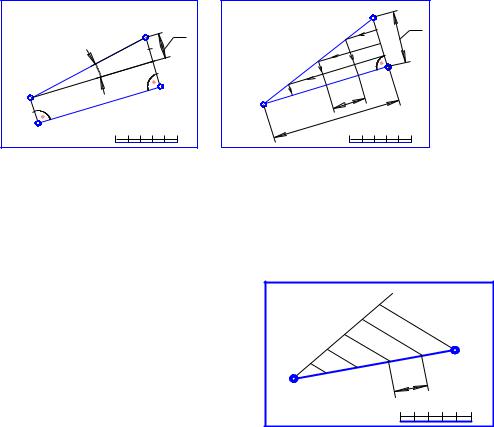
На рис. 3 показано определение натуральной величины отрезков AB и AC как гипотенузы прямоугольного треугольника, одним катетом которого является заложение L, а другим превышение конечных точек отрезка ∆h. На этом же рисунке показано градуирование прямой AC, т.е. определение на заложении прямой положения точек, имеющих отметки, кратные 1 м. Если градуирование прямой выполняется на чертеже, где отсутствует натуральная величина, то используют произвольную прямую KE, на которой отмеряют необходимое количество произвольных, но равных между собой отрезков (рис. 4).

а )

б )

A 4

C= C0

B 2

-2 -1 0 1 2 3 м

Рис. 3. Определение натуральной величины отрезков

Если превышение прямой равно единице, то заложение такого

отрезка называют

нтервалом. Интервал – это горизонтальная проек-

ция отрезка, разность отметок концов

которого равна 1 м. Интервал обозна-

чают буквой (см. риси. 3, 4). Интервал

и уклон величины обратно пропор-

N 7

циональные.

К 2

-2 -1 0 1 2 3 м

i = 1/ ; = 1/i.

Рис. 4. Градуирование прямой

Плоскость может быть задана на проекциях с числовыми отметками различными способами (рис. 5):

‒ параллельными прямыми (рис. 5, а). Признаками параллельности прямых на проекциях с числовыми отметками являются параллельность проекций, равенство интервалов и одинаковое направление уклонов;

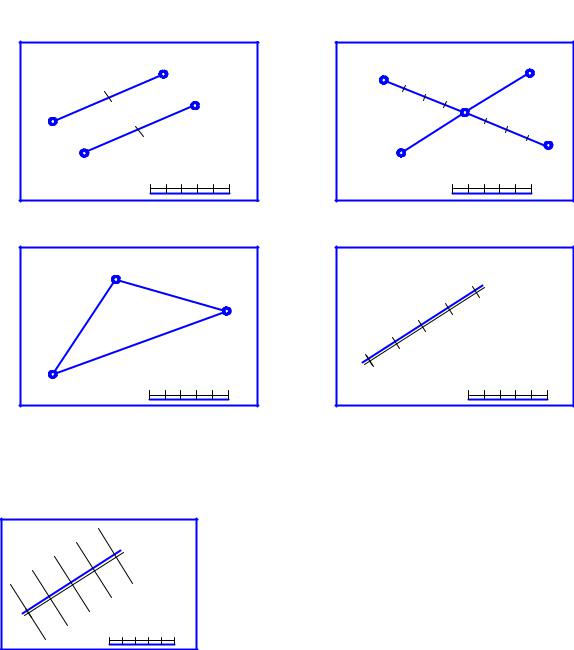
‒пересекающимися прямыми (рис. 5, б). Признаком пересечения двух прямых на проекциях с числовыми отметками является наличие общей точки K, которая имеет одинаковую отметку для каждой из двух прямых;

‒тремя точками или любым плоским n-угольником (рис. 5, в);

‒проекцией на горизонтальную плоскость проградуированной линии ската, которая называется масштабом уклона (рис. 5, г). Масштаб уклона принято изображать двумя параллельными линиями (основной и тонкой).

а )

б )

C-2 -1

-2 -1 0 1 2 3 м

в )

г }г

-2 -1 0 1 2 3 м

Рис. 5. Задание плоскости на проекциях с числовыми отметками различными

способами

Известно, что линия ската перпенди-

кулярна

горизонталям

плоскости.

Таким

образом,

согласно теореме

проекциях

прямого угла, угол между масштабом ук-

лона и

проекциями

горизонталей

будет

-2 -1

0 1 2 3 м

прямой (рис. 6).

Рис. 6. Линия ската

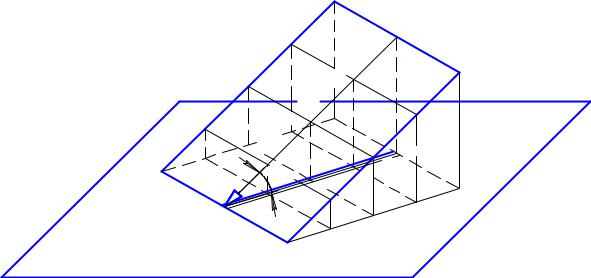
Угол φ между линией ската и масштабом уклона является углом наклона плоскости к плоскости нулевого уровня П0 (рис. 7).

		4
	3
	2		т	а	a	4
		а			a	4


	к
	с				3
1	я
1	и
	н
	и				4
0	Л				2
0				3	2

		2
	1	2
	1		1
			1
	0				И
П 0	0				И
П 0	0	Д
		Д

Рис. 7. Угол наклона плоскости к плоскости нулевого уровня П0

2. ВЗАИМНОЕ Р СПОЛОЖЕНИЕ ДВУХ
ПЛОСКОСТЕЙ, ПРЯМОЙ И ПЛОСКОСТИ
	б
Многие положения относительно взаимного расположения двух
и
плоскостей или прямой	плоскостиА, изображенных в ортогональных
проекциях, примен мы	к проекциям с числовыми отметками.
С

Прямая лин я леж т в плоскости, если имеются две точки, общие для прямой и плоскости.

Точка принадлежит плоскости, если она расположена на какойлибо прямой этой плоскости.

Если две плоскости параллельны (рис. 8), то в проекциях с числовыми отметками:

‒масштабы уклонов их параллельны;

‒интервалы равны;

‒отметки возрастают в одну сторону.

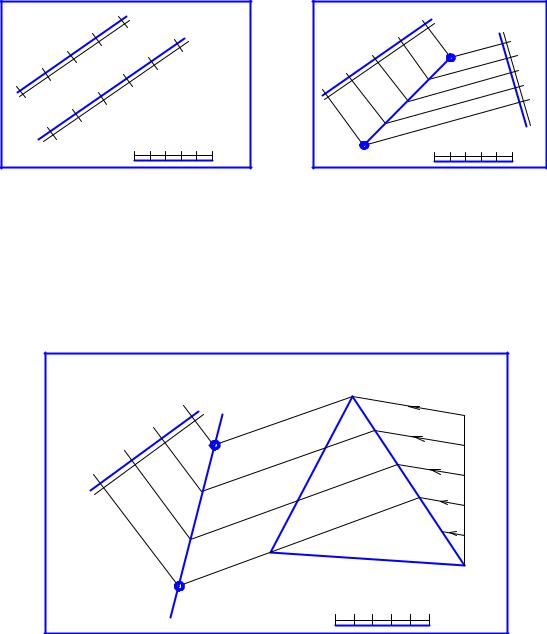
Если две плоскости пересекаются (рис. 9), то достаточно определить две точки K и N, общие для этих плоскостей. В проекциях с числовыми отметками эти точки определяются как точки пересечения горизонталей одного уровня.

	ai	bi
	6	bi
	5	9
	4	9
	4	8
3	7	8
3	7
2	6
	6
4	5
4	-2 -1 0 1 2 3 м
Рис. 8. Плоскости параллельны

		ai	bi
	6	K6	6
	5		5
	4		4
	4		3
	3		3
2	3		2
2
N2	-2 -1 0 1 2 3 м
Рис. 9. Плоскости пересекаются

Если одна или обе пересекающиеся плоскости заданы другими
способами (см. рис. 5, а, б, в), то положение одноименных горизонта-
лей определяется после градуирования прямых линий, задающих
плоскость (рис. 10). В данном случае выполнено градуирование пря-
мой АС.
							A7
					K7		И
				7	K7	Д		7 0
			6			Д		6 0
		5			А			6 0
		5						5 0
	4							5 0
ai	4							4 0

				б
				б			b	3 0
		и B4					b	3 0
		и B4						C2
	С			N4			-2 -1 0 1 2 3 м
	С
		Рис. 10. Градуирования прямых линий

На рис. 11 показано определение точки пересечения прямой АВ с плоскостью α. При этом выполняют те же вспомогательные построения, что и при решении данной задачи в ортогональных проекциях:

‒ через прямую AB проводят вспомогательную плоскость β. Задают ее параллельными горизонталями соответствующего уровня. Направление горизонталей выбирают произвольно;

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.2021202.83 Кб019.pdf
#
07.01.2021337.37 Кб3190.pdf
#
07.01.20212.13 Mб201900.pdf
#
07.01.20212.13 Mб21901.pdf
#
07.01.20212.14 Mб61902.pdf
#
07.01.20212.14 Mб21903.pdf
#
07.01.20212.16 Mб1271905.pdf
#
07.01.20212.16 Mб71906.pdf
#
07.01.20212.16 Mб51907.pdf
#
07.01.20212.17 Mб51908.pdf
#
07.01.20212.17 Mб21909.pdf