Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1835

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.94 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

x cos ;

имеем параметрическое

В силу формул перехода

y sin

задание дуги AB:

x ( )cos ;

y ( )sin ,

По формуле (5)

LAB

cos sin

sin cos

d 2

2d .

LAB

(7)

Пример.

Вычислить длину кардиоиды a(1 cos ) (рис. 6).

L 2

d	2
			asin 2 a2(1 cos )2d
		2d 2


d		0


2a	2 2cos d 4a cos			d 8a				8a.
					sin
			2		sin	2
0	0		2			2	0
		y
		a		a 1 cos
								2a
		0						x

-a

Рис. 6

Лекция №11. ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА (ВЫЧИСЛЕНИЕ

ОБЪЕМОВ И ПЛОЩАДЕЙ ПОВЕРХНОСТЕЙ). ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ

Пусть задано пространственное тело, заключенное между плоскостями x a и x b, и известны площади поперечных сечений этого тела, т. е. при фиксированном x0 a,b плоскость x x0 высекает сечение площадью S S(x0) (рис. 1).

y x a

x b

S x

0 a

x dx

b x

Рис. 1

Берем произвольный отрезок соответствует слой тела объемом объема тела принимаем объем высотой dx.

x,x dx a,b . Этому отрезкуV , за приближенное значение цилиндра с основанием S(x) и

b
V dV S(x)dx V S(x)dx.
a
b
V S(x)dx.	(1)
a

Из формулы (1) легко получить формулу для вычисления объема тела вращения.

Вращаем криволинейную трапецию вокруг оси Ox. Плоскость x x0 оси Ox, пересекает тело, причем в сечении – круг (рис. 2).

	S R2 f (x) 2 .
b	b

V f (x) 2dx или V y 2dx.

y f x	B
A

0 a			x0			b x
z
		Рис. 2
				b
Если вращаем вокруг оси Oy V x 2dy,							x f 1(y).
Примеры.				a
Примеры.		2	y2		2
1. Найти объем эллипсоида	x	2	y2	z	2	1 (рис. 3).
1. Найти объем эллипсоида	a	2	b2	c	2	1 (рис. 3).
	a	2	b2	c	2

Сечения эллипсоида координатными плоскостями:

	z		0;
1)			2	y	2
		x		y		1
				b2		1
	a2			b2
	y 0;
2)			2	z	2
		x		z		1
				c2		1
	a2			c2
	x 0;
3)			2	z	2
		y		z		1
				c2		1
	b2			c2

–эллипс с осями 2a и 2b .

–эллипс с осями 2a и 2с.

–эллипс с осями 2b и 2с.

V S(x)dx.

	~		~2	y	2	z	2
	~		x	y		z
В сечении плоскостью x	x	имеем эллипс						1.
В сечении плоскостью x	x	имеем эллипс	a2	b2		c2		1.
	z	с
		с
		- a
		b y
a
x		- с
		Рис. 3

–

полуоси

эллипса.

S(x) bc bc 1

dx bc x

abc.

3 3

элл

abc .

Если a b c R(сфера), то V

сф

R3.

2. Найти объем тела, полученного от вращения волны

синусоиды (рис. 4).

1 cos2x

Vт.вр y

2dx sin2

xdx

sin2x

y sin x

Рис. 4

Площадь поверхности вращения

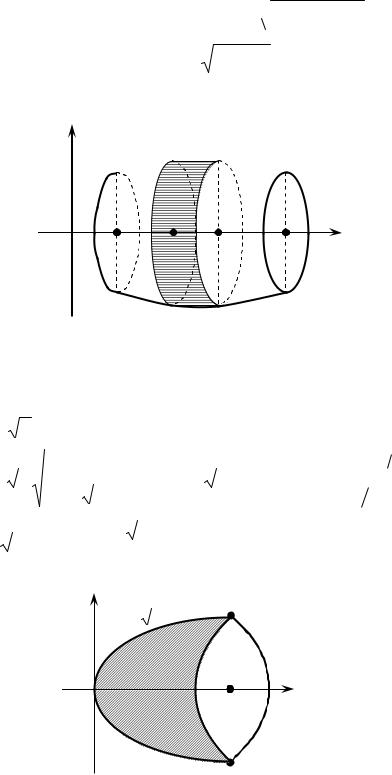
AB (y f (x)) вращается вокруг оси Ox (рис. 5).

x,x dx кольцо площадью . За приближенное значениевозьмем площадь цилиндрического кольца, в основании которого окружность R f (x). Высота dS – дифференциал длины дуги AB , т.е.

d 2 R dS 2 f (x)1 f (x) 2dx.

b	1 y 2dx.
2 y	1 y 2dx.	(2)

y f x

A B

x x dx

Рис. 5

Пример.

Найти площадь поверхности тела, полученного от вращения

параболы y 2				x	вокруг оси Ox , 0 x 1 (рис. 6).
																	(x 1)3 2 1
	1							1			2		1
	1							1					1
2 2 x					1						dx 4					x 1dx 4
																		3 2

	0								x				0						0
	2					2		8 2						1
												2
												2
4		2	2												15,3 кв.ед.
4	3	2	2								3				15,3 кв.ед.
	3					3					3
							y
										y 2
										y 2				x

Рис. 6

Физические приложения определенного интеграла

К определенным интегралам приводят многочисленные задачи естествознания.

1. Задача о пройденном пути (см. лекцию №6).

S lim v i ti v(t)dt.

0 i 1

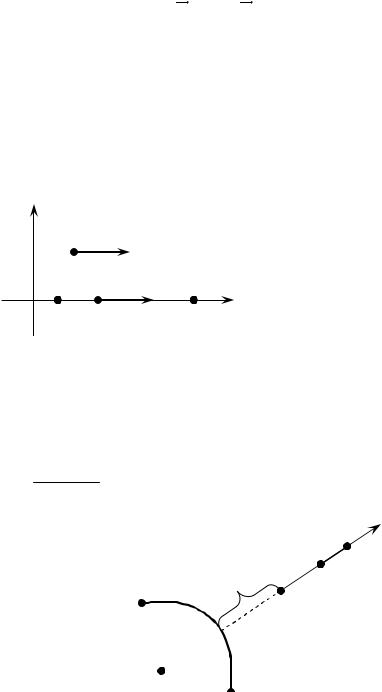
2.Задача о работе переменной силы.

Пусть материальная точка под действием переменной силы переместилась прямолинейно от положения x a в положение x b (рис. 7).

		df
		df
	F	F(x)	,
F \|\|Ox,	F	F(x)	,

x,x dx A dA F(x)dx.

F x

A F(x)dx.

0 a

x dx b x

Рис. 7

Пример.

Какую работу надо произвести, чтобы 1 кг массы поднять с поверхности Земли за пределы земного тяготения (рис. 8)?

F(h) h R 2 – сила притяжения 1 кг массы.

A x

h+dh

На уровне моря h 0, F(0) 10 с R2 10,

h,h dh A dA F(h)dh .

10R

dh lim 10 R2 h R 2dh

H r 2

R2 A

R 10 6,4 107.

lim 10

lim 10 R

h R 0

B R

3. Задача о давлении жидкости на площадки различных профилей.

x,x dx площадка шириной dx (рис. 9). Давление на эту площадку

Уровень жидкости

0 y

x dx

b	y f x	y x
x	y f x	y x
	Рис. 9
P dP g x ABdx, где – плотность, кг/м3; g – ускорение
свободного падения, м/с2;	AB (x) f (x).

dP g x( (x) f (x))dx P g x( (x) f (x))dx.

Пример.

Найти давление воды на прямоугольную пластину размером

a b.


x,x dx dP gbdx x,				1.
a	x2	a	5a2b кН.
P 10 bx dx 10b
P 10 bx dx 10b
0	2	0

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Лекция №12. ОПРЕДЕЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ, ПРЕДЕЛ, НЕПРЕРЫВНОСТЬ

Функция одного действительного переменного не исчерпывает всех зависимостей между величинами. Так, площадь прямоугольника S x y есть функция двух переменных, температура в данной части

пространства есть функция трех координат точки (x, y,z)			и времени
		v	2 sin2
t, т.е. T f (x, y,z,t), дальность полета снаряда	S		0	–

функция начальной скорости v0, угла наклона ствола орудия φ и ускорения свободного падения g и т.д. Дадим определение функции нескольких переменных с точки зрения современной математики.

Определение. Пусть даны два произвольных множества E и F. Говорят, что задано отображение множества E во множество F, если указано правило, по которому каждому элементу множества E ставится в соответствие элемент множества F.

Отображение множества E во множество F называется также функцией, определенной на множестве E со значениями во множестве

При этом пишут f : E F , или f : x E y F , или y f (x). Множество E называют областью определения функции, множество F – областью значений.

С позиции этого определения:

1. Функция одного действительного переменного – это отображение множества действительных чисел R (или любого его подмножества) опять в R.

f : x R y R. y f (x).

2. Функция двух действительных переменных – это отображение плоскости xOy (или любой ее области) R2 во множество действительных чисел R.

f : M R2 z R.

z	f (M) или	z f (x, y).
3.	Функция	трех действительных переменных – это

отображение пространства Oxyz (или любой области пространства) R3 во множество действительных чисел R.

f : M R3 u R.

u f (M) или u f (x, y,z).

Определение. Функцией n действительных переменных будем называть отображение n – мерного Евклидова пространства Rn (или любой области этого пространства) на множество действительных чисел R.

f : M Rn R.

Введем в Евклидовом пространстве понятие n – мерной сферы и ε окрестности точки.

Определение. n – мерной сферой Евклидова пространства Rn с

центром в точке M0 x10,x20, ,xn0 и радиусом r называют множество точек M x1,x2, ,xn , удовлетворяющих уравнению

x0 2

r2.

(1)

0, ,x0

Определение. ε

окрестностью

точки

будем

называть открытый n – мерный шар с центром в точке M0

и радиусом

ε, т.е. множество точек

M x1,x2, ,xn ,

удовлетворяющих

неравенству

x0 2 x

2 x

x0 2

(2)

В случае R2 (т.е. плоскости xOy) ε окрестность точки

–

открытый круг радиуса ε, в

случае

(пространства Oxyz)

–

открытый шар радиуса ε .

Предел и непрерывность

Определение. Число A называется пределом функции u f (M)

в т.

M0, если для 0, 0, что как только

0 (M,M0) ,

так

f (M) A

и пишут

lim

f (M) A.

M M0

Здесь

(M,M

)

x x0 2

x0 2

–

расстояние между M и M0.

f (x, y) A, т.к.

В случае двух переменных

lim

для

x x0

y y0

что из

x x0 2 y y0 2

f (x, y) A

Геометрический смысл предела заключается в том, что как

только т.M попадает в δ окрестность т. M0,

так значения функции в

этой точке попадают в ε окрестность точки A .

Определение. Функция u f (M)

называется непрерывной в т.

M0, если M0

входит в область определения функции и

lim

f (M) f (M0).

(3).

M M0

f (x, y) f (x0, y0).

В случае двух переменных

lim

x x0

y y0

Если функция непрерывна в каждой точке области G , то ее называют непрерывной в области G .

Для непрерывных функций имеют место свойства, аналогичные свойствам непрерывных функций одного переменного.

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.92 Mб11830.pdf
#
07.01.20211.93 Mб21831.pdf
#
07.01.20211.93 Mб221832.pdf
#
07.01.20211.93 Mб51833.pdf
#
07.01.20211.93 Mб951834.pdf
#
07.01.20211.94 Mб21835.pdf
#
07.01.20211.94 Mб21836.pdf
#
07.01.20211.94 Mб41837.pdf
#
07.01.20211.95 Mб251838.pdf
#
07.01.20211.95 Mб01839.pdf
#
07.01.2021333.77 Кб7184.pdf