Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирская государственная автомобильно-дорожная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1835

.pdf

Скачиваний:

Добавлен:

07.01.2021

Размер:

1.94 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

КАНОНИЧЕСКОЕ РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ. РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ РАЗЛОЖЕНИЕ

Определение. Многочленом n-й степени называется функция

вида P(x) a		0	xn	a xn 1 ... a			n 1			x a			n	, где a R, n N .
		0		1			n 1						n				i
Определение. Число						R					или					С называется корнем
многочлена P(x), если P( ) 0.
Проще всего находятся корни квадратного трёхчлена.
1) P(x) ax2 bx c – общего вида.
								b
					x			b				b2 4ac						.
					x													.
				1,2							2a
2) P(x) x2											2a
2) P(x) x2				px q – приведённого вида.

									p					p		2
					x1,2											q .
					x1,2				2							q .
									2					2
Зная эти корни, легко разложить многочлен на множители:
				ax2 bx c a(x x )(x x													2	).
Примеры:													1				2
Примеры:
1. 2x2 x 1 P(x).
x	1				1 3
	1			1 8	1 3	; x 1; x									2	2.
						; x 1; x										2.
1,2			4	4					1
			4	4

2x2 x 1 2(x 1)(x 1) (x 1)(2x 1). 2

2. x2 2x 10 P(x).

x 1	1 10	1	9	1 3i x2	2x 10
1,2
(x 1 3i)(x 1 3i).

Вслучае многочлена n й степени дело обстоит сложнее.

Те о р е м а Гаусса (основная теорема алгебры). Всякий многочлен n й степени имеет по крайней мере один корень, действительный или комплексный (без доказательства).

Те о р е м а Безу. Если число является корнем многочлена P(x), то многочлен делится без остатка на (x ).

Д о к а з а т е л ь с т в о

Пусть при делении P(x) на (x ) имеем частное Q(x) и остаток R. Q(x) – многочлен (n 1)-й степени, R – многочлен нулевой степени или число.

P(x) (x )Q(x) R.

Полагая x , имеем P( ) ( )Q( ) R

R P( ) 0 P(x) (x )Q(x), что и требовалось доказать. Из теоремы Гаусса и теоремы Безу следует, что многочлен n-й

степени имеет ровно n корней: 1, 2,..., n . Эти корни могут быть действительными или комплексными и могут совпадать. Через корни многочлен можно представить в виде произведения (теорема разложения).

Д о к а з а т е л ь с т в о

P(x) a0(x 1)Q1(x) a0(x 1)(x 2)Q2(x) ...
		a0(x 1)(x 2)...(x n ).							(1)
Т е о р е м а. Если комплексное число z a ib является
корнем многочлена		P(x), то и сопряжённое число						a ib	тоже
							z
корень этого многочлена.
		Д о к а з а т е л ь с т в о
Пусть P(x) a	0	xn a xn 1 ... a	n 1	x a	n	и P(z) 0.
		1

Рассмотрим P z a0 z n a1 z n 1 ... an 1 z an . В силу свойств сопряжённых чисел имеем

P z a0 z n a1 z n 1 ... an 1 z an

a	0	zn a zn 1	... a	n 1	z a	n		P(z)		0	0, что и требовалось
	0	1		n 1		n

доказать.

Доказанная теорема позволяет сгруппировать в разложении (1) множители с комплексно-сопряжёнными корнями. Если учесть, что

(x z)(x z) x2 (z z)x zz x2 2ax (a2 b2), то можно с учётом кратности корней представить разложение (1) в каноническом виде:

P(x) a0(x a) ...(x b) ...(x2	px q)t...(x2	rx s)h, (2)
где все коэффициенты R,	показатели	N , причём

... t ... h n, а все квадратные трёхчлены имеют D 0.

Примеры:

Найти каноническое разложение многочлена.

1.P(x) x4 1 (x2 1)(x2 1) (x 1)(x 1)(x2 1).

2.P(x) (x6 2x3 1) (x3 1)2 (x 1)2(x2 x 1).

Рациональные дроби. Разложение дробей на сумму простейших

Определение. Рациональной функцией, или рациональной дробью, называется функция вида

(x) P(x) , где P(x) и Q(x) – многочлены.

Q(x)

Если степень P(x) меньше степени Q(x) – дробь правильная, если больше – неправильная. Из всякой неправильной дроби можно выделить целую часть, поделив числитель на знаменатель.

Пример.

2x 1

2x 3

x2 2

x4 2x 1 | x2 2

x4 2x2

x2 2

17 |5

2x2

2x 1

Аналогично

15 3

2x2

2x 3

P(x)

Т е о р е м а.

Если дробь

правильная и знаменатель имеет

Q(x)

каноническое разложение, то есть (по теореме разложения)

Q(x) a0(x a) ...(x b) ...(x2 px q)t...(x2 rx s)h , то дробь можно представить в виде суммы следующих простых дробей:

P(x)

...

Q(x)

(x a)

x a

x b

Px Q

P x Q

Px Q

...

px q ...

(x b)

px q t

px q t 1

R1x 1

Rhx h

...

rx s .

rx s h

Здесь в числителях простейших дробей стоят неизвестные коэффициенты, которые определяются при помощи так называемого метода неопределённых коэффициентов. Этот метод уясним на примерах.

3x 1

2x 3

(x 3)(x 1)

x 3

x 1

(x2 2x 3 0 x

1 2 x 3; x

1).

1 3

1,2

3x 1

A(x 1) B(x 3)

3x 1 A(x 1) B(x 3).

x2 2x 3

(x 3)(x 1)

1-й способ.

A B 3;

(A B)x A 3B 3x 1

A 3B 1.

B 1, A 2.

2-й способ.

4B 4

A(x 1) B(x 3) 3x 1.

x 1 4B 3 1 B 1.

x 3 4A 8 A 2.

Итак,

3x 1

x 3

x2 2x 3

x 1

2x2

Cx D

(x 1)2 (x2

x2 1

(x 1)2

x 1

A(x2

1) B(x 1)(x2

1) (Cx D)(x 1)2

2x2

(B C)x3 (A B D 2C)x2 (B C 2D)x (A B D) 2x2 1.

D 0;

B C 0;

C B;

D 0;

;

A B D 2C 2;

A B D 2;

C B;

B C 2D 0;

2D 0;

A B 2;

;

A B D 1.

A B 1.

2x2 1

3 2

1 2

(x 1)2 (x2 1)

(x 1)2

x 1

x2 1

Лекция №5. ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ, ИРРАЦИОНАЛЬНЫХ И ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ

Теорема разложения рациональных дробей на простые даёт возможность свести множество различных интегралов от рациональных функций к четырём типам:

dx A

d(x b)

Aln

x b

C .

x b

(x b)1 k

dx A (x b) k d(x b) A

(x b)k

1 k

Ak 1(x b)k 1 C.

Mx N

dx, квадратный трёхчлен имеет дискриминант

px q

D 0.

p 2

px q

x p t x t p dx dt . 2 2

Mx N

tdt

dt M

px q

tdt

M ln t2

p 1

N M

arctg

t2 a2

2 a

ln x2 px q

2N Mp

arctg

2x p

3x 5

5 (x 1)

4 t

Пример.

2x 5

t x 1 x t 1 dx dt

3(t 1) 5

dt 3

tdt

d(t2 4)

dt 8

t2 4

2 4

4 2

ln t2 4 8

arctg

ln x2 2x 5 4arctg

x 1

IV.

Mx N

подстановкой t x

сводится к

px q k

интегралу

Ik . Применим метод интегрирования по частям:

2 a2

t2 a2 k

	u t2	a2 k

dv dt v t

	k 1			2kt
du k t2	a2	2tdt			dt
du k t2	a2	2tdt	t2	k 1	dt
			t2	a2

t2 a

2 a

t2 a2

t2 a2 k 1

t2 a2

2ka2

2 a2 k

t2 a2 k 1

В результате имеем Ik

2kIk

2ka2Ik 1.

a2 k

Ik 1

2k 1

Ik .

(1)

2ka

)

2ka

Формула (1) называется рекуррентным соотношением и позволяет последовательно вычислить все интегралы вида

, начиная с k 1.

t2 a2 k

1) I1

arctg

C .

2 a2

2a2 t2 a2

t2 a2 2

2a2

t2 a2

2a2 t2 a2

arctg

2a3

C и т. д.

4a2 t2

t2 a2

Из приведённых выше вычислений следует основная теорема. Т е о р е м а. Всякая рациональная дробь интегрируется в

элементарных функциях.

Пример.

				2x2 1									3 2										1 2 1 2x
										dx																	dx
(x 1)					2	(x	2			dx									2					x	2	1	dx
(x 1)						(x		1)					(x 1)									x 1		x		1
	3		x 1 2dx									1	dx				1				xdx
			x 1 2dx										x 1								x2 1
2								2					x 1		2						x2 1
		3		1				1	ln		x 1		1	ln		x		2		1			C .



			2 x 1
								2					4

Интегрирование иррациональных выражений

Определение. Функция, в аналитическом выражении которой над аргументами производится, наряду с арифметическими операциями, операция извлечения корня, называется иррациональной.

Примеры:

f (x)

3x2

– рациональная.

2x 3

x3 3x

– иррациональная.

x 1

h(x)

sinx

– не является иррациональной, функция

ln x cosx

трансцендентная.

Условимся через R(x1,x2,...,xk ) обозначать рациональную функцию аргументов x1,x2,...,xk .

Примеры:

x 3 x

x3 5 x

sin x 3cos2 x

R sin x,cos x .

1 tgx

Интегралы от иррациональных функций берутся только в отдельных частных случаях. Основной метод – свести какой-нибудь подстановкой интеграл, содержащий иррациональную функцию, к интегралу от рациональной дроби, иначе говоря, рационализировать интеграл.

. R x,pxq ,...,sxr dx

Интеграл

рационализируется

подстановкой

x tk , где

k НОК p,...,s , то есть берём k

так, чтобы все корни извлекались.

Пример.

x t6 t 6

x(1

x) dx 6t

5dt

3(1 t2)

t2 1

6t 6arctgt C 66

6 1

dt 6 dt 6

6arctg6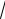x C.

ax b

. R x,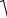 cx d dx.

Интеграл рационализируется подстановкой

ax b

Пример.

cx d

t x 1 t2 t

2 1 t

x 1

2tdt

1 t

x 1

dx 2tdt

t3 t2 t

dt 2 t2 2t 3 dt 2

t3 2t2 6t

t 1

3 6

t 1

6ln

t 1

2(x 1) 6ln1

x 1

Здесь

t3 t2 t |t 1

t3 t2

t2 2t 3

t3 t2 t

2t 3

t 1

2t2

t 1

3t 3

. R x,

dx берём, выделяя полный квадрат под

ax2 bx c

радикалом и

вводя

подстановку,

как

это

делалось

типе

интегрирования простейших дробей, в результате сводим радикал к одному из следующих трёх видов:

1) a2 t2 ; 2) 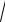a2 t2 ; 3) t2 a2 .

В каждом из этих трёх случаев избавляются от корней ещё одной тригонометрической подстановкой:

1.R t,a2 t2 dt – подстановка t asin .

2.R t,a2 t2 dt – подстановка t atg .

3. R t,

dt – подстановка t

t2 a2

asec .

xdx

cos

Пример. Найти интеграл

2x 3

x2 2x 3

x 1 2 4

t2 4

xdx

x 1 t x t 1

t 1 dt

dx dt

2 2x 3

2 4

sin

2cos

sin

sin2

2cos

sin

lntg 2ctg C ln (x 1) 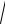x2 2x 3 x2 2x 3 C.

sin 2; tg ? ctg ? t 2

1			t2 4	x2 2x 3
1 ctg2		ctg			;
	sin2		4	2

;

1 cos

t2 4

;

2 t

sin

tg x 1 x2 2x 3 . 2 2

Интегрирование тригонометрических выражений

Интегралы от тригонометрических выражений берутся только в отдельных случаях.

. Основной случай.

R sin x,cosx dx сводится к интегралу от рациональной дроби

универсальной тригонометрической подстановкой tg x t. 2

Пусть tg

t x 2arctgt;

2dt

;

1 t2

2sin

cos

2tg

sin x

;

2 x

1 t2

sin

cos

1 tg

2 x

cos

sin

1 tg

1 t

cos x

2 x

1 t2

sin

cos

1 tg

1 t2

R sin x,cosx dx R

1 t

2 ,

1 t

2 dt R(t)dt.

1 t

Пример.

2dt

t, dx

2dt

1 t2

1 t

1 t 2

1 sin x

sin x

1 t

1 tg

<<< < Предыдущая 1 23 / 113 4 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
07.01.20211.92 Mб11830.pdf
#
07.01.20211.93 Mб21831.pdf
#
07.01.20211.93 Mб221832.pdf
#
07.01.20211.93 Mб51833.pdf
#
07.01.20211.93 Mб951834.pdf
#
07.01.20211.94 Mб21835.pdf
#
07.01.20211.94 Mб21836.pdf
#
07.01.20211.94 Mб41837.pdf
#
07.01.20211.95 Mб251838.pdf
#
07.01.20211.95 Mб01839.pdf
#
07.01.2021333.77 Кб7184.pdf