1749

2

УДК 519.21 ББК 22.171 Ф 33

Рецензенты:

кафедра высшей математики Омского государственного технического университета;

д-р физ. - мат. наук, профессор А.Г. Гринь

Работа одобрена редакционно-издательским советом академии в качестве учебного пособия для студентов инженерно-технических специальностей вузов.

Флаум Р.Г., Завьялов М.А., Чекмарева Т.В. Элементы математической статистики: Учебное пособие. – Омск: Изд-во СибАДИ, 2002. – 56 с.

Данное издание является пособием для студентов технических вузов и может быть использовано аспирантами и инженерами.

Пособие является руководством по математико-статистическим методам обработки опытных данных и их оценки. В нём приведены основные сведения по теории вероятностей с подробным рассмотрением важных для практики законов распределения случайных величин и их характеристики. Изложены методы статистических исследований и оценок, статистическая проверка гипотез, доверительные интервалы, линейная корреляция и регрессия.

Весь материал иллюстрирован примерами. В конце пособия приведены варианты для самостоятельной работы.

Ил. 3. Библиогр.: 5 назв.

3

ВВЕДЕНИЕ

Моделирование реальных явлений с учетом случайных воздействий используется при исследовании любых реальных процессов, на протекание которых влияют случайные факторы.

Моделирование случайных величин – основное содержание метода статистических исследований. Этот метод используют при решении задач, для которых возможно создание вероятностной модели, они опираются на рассмотрение статистических данных о тех или иных совокупностях объектов. При этом под статистическими данными понимаются сведения о числе объектов в обширной совокупности.

Предлагаемое учебное пособие по своему содержанию является руководством для решения конкретных инженерных задач математической статистики. Однако не надо считать, что это пособие может заменить специальные учебники математической статистики, где подробно изложены все положения.

Изложение основ теоретического материала сопровождается примерами выполнения конкретных задач. Это является руководством для самостоятельного решения вариантов, приведённых в конце пособия.

1.ПРЕДМЕТ И ЗАДАЧИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Вобычной речи слова «вероятно», «очень возможно», «правдоподобно» высказываются в понятиях, которые четко не различаются. Однако слово «вероятно» употребляется в определенном смысле, как технический термин теории случайных массовых явлений.

Пример. Мальчики среди новорожденных.

Вродильном доме новорожденные дети регистрируются в том порядке, в каком они рождаются. Мальчики и девочки (М и Д) следуют друг за другом без видимой закономерности, например,

Д М М Д М Д М М Д Д М М М Д Д.

Хотя мы не можем предугадать деталей этой случайной последовательности, вполне можем предсказать важное свойство окончательного результата, получаемого суммированием всех таких регистраций на протяжении достаточно длинного промежутка времени (например, в течение года). Отношение этих двух чисел будет мало отличаться от отношения 51,5:48,5. Если предположить, что число рождений достаточно большое число, то это будет случайное массовое явление значительного объема.

Пусть числа рождений мальчиков, девочек и общего числа рождений соответственно равны 1506959, 1427901, 2934860, назовем отношение

1506959 относительной частотой рождения мальчиков и

2934860

4

1427901 относительной частотой рождения девочек.

2934860

В общем случае, если событие некоторого рода произошло в m слу-

чаях из n, то m мы называем относительной частотой появления этого со- n

бытия.

Приведенный пример показывает, что слово «частота» при строгом изложении является неизбежным термином, а следовательно, дисциплина, предметом изучения которой являются частоты, т.е. теория вероятностей, будет основной. Усвоение вероятностных понятий и овладение методами оперирования с этими понятиями является обязательным для изучения математической статистики.

Цель данной работы – дать базис, на котором строится понимание результатов статистических исследований, с которыми исследователь сталкивается в повседневной работе. Показать, что каждая задача математической статистики является, по существу, задачей теории вероятностей.

Математическая статистика – раздел математики, который посвящен математическим методам систематизации, обработки и использования статистических данных и практическим выводам на основе изучения этих данных.

Поскольку математическая статистика изучает общие закономерности массовых явлений в абстрактной форме, безразличной к природе рассматриваемых объектов, ее выводы могут быть применены к самым разнообразным явлениям при условии, что в них реально осуществляются основные положения общей теоретической схемы.

Задачи теории вероятностей попадают в категорию задач математической статистики, это те задачи, когда данные, на основе которых нужно действовать, оказываются случайными, т.е. имеют вероятностную основу. Напомним кратко некоторые сведения о случайных величинах.

2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ИХ ХАРАКТЕРИСТИКИ

2.1. Дискретные случайные величины

Случайная величина называется дискретной, если она может принимать только конечное или счетное число значений.

Пусть дискретная случайная величина X может принимать n различных значений: x1, x2, x3,…, xn. Для определенности располагаем их в возрастающем порядке.

Пусть для каждого значения xi (i=1, 2, …, n)задана вероятность, с которой случайная величина X принимает именно это значение – p(X=xi)=pi

(i=1, 2, …, n).

5

Функция p(x), связывающая значения случайной величины с соответствующими им вероятностями, представляет собой закон распределения дискретной случайной величины или ряд распределения. Этот закон задается таблицей, где pi =p(X=xi):

Дискретная случайная величина принимает каждое свое значение с ненулевой вероятностью, а значения, которые она принимает с нулевой вероятностью, не учитываются.

Закон распределения полностью описывает дискретную случайную величину.

Рассмотрим основные числовые характеристики дискретной случайной величины математическое ожидание и дисперсию.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятность:

M(X) xk pk .

k 1

В этом случае предполагается, что ряд xk pk сходится абсолютно.

k 1

Математическое ожидание имеет размерность случайной величины. В качестве меры рассеяния случайной величины X около ее математического ожидания берут центральный момент второго порядка – диспер-

сию:

D(X) (xk mx )2 pk

k 1

или D(X) M(X 2 ) M 2 (X).

Дисперсия имеет размерность квадрата случайной величины.

Для характеристики рассеяния случайной величины рассматриваем

среднее квадратическое отклонение (X) 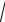D(X) , имеющее ту же

размерность, что и случайная величина X.

Рассмотрим наиболее распространенные законы распределения дискретных случайных величин и их числовые характеристики.

1. Биномиальный закон

Случайная величина X называется распределенной по биномиальному закону с параметрами n и p 0, если X принимает значения 0, 1, 2, …, n

и p(X k) Cnk pk qn k .

Закон распределения имеет вид:

руем это равенство по x, получим n(x y)n kCnk xk 1 yn k . Умножим на x полученное равенство и вернемся к прежним обозначениям, получим:

nx(x y)n kCnk xk yn k или p(p q)n kCnk xk yn k .

Так как p+q = 1, а M(X) kCnk xk yn k , то окончательно M(X) = np.

k 0

Дисперсия D(X) = npq.

2. Закон Пуассона

Случайная величина X называется распределенной по закону Пуассона с параметром a 0, если X может принимать значения 0,1,2,…, k, …,:

P(X k) e a ak . k!

Математическое ожидание и дисперсия случайной величины X в этом случае будут:

D(X) M(X 2 ) M 2 (X) a2 a a2 a.

Таким образом, для распределения Пуассона математическое ожидание и дисперсия равны параметру распределения.

2.2. Непрерывные случайные величины и их характеристики

Случайная величина X называется случайной величиной непрерывного типа, если: а) значения X заполняют промежуток или несколько промежутков на оси Ox; б) существует неотрицательная функция f(x) 0, называемая плотностью распределения вероятностей, что вероятность принадлежности случайной величины X любому промежутку [a, b] равна определенному интегралу от f(x) по этому промежутку:

9

Получили, что D(X) 2 , т.е. дисперсия нормального распределения случайной величины равна квадрату второго параметра.

Среднее квадратическое отклонение случайной величины X будет

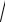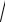D(X) 2 .

При изменении M(X) a график плотности нормально распределенной случайной величины будет смещаться вдоль оси Ox, а вид графика не изменится.

При изменении изменяется вид графика: чем , тем более график имеет форму «всплеска»; при больших значениях кривая имеет пологую форму.

Правило трех сигм. Если в данных исследованиях вероятностями, меньшими чем (1 – 0,9973) 0,003, можно пренебречь, то это означает, что все практически возможные значения нормально распределенной случайной величины X заключены в промежутке (a 3 ; a+3 ).

3. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

Функцией распределения случайной величины X любого типа называется вероятность события X x, где x – любое число. Функция распределения называется иначе интегральным законом распределения и обозначается F(x):

F(x)=P( X x).

С помощью введения функции распределения можно объединить рассмотрение случайной величины дискретного и непрерывного типов с плотностью f(x):

xk pk для дискретногослучая;

xk x

F(x) x

f (t)dt длянепрерывногослучая.

Функция распределения любой случайной величины является неотрицательной, неубывающей функцией аргумента x и изменяется от 0 до 1 при изменении x от ( ) до (+ ).

Вероятность того, что непрерывная случайная величина X примет