5.МАРШРУТИЗАЦИЯ ПЕРЕВОЗОК
5.1.Нахождение кратчайших расстояний (метод потенциалов)
Задача определения кратчайших расстояний является задачей исследования операций. Она относится к классу экстремальных задач.
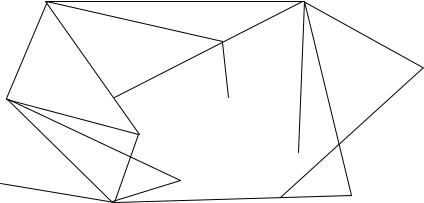
Задана транспортная сеть (рис. 5.1). Пункты транспортной сети
представляют собой вершины, обозначенные А1…А6 |
и Б1…Б8. Заданы |
|||||||
СибАДИ |
||||||||
расстояния между ними, т.е. определены звенья и их длина. |
||||||||
|
Б3 |
|
8,2 |
|
|
Б1 |
|
|
|
|
|
5,8 |
3,0 |
|
|
4,4 |
|
3,7 |
|
3,6 |
3,5 |
|
А5 |
|
|
|
Б2 |
4,5 |
Б7 |
3,6 |
|
А3 |
4,7 |
|
|
|
|
1,4 |
5,0 |
6,1 |
|
|||
5,8 |
|
6,2 |
А1 |
|
|
Б5 |
|
4,6 |
Б6 |
4,7 |
2,3 |
2,2 |
4 |
|
2,3 |
|
|
|
3,9 |
Б4 |
|
5,2 Б8 |
|
А2 |
||
|
|
2,3 |
|
|||||
Рис. 5.1. Схема транспортной сети
Задача решается следующим о разом [6]:
Шаг I. Верш на, от которой требуется определить кратчайшие
расстоян |
я, называется начальной, ей присваивается потенциал vi = 0. |
||
Шаг II. Просматр ваются все звенья, начальные вершины i которых |
|||
имеют потенц алы vi , |
а конечные j – не имеют. |
Определяется значение |
|
потенц алов конечных верш нvi по следующей формуле: |
|||
|
|
vi = vi + cij, |
(5.1) |
где cij –длина звена (i–j), т.е. расстояние между вершинами i и j. |
|||
Из |
всех полученных потенциалов выбирается наименьший |
||
(т.к. определяются |
кратчайшие расстояния) |
его значения |
|
присваивается соответствующей конечной вершине. Звено (i–j) отмечается стрелкой.
Шаг II повторяется до тех пор, пока всем вершинам данной сети не будут присвоены потенциалы.
42
Величина потенциалов у соответствующих вершин показывает кратчайшее расстояние от выбранного начального пункта до данного пункта. Звенья со стрелками образуют кратчайший маршрут движения от начального пункта до остальных.
Принимая за начало сети последовательно каждый ее пункт (вершину) и выполняя расчеты по описанному методу, можно получить таблицу кратчайших расстояний между всеми пунктами сети. [6]
Пример. Предположим, необходимо определить кратчайшие расстояния от вершины А1 до всех остальных вершин сети (см. рис. 4.1).
Шаг I. Принимается vА1 =0.
Шаг II. 1) определяются звенья, для которых вершина А является начальной. На рис. 4.1 – это звенья А1Б7, А1Б2 и А1Б4. Вычисляются потенциалы конечных вершин этих звеньев:
|
vА1Б2 |
= v |
А1 |
+с |
А1Б |
2 |
= 0 +4,5 |
= 4,5; |
||||
|
|
|
А |
|
|
|||||||
|
vА1Б |
4 |
= v |
1 |
+с |
А1Б |
4 |
= 0 +2,3 = 2,3; |
|
|||
|
v |
А1Б |
7 |
= v |
А1 |
+с |
А1Б7 |
= 0 +1,4 |
=1,4 И |
|||
|
|
|
|
|
|
; |
|
|||||
2) выбирается наименьшее значение этих потенциалов: |
||||||||||||
|
min(v |
|
1Б2 |
, v |
1Б4 |
, v |
|
)= v |
=1,4 |
|||
|
|
|
|
|
|
|
1ДБ7 1Б7 ; |
|||||
3) звено А1Б7 |
отмечается стрелкой. Вершине Б1 присваивается |
|||||||||||
потенциала |
|
|
|
|
|
|
|
|
|
|
|
|
значение |
, равное 1,4. |
|
|
|
|
|
|
|
||||
Потенц алы проставляются в квадратах около соответствующих |
||||||||||||
верш н. |
|
|
|
|
|
|
|
|
|
|
|
|
Вновь повторяется шаг II, но за начальную вершину принимается |
||||||||||||
С |
|
ал которой определен. Теперь можно получить |
||||||||||
теперь верш на Б7, |
|
|||||||||||
значен я потенц аловбдля вершин А3, А5, Б5: |
|
|
||||||||||
|
vБ7 А3 |
= vБ7 +сБ7 А3 |
=1,4 +3,6 = 5,0 |
; |
||||||||
|
vБ7 А5 |
|
= vБ7 +сБ7 А5 |
=1,4 +3,5 = 4,9 |
; |
|||||||
|
vБ7Б5 |
= vБ7 +сБ7Б5 |
=1,4 +3,6 = 5,0 . |
|||||||||
43
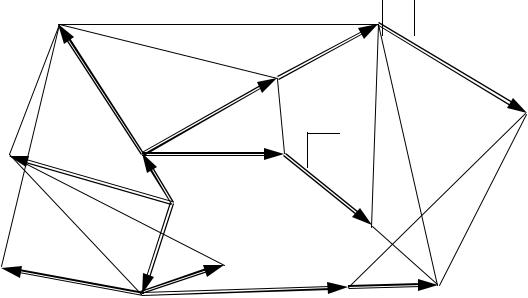
Из всех полученных сейчас и на первом этапе расчета значений потенциалов выбирается наименьшее – vБ7 А5 = 4,9 . Это значение
проставляется в квадрате у вершины А5. Звено Б7А5 отмечается стрелкой. Теперь в качестве начальной вершины используется вершина А5. Продолжая расчеты указанным методом, определяются потенциалы для всех вершин сети. Значения этих потенциалов, проставленные в квадратах, показывают, чему равно кратчайшее расстояние от этих вершин до вершины А1, а звенья, отмеченные стрелками, соответствуют маршруту движения по кратчайшему пути (рис. 5.2).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
Б3 |
|
|
|
|
|
|
8,2 |
|
|
Д |
|
|
|
|
||||||||||||
|
|
|
|
|
5,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б1 7,9 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5,8 |
|
3,0 |
|
|
|
|
|
|
|
|
|
|
4,4 |
|
|
|
|||
3,7 |
|
3,6 |
|
|
|
|
|
|
|
А5 |
4,9 |
|
|
|
|
|
|
|
6,1 |
|
|
|
12,3 |
|
||||||||
|
|
4,5 |
|
|
|
|
|
|
|
3,5 |
|
|
1,7 |
|
|
|
|
|
|
|
|
|
|
|
|
А |
6 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
И |
||||||||||||
|
|
Б2 |
4,5 |
1,4 |
Б7 |
|
|
|
3,6 |
|
3 5,0 |
|
|
|
4,7 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
6,1 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
5,8 |
|
|
1,4 |
|
|
|
|
|
5,0 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
6,2 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
4,6 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
6,2 |
|
|
|
4,7 |
б |
|
|
|
|
|
|
Б5 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
2,3 |
|
|
|
|
|
|
|
|
10, |
|
|
2,3 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Б6 |
|
|
|
|
|
2,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
4 |
4,5 |
|
|
|
|
|
|
|
|
|
|
|
А2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
3,9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9,8 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
и |
2,3 |
|
|
|
5,2 |
|
7,5 |
Б8 |
2,3 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
Б4 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р с. 5.2. Кратчайш е расстояния от вершины А1 до всех вершин сети |
||||||||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Для того, чтобы определить кратчайшие расстояния до всех вершин |
||||||||||||||||||||||||||||||
сети от другой верш ны, |
например Б1, необходимо проделать заново все |
|||||||||||||||||||||||||||||||
расчеты рассмотренным методом, приняв за начало сети выбранную вершину присвоив ей потенциал, равный 0. На основании приведенных расчетов может быть составлена таблица кратчайших расстояний между пунктами транспортной сети (табл. 5.1).
44
Таблица 5.1
Матрица кратчайших расстояний
|
|
А1 |
А2 |
|
А3 |
А4 |
А5 |
А6 |
Б1 |
Б2 |
|
Б3 |
Б4 |
Б5 |
|
Б6 |
Б7 |
Б8 |
|
|
|
А1 |
– |
9,8 |
|
5,0 |
4,5 |
4,9 |
12,3 |
7,9 |
4,5 |
|
5,0 |
2,3 |
10,0 |
|
6,2 |
1,4 |
7,5 |
|
|
|
А2 |
9,8 |
– |
|
7,3 |
9,7 |
9,0 |
4,6 |
6,1 |
12,3 |
|
14,5 |
7,5 |
2,3 |
11,4 |
10,9 |
2,3 |
|
||
|
А3 |
5,0 |
7,3 |
|
– |
9,5 |
1,7 |
9,1 |
4,7 |
9,5 |
|
7,2 |
7,3 |
И |
9,6 |
|
||||
|
|
|
5,0 |
11,2 |
3,6 |
|
||||||||||||||
|
А4 |
4,5 |
9,7 |
|
9,5 |
– |
9,4 |
14,3 |
10,4 |
6,2 |
|
9,5 |
2,2 |
9,8 |
|
6,1 |
5,9 |
7,4 |
|
|
|
А5 |
4,9 |
9,0 |
|
1,7 |
9,4 |
– |
7,4 |
3,0 |
9,5 |
|
5,8 |
7,2 |
6,7 |
11,6 |
3,5 |
11,3 |
|
||
|
А6 |
12,3 |
4,6 |
|
9,1 |
14,3 |
7,4 |
– |
4,4 |
16,0 |
|
12,6 |
11,3 |
6,9 |
15,2 |
10,9 |
6,1 |
|
||
|
Б1 |
7,9 |
6,1 |
|
4,7 |
10,4 |
3,0 |
4,4 |
– |
11,9 |
|
8,2 |
10,2 |
4,7 |
14,0 |
6,5 |
8,4 |
|
||
|
Б2 |
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
||||
|
4,5 |
12,3 |
|
9,5 |
6,2 |
9,5 |
16,0 |
11,9 |
– |
|
3,7 |
4,7 |
14,5 |
|
8,6 |
5,9 |
9,9 |
|
||
|
Б3 |
5,0 |
14,5 |
|
7,2 |
9,5 |
5,8 |
12,6 |
8,2 |
3,7 |
|
– |
7,3 |
12,9 |
|
5,8 |
3,6 |
12,5 |
|
|
|
Б4 |
2,3 |
7,5 |
|
7,3 |
2,2 |
7,2 |
11,3 |
10,2 |
4,7 |
|
7,3 |
– |
9,8 |
|
3,9 |
3,7 |
5,2 |
|
|
|
Б5 |
10,0 |
2,3 |
|
5,0 |
9,8 |
6,7 |
6,9 |
4,7 |
14,5 |
|
12,9 |
9,8 |
– |
13,7 |
8,6 |
4,6 |
|
||
|
Б6 |
6,2 |
11,4 |
11,2 |
6,1 |
11,6 |
А |
5,8 |
3,9 |
13,7 |
|
– |
7,6 |
9,1 |
|
|||||
|
15,2 |
14,0 |
8,6 |
|
|
|
||||||||||||||
|
Б7 |
1,4 |
10,9 |
|
3,6 |
5,9 |
3,5 |
10,9 |
6,5 |
5,9 |
|
3,6 |
3,7 |
8,6 |
|
7,6 |
– |
8,9 |
|
|
|
Б8 |
7,5 |
2,3 |
|
9,6 |
7,4 |
11,3 |
6,1 |
8,4 |
9,9 |
|
12,5 |
5,2 |
4,6 |
|
9,1 |
8,9 |
– |
|
|
|
рассмотрено тремяспособами: |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
5.2. Решение задачи построения маршрутов |
|
|
|
||||||||||||
|
|
|
|
|
|
|
методом совмещенных планов |
|
|
|
|
|
||||||||
|
|
задачи |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Пользуясь материалом лекций, решить задачу 5.2 в соответствии с |
||||||||||||||||||
|
вариантом, заданным преподавателем |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
5.3. Решен е задачи построения развозочных маршрутов |
|||||||||||||||||
С |
|
|
|
маршрутизации |
|
мелкопартионных |
перевозок |
|||||||||||||
|
|
Решен е |
|
|
|
|
||||||||||||||
|
|
- методом |
в ра [3]; |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
- методом сейфов [1]; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
- методом сумм [4, 5]. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Исходная |
информация: взаимное |
расположение |
поставщика и |
|||||||||||||||
потребителей груза представлено на рисунке 54.1. Грузоотправитель находится в пункте А1 , остальные пункты – грузополучатели. Объем
спроса каждого грузополучателя составляет 5 грузовых мест, грузовместимость подвижного состава – 30 грузовых мест. Матрица кратчайших расстояний представлена в табл. 5.1.
45
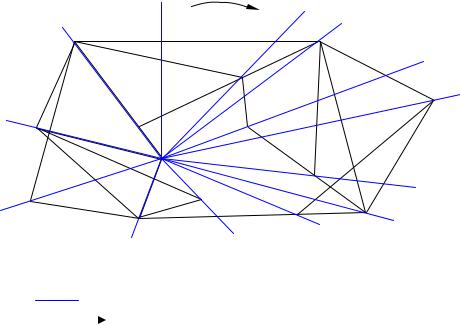
Маршрутизация методом Свира. Объединение грузополучателей в маршруты осуществляется по принципу очерёдности пересечения вершин лучом, исходящим из пункта погрузки, как представлено на рис. 5.3, вследствие чего за методом закрепилось название «Метод истирающего луча».
|
Б3 |
|
|
|
8,2 |
|
|
|
Б1 |
|
|
И |
||||
3,7 |
|
|
3,6 |
|
5,8 |
3,0 |
|
|
|
4,4 |
|
|
||||
|
|
|
3,5 |
|
|
А5 |
6,1 |
|
|
А6 |
|
|||||
|
|
|
|
|
|
|
1,7 |
|
|
|
|
|||||
|
|
|
|
Б7 |
|
3,6 |
|
|
Д |
|
|
|||||
Б2 |
4,5 |
|
|
А3 |
4,7 |
|
|
|
|
|
||||||
|
|
|
1,4 |
|
|
|
5,0 |
6,1 |
|
|
|
|||||
5,8 |
|
|
|
6,2 |
А1 |
|
|
|
|
Б5 |
|
|
4,6 |
|
|
|
Б6 |
4,7 |
|
2,3 |
2,2 |
А4 |
|
|
|
2,3 |
|
|
|
|
|||
|
3,9 |
|
Б4 |
|
|
5,2 Б8 |
2,3 |
|
|
|
|
|
||||
Рис. 5.3. Решение задачи маршрутизации методом Свира («Истирающего луча»): |
||||||||||||||||
|
|
– след пересечения луча с пунктом погрузки; |
|
|
||||||||||||
|
б |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
– направление движения луча |
|
|
|
|
|
|||||||
Например, проводится луч из пункта погрузки сверху вниз, первым |
||||||||||||||||
(при движении по часовой стрелке) |
на пути луча встречается пункт |
А5 , |
||||||||||||||
далее пункт |
Б1 , в соответствии с |
грузоподъёмностью |
автомобиля |
и |
||||||||||||
потребностью |
пунктов в грузе их можно объединить в маршрут |
|
||||||||||||||
А1 – А5 – Б1 – А1 . ПосколькуАгрузовместимость автомобиля использована |
||||||||||||||||
не полностью, |
то дв жен е луча продолжается и в совокупность пунктов |
|||||||||||||||
попадают следующ е вершины. Набор пунктов в маршруты |
|||||||
Суммированиеметодом « |
по столбцам» [4]. |
|
|
|
|||
прекращается, когда полностью использована грузовместимость |
|||||||
транспортного средства. |
|
|
|
|
|
||
Так м |
образом, |
получаем |
наборы пунктов: |
в первый |
маршрут |
||
А1 – А5 – Б1 |
– А3 – А6 – Б5 |
– А2 и во второй маршрут А1 |
– Б8 |
– А4 – Б4 – Б6 – |
|||
Б2 – Б7и. Не включенным в первые два набора пунктов о |
стался лишь |
||||||
пункт Б3 , |
поэтому |
следует |
сформировать маятниковый |
маршрут |
|||
А1Б3 – Б3 А1 .
После определения пунктов, входящих в маршруты, необходимо определить порядок их объезда. С этой целью можно воспользоваться
46
Здесь все пункты маршрута, начиная с А1 , связываются такой замкнутой
линией, которая соответствует кратчайшему пути объезда заданных пунктов. Для реализации метода строится таблица, называемая симметричной матрицей. По главной диагонали в ней расположены пункты, включаемые в маршрут. Цифры показывают расстояние между этими пунктами. Дополнительно в этой матрице имеется итоговая строка – строка сумм. В ней проставляют сумму расстояний по каждому столбцу. Затем строят начальный маршрут из трех пунктов, имеющих максимальную сумму по своему столбцу. В него включают следующий пункт с максимальной суммой. Чтобы определить, между какими пунктами его следует вставить, надо поочередно включать этот пункт между каждой соседней парой. При этом для каждой пары этих пунктов находят величину прироста пробега автомобиля на маршруте при включении в начальный маршрут вновь выбранного пункта.
Величину прироста ∆кр находят по формуле
∆кр = lki +lip −lkp , |
(5.2) |
|
И |
где l – расстояние, км.; k – первый соседний пункт; p – второй соседний пункт; i – включаемый пункт.
Из всех полученных значений ∆ выбирают минимальное, и между
|
|
соответствующими ему пунктами вставляют данный. |
|
|
|||||||
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
Рассмотрим определение очередности пунктов объезда на примере |
|||||||||
|
|
|
|
|
|
А |
|
|
|
||
|
|
первого |
|
б |
|
|
матрицу (табл. 5.2). |
||||
|
|
набора пунктов. Формируем симметричную |
|||||||||
|
|
|
|
|
С мметричная матрица |
|
Таблица 5.2 |
||||
|
|
А1 |
9,8 |
5,0 |
4,9 |
12,3 |
7,9 |
10,0 |
|||
|
|
9,8 |
А2 |
7,3 |
9,0 |
4,6 |
6,1 |
2,3 |
|||
|
|
5,0 |
7,3 |
А3 |
1,7 |
9,1 |
4,7 |
5,0 |
|||
|
|
4,9 |
9,0 |
1,7 |
|
А5 |
7,4 |
3,0 |
6,7 |
||
|
|
12,3 |
4,6 |
9,1 |
7,4 |
А6 |
4,4 |
6,9 |
|||
|
|
7,9 |
6,1 |
4,7 |
3,0 |
4,4 |
Б1 |
4,7 |
|||
|
|
10,0 |
2,3 |
5,0 |
6,7 |
6,9 |
4,7 |
Б |
5 |
||
|
|
|
и |
|
|
|
|
|
|
||
|
|
49,9 |
39,1 |
32,8 |
32,7 |
44,7 |
30,8 |
35,6 |
|||
|
|
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Максимальную сумму имеют столбцы А1 , А6 и А2 , таким образом формируется маршрут из пунктов А1 – А6 – А2 – А1 . Столбец со следующей
по величине суммой соответствует пункту Б5 . Следовательно, необходимо
рассмотреть |
возможность |
включения |
его |
между |
пунктами |
А1 и А6 , А6 и А2 , А2 и А1 . |
|
|
|
|
|
47
∆А1А6 |
= lА1Б5 +lБ5А6 −lА1А6 |
=10 +6,9 −12,3 = 4,6 |
∆А6 А2 |
= lА6Б5 +lБ5А2 −lА6 А2 |
= 6,9 +2,3−4,6 = 4,6 |
∆А2 А1 |
= lА2Б5 +lБ5А1 −lА2 А1 = 2,3+10 −9,8 = 2,5 |
|
Поскольку ∆А2А1 имеет наименьшее значение, то между этими пунктами и следует включать пункт Б5 , таким образом формируется
маршрут А1 |
– А6 |
– А2 – Б5 – А1 . Аналогично рассматриваются все |
||
|
|
И |
|
|
остальные пункты, в результате сформирован маршрут А1 – А5 – |
Б1 – А6 |
– |
||
А2 – Б5 – А3 |
– А1 , |
который иначе можно представить в виде А1 А5 |
– А5Б1 |
– |
Б1 А6 – А6 А2 – А2 Б5 – Б5 А3 – А3 А1 . Также обрабатывается второй набор пунктов, в результате формируется маршрут А1Б7 – Б7 Б2 – Б2 А4 – А4 Б4 – Б4 Б8 – Б8 Б6 – Б6 А1 . Результаты решения задачи маршрутизации методом Свира приведены в табл. 5.3.
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 5.3 |
|
|
Характеристика маршрутов мелкопартионных перевозок, |
|||||||||||
|
|
|
|
|
полученных методом Свира |
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
б |
|
Длина |
Объем |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Маршрут |
|
|
|
|
перевозок, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
маршрута, км |
грузовых мест |
|
А1 А5 – А5Б1 |
– Б1 А6 |
– |
А6 А2 – |
2Б5 |
– Б5 |
3 |
– |
3 |
1 |
26,2 |
30 |
|
|
и |
|
|
|
|
|
|
|
|
||||
|
А1Б7 – Б7 Б2 |
– Б2 А4 |
– |
А4Б4 – Б4Б8 |
|
– Б8 |
Б6 |
– |
Б6 |
1 |
36,2 |
30 |
|
|
|
|
|
|
|
|
А |
|
|
||||
|
А1Б3 – Б3 А1 |
|
|
|
|
|
|
10 |
5 |
||||
|
|
|
|
|
|
|
|
|
|
|
Итого |
72,4 |
65 |
С |
|
|
|
|
|
|
|
|
|
|
|
||
48
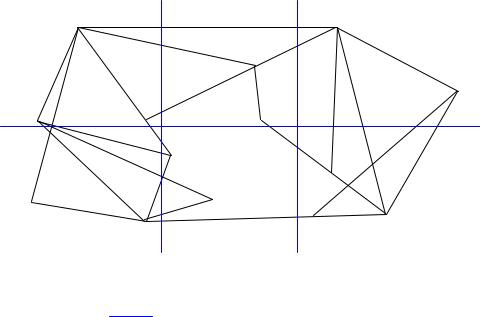
Маршрутизация методом сейфов. Данный метод заключается в том, что на обслуживаемую территорию накладывается сетка и происходит его разбиение на условные районы, как показано на рис. 5.4.
|
|
Б3 |
|
|
|
8,2 |
|
|
Б1 |
|
|
|
|
|
|
|
5,8 |
3,0 |
|
|
И |
||
|
3,7 |
|
3,6 |
|
|
|
|
А5 |
|
|
4,4 |
|
|
|
3,5 |
|
|
|
|
|
|||
|
|
|
Б7 |
|
3,6 |
1,7 |
|
6,1 |
А6 |
||
|
Б2 |
4,5 |
|
|
А3 |
4,7 |
|
|
|||
|
|
|
|
1,4 |
|
5,0 |
6,1 |
||||
|
5,8 |
|
6,2 |
А1 |
|
|
|
Б5 |
|
4,6 |
|
|
4,7 |
|
А4 |
|
|
|
|||||
|
Б6 |
2,3 |
2,2 |
|
|
2,3 |
|
||||
|
|
|
|
А2 |
|||||||
|
3,9 |
|
|
|
|
|
|
|
|||
|
|
Б4 |
|
|
5,2 Б8 |
2,3 |
|||||
|
|
|
|
|
|||||||
|
|
|
|
|
А |
|
|
||||
|
Рис. 5.4 Решение задачи маршрутизации методом сейфов: |
||||||||||
|
|
|
|
|
– граница условного района |
|
|||||
В данном случае территория разбивается на 6 условных районов, |
|||||||||||
каждый |
|
обслуживает |
отдельный |
автомобиль. Наиболее |
|||||||
из которых |
|
|
|
|
|||||||
широкое применение данный метод находитДпри составлении маршрутов |
|||||||||||
помашинных перевозок, но данном случае используется в развозочной |
|||||||||||
автотранспортной системе перевозки грузов. |
|
|
|
||||||||
Например |
|
|
|
|
|
|
|
||||
|
|
, как показано на рис. 5.4, во втором районе находятся |
|||||||||
верш ны А5 |
А3. В данный район автомобилю планируется выполнить |
||||||||||
маршрут |
А1 А5 – А5 А3 – А3 А1 , |
что ы полностью удовлетворить потребность |
|||||||||
|
данного района в грузе, равную 10 т. Так составляются маршруты для |
||||||||||
С |
|
|
|
|
|
|
|
|
|
||
|
каждого район , результаты занесены в табл. 5.4. |
|
|
|
|||||||
|
|
|
План маршрутов мелкопартионных перевозок, |
Таблица 5.4 |
|||||||
|
|
|
|
полученных методом Сейфов |
|
|
|
||||
|
№ |
Маршрут |
Груз, грузовые места |
|
Расстояние, км |
|
|||||
|
Завоз |
Завоз |
Завоз |
|
|
|
|
||||
|
п/п |
Lг1 |
Lг2 |
Lг3 |
Lх |
||||||
|
|
|
в п. 1 |
в п. 2 |
в п. 3 |
||||||
|
|
|
|
|
|
|
|
||||
|
1 |
2 |
|
3 |
4 |
5 |
|
6 |
7 |
8 |
9 |
|
|
|
|
Первый условный район |
|
|
|
||||
|
1 |
А1 - Б2 - Б3 - Б7 - А1 |
5 |
5 |
5 |
|
4,5 |
3,7 |
3,6 |
1,4 |
|
|
|
|
|
Второй условный район |
|
|
|
||||
|
2 |
А1 - А5 - А3 - А1 |
5 |
5 |
- |
|
4,9 |
1,7 |
- |
5,0 |
|
49
Окончание табл.5.4
Третий условный район
3 |
А1 - Б1 - А6 - А1 |
5 |
|
5 |
- |
7,9 |
4,4 |
- |
12,3 |
||
|
|
|
|
Четвертый условный район |
|
|
|
||||
4 |
А1 - Б4 - Б6 - А1 |
5 |
|
5 |
- |
2,3 |
3,9 |
- |
6,2 |
||
|
|
|
|
|
Пятый условный район |
|
|
|
|||
5 |
А1 |
- А4 |
- А1 |
5 |
|
- |
- |
4,5 |
- |
- |
4,5 |
|
|
|
|
|
Шестой условный район |
|
|
|
|||
6 |
А1 - Б5 |
- А2 |
- Б8 - А1 |
5 |
|
5 |
5 |
10 |
2,3 |
2,3 |
7,5 |
Порядок объезда пунктов маршрута может быть определен также методом суммирования по столбцам. Основные параметры развозочных маршрутов, полученных методом сейфов, представлены в табл. 4.5.
|
|
|
|
|
|
|
|
Таблица 5.5 |
Характеристика маршрутов мелкопартионных перевозок, |
||||||||
|
полученных методом сейфов |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
Объем |
|
|
Маршрут |
|
|
|
лина маршрута, |
И |
||
|
|
|
|
|
|
км |
|
грузовых мест |
А1 |
- Б2 - Б3 - Б7 |
- |
1 |
|
|
13,2 |
|
15 |
|
б |
|
|
|
|
|||
|
А1 - А5 - А3 - |
1 |
|
|
|
11,6 |
|
10 |
|
|
|
|
Д |
|
|
||
|
А1 - Б1 - А6 - 1 |
|
|
24,6 |
|
10 |
||
|
А1 - Б4 - Б6 - 1 |
|
|
|
12,4 |
|
10 |
|
|
А1 - А4 - 1 |
|
|
|
|
9,0 |
|
5 |
А1 - Б5 - А2 - Б8 - А1 |
|
|
22,1 |
|
15 |
|||
|
|
|
|
Итого |
|
92,9 |
|
65 |
Маршрут зац я методом сумм. Решение находится путем последовательного расчета в следующей последовательности.
СБ4 – А1 – Б7 , и из них выбирают наименьшее. При этом нельзя выбирать
Шаг 1. Нахожден е кратчайшей связывающей сети.
Она определяется следующим образом. На сети находят наименьшее
звено. В рассматр ваемом случае звено А1 – Б7 = 1,4 км. Затем
рассматривают все звенья, связанные одной из своих вершин с |
||
выбраннымизвеном (звенья А1 – А2 , …, А1 – А8 , …, Б7 – А2 ,…, Б7 – Б8 ). Из них |
||
выбирают звено |
с наименьшим расстоянием А1 – Б4 |
= 2,3 км. Далее |
рассматриваются |
звенья, связанные с вершинами |
полученной линии |
звено, соединяющее две ранее включенные в сеть вершины, например звено Б7 – Б4 , даже если оно наименьшее из всех, связанных с выбранной
сетью. Если звенья, связанные с уже выбранной сетью, имеют одинаковое наименьшее расстояние, то из них можно выбрать любое. Далее опять
50
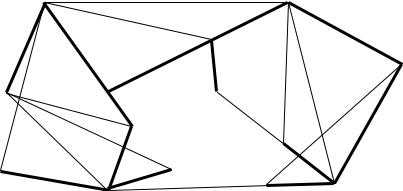
рассматривают все звенья, связанные с вершинами полученной ломаной линии и из них выбирают наименьшее, и так до тех пор, пока не будут выбраны сети. Затем составляют схему кратчайшей связывающей сети.
Составленная транспортная сеть представлена на рис. 5.5. Количество доставляемого в каждый пункт груза будет одинаковым –
15 единиц груза, также как и вывозимого – 15 единиц груза. |
|
||||||||||||||
|
Б |
|
|
|
8,2 |
|
|
|
Б1 |
|
|
|
И |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
5,8 |
3,0 |
|
|
|
|
|
4,4 |
|
|||
3,7 |
|
3,6 |
|
|
|
|
А5 |
|
|
|
|
|
|
||
|
|
3,5 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1,7 |
|
|
|
|
6,1 |
|
|
А6 |
||
Б2 |
|
Б7 |
|
|
3,6 |
|
А3 |
Д |
|
||||||
|
4,5 |
|
|
1,4 |
|
|
|
5,0 |
4,7 |
6,1 |
|
|
|||
5,8 |
|
6,2 |
А1 |
|
|
|
|
Б5 |
|
|
|
4,6 |
|
||
Б6 |
4,7 |
2,3 |
2,2 |
А4 |
|
|
|
|
|
2,3 |
|
|
|
||
|
3,9 |
Б4 |
А |
|
|
|
А2 |
|
|||||||
|
|
|
5,2 Б8 |
|
2,3 |
|
|
|
|||||||
|
Рис. 5.5 Кратчайшая связывающая сеть: |
|
|||||||||||||
|
|
– |
кратчайшей связывающей сети |
|
|||||||||||
Шаг 2. На ор пунктов в маршруты. По каждой ветви сети, начиная с той, которая имеет наи ольше число звеньев, группируют пункты в маршруты с учетом количества ввозимого и вывозимого груза и вместимости подвижного состава. Если все пункты данной ветви не могут
быть включены в маршрут, то |
лижайшие к другой ветви пун |
кты |
групп руются вместе с пунктами этой ветви. |
|
|
При этом в соответств |
с условием рассматриваемого примера по |
|
каждому маршруту про звод тся доставка не более 30 грузовых мест. |
||
Шаг 3. Определенребрае очередности объезда пунктов |
маршрута. |
|
Решается методом сумм рования по столбцам. Результаты решения задачи представлены в табл. 5.6.
|
Группировка пунктов объезда по маршрутам |
Таблица 5.6 |
|||||
|
|
||||||
|
|
|
|
|
|
Длина маршрута, |
Объем |
|
|
Маршрут |
|
перевозок, |
|||
|
|
|
км |
||||
|
|
|
|
|
|
грузовых мест |
|
|
|
|
|
|
|
|
|
|
А1 - Б2 - Б3 - А3 - Б7 - А1 |
19,0 |
20 |
||||
|
С |
|
|
|
|
|
|
А |
- Б |
- А |
- Б |
- А |
16,8 |
15 |
|
|
1 |
4 |
4 |
6 |
1 |
||
|
А1 - А5 - Б1 - А6 - Б5 - А2 - Б8 - А1 |
31,3 |
30 |
||||
|
|
|
|
|
Итого |
67,1 |
65 |
51