
- •ВВЕДЕНИЕ
- •1. ПОСТАНОВКА ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
- •1.1. Пояснительный материал
- •1.2. Задачи
- •Контрольные вопросы и задания
- •3.1. Пояснительный материал
- •3.3. Задачи
- •Контрольные вопросы
- •4.2. Методы составления первого допустимого плана перевозок (метод двойного предпочтения, метод аппроксимации Фогеля и статистический метод)
- •4.4. Решение транспортной задачи с помощью MS Excel
- •4.5. Задачи
- •Контрольные вопросы и задания
- •5. МАРШРУТИЗАЦИЯ ПЕРЕВОЗОК
- •5.1. Нахождение кратчайших расстояний (метод потенциалов)
- •5.4. Задачи
- •Контрольные вопросы и задания
- •Библиографический список
4.2. Методы составления первого допустимого плана перевозок (метод двойного предпочтения, метод аппроксимации Фогеля и статистический метод)
Метод двойного предпочтения. Он заключается в нахождении минимального элемента в столбце и его проверке на минимальность в строке. Если этот элемент окажется наименьшим и по столбцу, и по строке, то в данную клетку записывают максимально возможную, и все элементы данной строки или столбца из дальнейшего рассмотрения исключают.
Если минимальный элемент в столбце не является минимальным в строке, то временно этот столбец из рассмотрения опускают и переходят к следующему. После рассмотрения всех столбцов возвращаются к пропущенным и операцию повторяют. Так поступают до тех пор, пока не
поскольку спрос грузополучателя Б1 Дудовлетворен полностью, то соответствующая строка вычеркивается. Столбец А5 остается для
будет получено базисное распределение [6]. |
|
Пример. Клетками с наименьшим расстоянием и в строке и в |
|
столбце являются клетки Б1А5, Б4А4, Б5А2, Б7А1 и Б8А2. Поэтому в |
|
|
И |
первую очередь заполняются эти клетки, а соответствующие столбцы |
|
внос тся загрузка 145 т, в клеткуАБ7 1 вносится загрузка 140 т и в клетку Б8А2 45 т; з дальнейшего рассмотрения исключаются строка Б5, столбец А1 столбец А2 вследств е удовлетворения потребности в перевозках.
(строки) по мере удовлетворения из дальнейшего рассмотрения
исключаются. Так, первая поставка 140 т заносится в клетку Б1А5,
Все оп санные бдейств я повторяются с оставшимися строками и столбцами до тех пор, пока потребности всех грузоотправителей и грузополучателей в перевозках не будут полностью удовлетворены,
дальнейшего решения задачи, т.к. у данного грузоотправителя еще остались не вывезенными 10 т. В ячейку Б4 4 вносятся 165 т, вследствие чего столбец Б4 из рассмотрения исключатся, аналогично в клетку Б5А2
результат решен |
я задачи представлен в табл. 4.5. |
При |
данного метода была получена схема первого |
допустимогопримененииплана распределения, суммарная транспортная работа равна |
|
С |
|
Р4 = 6602,5 т·км. |
|
26

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.5 |
|
Опорный план, построенный методом двойного предпочтения |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ГП |
|
|
|
|
|
|
ГО |
|
|
|
|
|
|
Объем |
||
А1 |
|
А2 |
А3 |
|
А4 |
А5 |
А6 |
спроса, т |
|
|||||||
|
|
|
|
|||||||||||||
Б1 |
|
7,9 |
|
6,1 |
|
4,7 |
|
|
10,4 |
|
3,0 |
|
4,4 |
140 |
|
|
|
|
|
|
|
|
|
|
|
|
140 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
И |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б2 |
|
4,5 |
|
12,3 |
|
9,5 |
|
|
6,2 |
|
3,5 |
|
16,0 |
190 |
|
|
|
|
|
|
|
155 |
|
|
|
10 |
25 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Б3 |
|
5,0 |
|
14,5 |
|
7,2 |
|
|
9,5 |
|
5,8 |
|
12,6 |
120 |
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2,3 |
|
7,5 |
|
7,3 |
|
|
2,2 |
|
7,2 |
|
11,3 |
|
|
|
Б4 |
|
|
|
|
|
55 |
|
165 |
Д |
220 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Б5 |
|
10,0 |
|
2,3 |
|
5,0 |
|
|
9,8 |
|
6,7 |
|
6,9 |
145 |
|
|
|
|
|
145 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б6 |
|
6,2 |
|
11,4 |
|
11,2 |
|
|
6,1 |
|
11,6 |
|
15,2 |
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б7 |
|
1,4 |
|
10,9 |
|
3,6 |
|
|
5,9 |
|
3,5 |
|
10,9 |
150 |
|
|
140 |
|
|
|
10 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Б8 |
|
7,5 |
|
2,3 |
|
9,6 |
|
|
7,4 |
|
11,3 |
|
6,1 |
120 |
|
|
|
|
|
45 |
|
|
|
|
|
|
|
75 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|||
Наличие |
140 |
|
190 |
340 |
|
165 |
150 |
200 |
1185 |
|
||||||
груза, т |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Метод аппроксимации Фогеля. При этом способе первое допустимое
стоит ливыбираютона столбце или в строке разностей. В клетку с минимальным |
|
распределение является |
лизким к оптимальному и, по сути, является |
приближенным решением задачи. |
|
При этом спосо е |
сходнаяАматрица дополняется столбцом и строкой |
разностей. Затем в каждой строке и каждом столбце матрицы отыскивают |
|
два на меньш х элемента определяют абсолютную разность между ними, которую заносят соответственно разности по строке в столбец разностей, разности по столбцам – строку разностей. Если две клетки в одной и той же строке ли столбце меют одинаковые значения элементов, то разность
Сэлементом данной строки или столбца заносят максимально возможную загрузку, учитывая ресурс поставщика и спрос потребителя. Наибольшая разность зачеркивается. Если спрос потребителя полностью удовлетворен или ресурс поставщика исчерпан, в соответствующей строке или столбце разностей проставляется буква «К» (Конец) и данная строка или столбец из дальнейшего рассмотрения выбывает [6] (табл. 4.6).
для этой строки |
ли столбца принимается равной нулю. |
Затем |
наибольшую величину разности независимо от того, |
27

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.6 |
|
|
|
|
|
Опорный план, построенный методом аппроксимации Фогеля |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ГП |
|
|
|
|
|
|
|
|
|
|
ГО |
|
|
|
|
|
|
|
|
|
Объем |
Столбец |
||
|
|
|
А1 |
А2 |
|
А3 |
|
|
А4 |
|
|
А5 |
А6 |
|
спроса, |
разности |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
Б1 |
|
|
|
|
7,9 |
|
6,1 |
|
|
|
4,7 |
|
|
10,4 |
|
|
3,0 |
|
4,4 |
140 |
1,4; 1,4; 1,4; 1,4; |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,3; 0,3; 0,3; 0,3; |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
140 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,3; 0,3; 0,3 К |
|
||
|
Б2 |
|
|
|
|
4,5 |
|
12,3 |
|
|
|
9,5 |
|
|
|
6,2 |
|
|
3,5 |
|
16,0 |
190 |
1,0; 1,0; 1,0; 6,0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,8; 2,8; 2,8; 2,8; |
|
||
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
150 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6,5 К |
|
||||
|
|
|
|
|
|
5,0 |
|
14,5 |
|
|
|
7,2 |
|
|
|
9,5 |
|
|
5,8 |
|
12,6 |
|
0,8; 0,8; 0,8; 1,4; |
|
|
|
Б3 |
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
Д |
120 |
5,4; 5,4; К |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Б4 |
|
|
|
|
2,3 |
|
7,5 |
|
|
|
7,3 |
|
|
|
2,2 |
|
|
7,2 |
|
11,3 |
220 |
0,1; 4,9; 4,9; 0,1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,2; 0,2; 0,2; 0,2; |
|
||
|
|
|
40 |
|
|
|
15 |
|
|
165 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4,0; 4,0 К |
|
||||||||
|
Б5 |
|
|
|
|
10,0 |
|
2,3 |
|
|
|
5,0 |
|
|
|
9,8 |
|
|
6,7 |
|
6,9 |
145 |
2,7; 2,7; 2,7; 2,7; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,7; 2,7; 2,7; 2,7; |
|
||
|
|
|
|
|
|
70 |
|
15 |
|
|
|
|
|
|
|
|
60 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,9; 1,9; 1,9 К |
|
||||||
|
|
|
|
|
|
6,2 |
|
11,4 |
|
|
11,2 |
А |
11,6 |
|
15,2 |
|
|
|
|||||||
|
Б6 |
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
||||
|
Б7 |
|
|
|
|
1,4 |
|
10,9 |
|
|
|
3,6 |
|
|
|
5,9 |
|
|
3,5 |
|
10,9 |
150 |
2,1; 2,1; 2,1; 0,1; |
|
|
|
|
|
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Б8 |
|
|
|
|
7,5 |
|
2,3 |
|
|
|
9,6 |
|
|
|
7,4 |
|
|
11,3 |
|
6,1 |
120 |
3,8; 3,8; 3,8; 3,8; |
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наличие |
140 |
190 |
|
340 |
|
165 |
|
150 |
200 |
|
1185 |
|
|
|||||||||||
|
груза, т |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Строка |
|
0,9; 0,9; 0,9; |
0,0; 0,0; 0,0; |
1,1; 1,1; 1,1; |
|
3,9;К 0,5; 0,5; 0,5; |
1,7;1,7; 1,7; |
|
|
|
||||||||||||||
|
|
|
поставки |
|
|
|
|
|
|
|
|
0,5; К 1,7; 1,7; 1,7; |
|
|
|
||||||||||
|
разности |
К |
0,0; 0,0; 0,0; |
1,1; 1,1; 0,3; |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
0,0; 3,8; К |
0,3; 0,3; 0,3; |
|
|
|
|
|
|
|
1,7; 2,5; 2,5; |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
0,3; 0,3 К |
|
|
|
|
|
|
|
2,5; 2,5 К |
|
|
|
|||||
|
После заполнен я клетки разности пересчитывают, и операции вновь |
||||||||||||||||||||||||
до тех пор, пока не |
удет составлена |
программа |
распределения. При |
||||||||||||||||||||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
нал ч |
|
|
двух од наковых на больших разностей загрузку записывают в |
||||||||||||||||||||||
клетку, |
которая |
меет на меньший элемент по строке или столбцу. Такая |
|||||||||||||||||||||||
клетка называется едловой. Последние распределения можно сделать без выч слен я разностей, поскольку остается несколько незагруженных клеток, которые очевидны [6].
Пример. После подсчета разностей наибольшая оказалась в строке А6 и равна 33, а наименьшее расстояние – в клетке А6Б8, куда и заносится максимальная загрузка Q=120 т. Потребность удовлетворена, ставим букву «К». Считаем разности заново, максимальная оказалась в строке А1 и равна 12. В клетку А1Б2 с минимальным расстоянием 9 вносим максимальную загрузку Q=140 т, результат решения задачи представлен в табл. 3.6.
28
При применении данного метода была получена схема первого допустимого плана распределения, суммарная транспортная работа равна
Р5 = 5035,5 т·км.
Статистический метод. Метод состоит в определении «наиболее выгодных» клеток и их заполнении в определенной очередности, а эффективность статистического метода состоит в том, что клетки матрицы для заполнения определяют все сразу, а не последовательно как обычно, что значительно упрощает решение.
Показатели очередности заполнения клеток исходной матрицы
обеспечивает максимальное приближение к минимально необходимым
рассчитываются так: |
|
|
dij = cij – (Ci + Cj), |
|
(4.1) |
где cij – расстояние перевозки; Сi – среднее |
расстояние по i |
строке; |
Cj – среднее расстояние по j столбцу. |
|
(т.е. по |
Заполнение матрицы начинают с клетки с наибольшим |
||
|
И |
|
модулю) по величине показателем очередности, поскольку это |
||
А |
|
|
затратам. При этом в клетку заносят максимально возможную поставку с |
|
|
б |
учетом всех факторов. Заполнение клеток продолжается до полного |
|
удовлетворения спроса на транспортныеДуслуги за счет наличных |
|
ресурсов [6]. |
|
Пример. Сначала нео ходимо найти средние значения расстояний |
|
проставляютсязагрузки исходя из возможностей поставщиков и потребителей.
для каждой строки и каждого стол ца, например для строки А1=6,08 км, а
для столбца Б1=5,6 км занести их в дополнительные строку и столбец
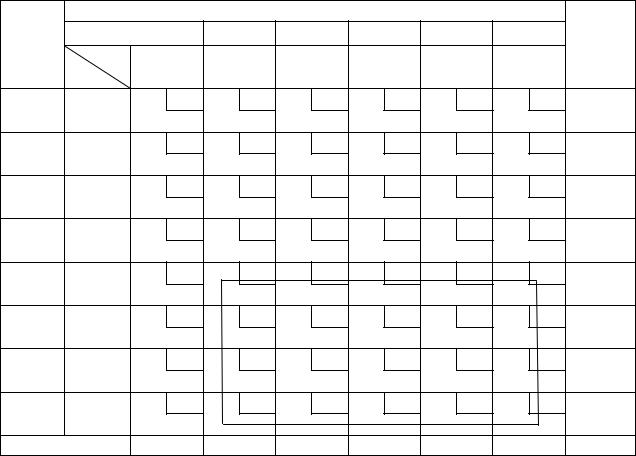
соответственно (та л. 4.7). Затем определяется очередность заполнения клеток матр цы. На меньшее значение имеет клетка Б8А2, именно эта клетка будет заполняться первой при распределении загрузки. В табл. 4.7 порядковые номера заполнен я клеток находятся в правом верхнем углу каждой клетки.
СЕсли спрос полностью удовлетворен или груз полностью вывезен, соответствующие строки и столбцы из рассмотрения исключаются.
ледующ м шагом является построение опорного плана. Для этого в клетки в соответствии с присвоенным им порядком очередности
29

|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.7 |
||
|
|
|
Показатели очередности заполнения клеток |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ГП |
|
|
|
|
|
ГО |
|
|
|
|
Средние |
|||
|
А1 |
А2 |
А3 |
А4 |
А5 |
А6 |
|
|
|||||||
|
|
|
|
||||||||||||
|
Б1 |
|
42 |
|
22 |
|
21 |
|
46 |
|
15 |
|
3 |
6,08 |
|
|
-3,78 |
-22,23 |
-8,65 |
-2,87 |
-9,65 |
-12,11 |
|
||||||||
|
|
|
|
||||||||||||
|
Б2 |
|
11 |
|
40 |
|
30 |
|
16 |
|
4 |
|
44 |
27,12 |
|
|
СибАДИ |
|
|||||||||||||
|
|
-28,22 |
73,63 |
-24,87 |
-28,10 |
-30,19 |
-21,54 |
|
|
||||||
|
Б3 |
|
12 |
|
45 |
|
18 |
|
28 |
|
10 |
|
27 |
9,10 |
|
|
-9,70 |
-16,85 |
-9,16 |
-6,79 |
-9,88 |
-6,93 |
|
||||||||
|
|
|
|
||||||||||||
|
Б4 |
|
17 |
|
25 |
|
32 |
|
7 |
|
33 |
|
37 |
6,30 |
|
|
-9,60 |
-21,05 |
-6,26 |
-11,29 |
-5,68 |
-5,43 |
|
||||||||
|
|
|
|
||||||||||||
|
Б5 |
|
48 |
|
2 |
|
20 |
|
41 |
|
29 |
|
8 |
6,78 |
|
|
-2,38 |
-26,73 |
-9,04 |
-4,17 |
-6,67 |
-10,31 |
|
|
|||||||
|
|
|
|
||||||||||||
|
Б6 |
|
14 |
|
24 |
|
31 |
|
6 |
|
38 |
|
35 |
10,28 |
|
|
-9,68 |
-21,13 |
-6,35 |
-11,37 |
-5,26 |
-5,51 |
|
|
|||||||
|
|
|
|
||||||||||||
|
Б7 |
|
9 |
|
43 |
|
13 |
|
23 |
|
19 |
|
34 |
6,03 |
|
|
-10,23 |
-13,38 |
-9,70 |
-7,32 |
-9,11 |
-5,56 |
|
|
|||||||
|
|
|
|
||||||||||||
|
Б8 |
|
36 |
|
1 |
|
39 |
|
26 |
|
47 |
|
5 |
7,36 |
|
|
-5,47 |
-27,92 |
-5,03 |
-7,15 |
-2,64 |
-11,70 |
|
|
|||||||
|
|
|
|
||||||||||||
|
Средние |
5,60 |
22,25 |
7,26 |
7,19 |
6,58 |
10,43 |
– |
|
||||||
Если клетка со следующим порядковым номером находится в строке или столбце уже исключенных, груз распределяется в клетку с номером, следующим за этой клеткой. Так, в клетку Б8 1 с порядковым номером 1 распределяется 120 т груза, при этом строка Б8 из р ассмотрения исключается. Следующее распределение груза производится в клетку Б5 2, с порядковым номером 2, действия выполняются до тех пор, пока
весь груз не |
удет распределен полностью. Опорный план, полученный |
|
стат ст ческ |
м методом, пр веден в табл. 4.8. |
|
При пр менен |
данного метода была получена схема первого |
|
допуст мого плана распределения, суммарная транспортная работа равна
Р6=5427,5 т·км.
30
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.8 |
||
|
Опорный план, построенный статистическим методом |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ГП |
|
|
|
|
|
|
ГО |
|
|
|
|
|
|
|
|
Объем |
||
А1 |
А2 |
|
А3 |
|
А4 |
|
А5 |
А6 |
|
спроса, т |
|
|||||||
|
|
|
|
|
|
|||||||||||||
Б1 |
|
7,9 |
|
6,1 |
|
|
4,7 |
|
|
10,4 |
|
|
3,0 |
|
4,4 |
|
140 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
140 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б2 |
|
4,5 |
|
12,3 |
|
|
9,5 |
|
|
6,2 |
|
|
3,5 |
|
16,0 |
|
190 |
|
|
|
|
|
|
40 |
|
|
|
|
150 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Б3 |
|
5,0 |
|
14,5 |
|
|
7,2 |
|
|
9,5 |
|
|
5,8 |
|
12,6 |
|
120 |
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б4 |
|
2,3 |
|
7,5 |
|
|
7,3 |
|
|
2,2 |
|
|
7,2 |
|
11,3 |
|
220 |
|
|
|
|
|
|
155 |
|
65 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Б5 |
|
10,0 |
|
2,3 |
|
|
5,0 |
|
|
9,8 |
|
|
6,7 |
|
6,9 |
|
145 |
|
|
|
70 |
|
15 |
|
|
|
|
|
|
60 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Б6 |
|
6,2 |
|
11,4 |
|
|
11,2 |
|
|
6,1 |
|
|
11,6 |
|
15,2 |
|
100 |
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б7 |
|
1,4 |
|
10,9 |
|
|
3,6 |
|
|
5,9 |
|
|
3,5 |
|
10,9 |
|
150 |
|
140 |
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Б8 |
|
7,5 |
|
2,3 |
|
|
9,6 |
|
|
7,4 |
|
|
11,3 |
|
6,1 |
|
120 |
|
|
|
120 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Наличие |
140 |
190 |
|
340 |
|
165 |
|
150 |
200 |
|
1185 |
|
||||||
груза, т |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3. Оптимизация первоначального распределения |
||||||||||||||||
|
|
|
|
|
|
|
методом МОДИ |
|
|
|
|
|
||||||
Последовательность |
вычислений |
методом |
(модифицированного |
|||||||||||||||
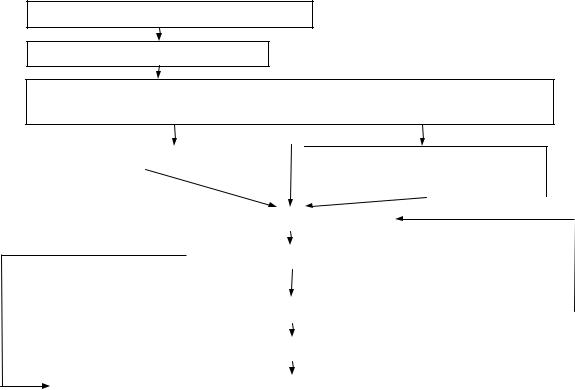
СибАДИопределен я дополн тельных индексов) МОДИ может быть представлена в в де блок-схемы (р с. 4.1) [10].
Для оценки опт мальности решения подбираются потенциалы следующ м образом. После получения опорного плана производится промежуточная проверка: необходимо, чтобы количество груза, записанное по клеткам каждого столбца матрицы, равнялось объему наличия в данном столбце (пункте), а количество груза, записанное по клеткам строки матрицы, равнялось объему потребления в этой строке.
Потенциал для первой строки таблицы берется равным нулю. Затем по расстояниям загруженных клеток подбираются потенциалы для других строчек столбцов таблицы так, чтобы расстояние каждой загруженной клетки равнялось сумме потенциалов строки и столбцов, в которых находится данная клетка.
31
Формирование матрицы решения
Построение опорного плана
Сравнение числа занятых клеток матрицы N
с числом (m + n −1)= K
|
N < K |
|
N = K |
|
|
|
|
|
N > K |
||||
|
|
|
|
|
|
|
|
|
|
|
И |
||
Загрузка недостающих клеток |
|
|
Освобождение от лишних |
||||||||||
|
|
|
|
|
|
|
загруженных клеток |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Потенциальной |
|
Определение индексов |
|
|
|
|
|
||||||
|
клетки нет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проверка на оптимальность |
|
|
|
||||||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Потенциальная клетка есть |
|||||
|
|
Построение контура |
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
Перераспределение загрузки |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|||||||
|
Конец вычислений. Получен оптимальный вариант |
|
|
||||||||||
Рис. 4.1. Блок-схема последовательности вычислений методом МО И |
|||||||||||||
|
б |
|
|
|
|
|
|
|
|
||||
Проверка оптимальности полученногоДопорного плана:
1. Для проверки оптимальности опорного плана определяют специальные индексы, проставляемые в клетках вспомогательной строки
и столбца [3, 4, 5, 6, 10]. В клетке вспомогательного столбца, |
||
число |
|
|
соответствующей первой строке Б1, записываем ноль. Остальные индексы |
||
рассч тывают, спользуя загруженные клетки, по формуле |
|
|
|
αi +βj = lk , |
(4.2) |
Сгде m − число столбцов в матрице; n − число строк в матрице.
где αi − ндекс в клетке вспомогательной строки; βj − индекс в клетке вспомогательного столбца; lk − расстояние в загруженной клетке.
Для нахожден я всех числовых значений индексов необходимо,
чтобы |
загруженных клеток К в матрице равнялось числу |
|
|
K = m + n −1, |
(4.3) |
Если количество загруженных клеток в матрице будет меньше числа К, то необходимо искусственно догрузить недостающее количестве клеток, для этого в них записывают ноль. Ноль следует ставить в такую незагруженную клетку матрицы, в которой имеется минимальный элемент Cij и один индекс для нее известен.
32
В соответствии с изложенным правилом в клетке вспомогательного столбца β1 записываем ноль.
2. Определение потенциальной клетки. После определения индексов находим такие незагруженные клетки в матрице, для которых бы выполнялось следующее правило:
αi +βj > lg , |
И |
(4.4) |
где lg − расстояние в незагруженной клетке, км.
Если не все клетки имеют сумму потенциалов меньше, чем указанное в них расстояние, то для клеткиДс наибольшей разницей
строится контур, по которому осуществляется перераспределение. Контур
строится таким образом, чтобы один из углов контура лежал в наиболее
потенциальной клетке, а остальные углы – в загруженных клетках. Затем
все клетки, вошедшие в контур, отмечаются знаками «+» и «−», начиная с
угла, лежащего в потенциальной клетке, которому присваивается знак
«+». Затем выявляют наименее загруженную клетку, занятую
отрицательным углом контура. Количество груза, указанное в этой клетке
отнимется из всех отрицательных углов и прибавляется к значениям, находящимся во всех положительных углах контура. После перераспределения потенциалы считают заново и находят суммы для каждой клетки. Если новое распределение опять не является оптимальным, то операцию повторяют, пока распределение не станет оптимальным [3, 4, 5, 6, 10].
Ниже рассмотрен пример оптимизации опорного плана, полученного |
|
методом аппрокс мац |
ФогеляА(та л. 4.6). |
Вспомогательный |
ндекс β1 принимается равным 0, значения |
остальных вспомогательных индексов рассчитаны по формуле (4.2),
получены следующ е значен я потенциалов: |
|
|||
|
|
б |
|
|
β1=0; |
|
|
β7=l7,3-α3=1,1; |
β4=l4,3-α3=4,8; |
α6=l1,6-β1= 4,4; |
|
β8=l8,2-α2=2,5; |
α4=l4,4-β4=-2,6; |
|
β5=l5,6-α6=2,5; |
|
β2=l2,3-α3=7,0; |
α1=l4,1-β4=-2,5; |
|
|
и |
α5=l2,5-β2=-3,5; |
β6=l6,1-α1=8,7. |
|
α2=l5,2-β5= -0,2; |
|
|||
α3=l5,3-β5= 2,5; |
|
β3=l3,3-α3=4,7; |
|
|
С |
|
|
|
|
33
|
Значения потенциалов Si,j=li,j-(βi+αj) для всех свободных клеток: |
|||||||||||||||||
S1,1 = l1,1 – (β1+α1)=10,4; |
|
S3,5 = l3,5 – (β3+α5)=4,6; |
S6,6 = l6,6 – (β6+α6)=2,1; |
|||||||||||||||
S1,2 = l1,2 – (β1+α2)=6,3; |
|
S3,6 = l3,6 – (β3+α6)=3,5; |
S7,1 = l7,1 – (β7+α1)=2,8; |
|||||||||||||||
S1,3 = l1,3 – (β1+α3)=2,2; |
|
S4,2 = l4,2 – (β4+α2)=2,9; |
S7,2 = l7,2 – (β7+α2)=10,0; |
|||||||||||||||
S1,4 = l1,4 – (β1+α4)=13,0; |
|
S4,5 = l4,5 – (β4+α5)=5,9; |
S7,4 = l7,4 – (β7+α4)=7,4; |
|||||||||||||||
S1,5 = l1,5 – (β1+α5)=6,5; |
|
S4,6 = l4,6 – (β4+α6)=2,1; |
S7,5 = l7,5 – (β7+α5)=5,9; |
|||||||||||||||
S2,1 = l2,1 – (β2+α1)=0,0; |
|
S5,1 = l5,1 – (β5+α1)=10,0; |
S7,6 = l7,6 – (β7+α6)=5,4; |
|||||||||||||||
S2,2 = l2,2 – (β2+α2)=5,5; |
|
S5,4 = l5,4 – (β5+α4)=9,9; |
S8,1 = l8,1 – (β8+α1)=7,5; |
|||||||||||||||
S2,4 = l2,4 – (β2+α4)=1,8; |
|
S5,5 = l5,5 – (β5+α5)=7,7; |
S8,3 = l8,3 – (β8+α3)=4,6; |
|||||||||||||||
S2,6 = l2,6 – (β2+α6)=4,6; |
|
S6,2 = l6,2 – (β6+α3)=2,9; |
S8,4 = l8,4 – (β8+α4)=7,5; |
|||||||||||||||
S3,1 = l3,1 – (β3+α1)=2,8; |
|
S6,3 = l6,3 – (β6+α3)=0,0; |
S8,5 = l8,5 – (β8+α5)=12,3; |
|||||||||||||||
S3,2 = l3,2 – (β3+α2)=10,0; |
|
S6,4 = l6,4 – (β6+α4)=0,0; |
S8,6 = l8,6 – (β8+α6)= –0,8. |
|||||||||||||||
S3,4 = l3,4 – (β3+α4)=7,4; |
|
S6,5 = l6,5 – (β6+α5)=6,4; |
|
|
|
|
|
|||||||||||
|
Если имеется несколько клеток с одним и тем же наименьшим значением |
|||||||||||||||||
оценки, то из них выбирается клетка, имеющая наименьший потенциал. |
||||||||||||||||||
Наиболее |
потенциальной |
является |
клетка |
Б8А6, для которой |
значение |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
|||
потенциала составляет (–0,8). Для этой клетки и строитсяконтур (табл. 4.9). |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.9 |
|
|
|
Проверка оптимальности опорного плана методом МОДИ |
|
|||||||||||||||
|
|
|
и перераспределение загрузок по контуру |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
ГО |
Д |
|
|
||||||
|
|
|
А1 |
|
|
|
|
|
|
|
|
|
|
А6 |
Объем |
|||
|
|
|
|
|
|
2 |
|
|
3 |
|
|
4 |
|
5 |
||||
ГП |
|
|
|
|
|
|
|
|
|
|
спроса, |
|||||||
|
αi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
βj |
-2,5 |
|
-0,2 |
2,5 |
-2,6 |
-3,5 |
4,4 |
т |
|||||||||
|
|
|
||||||||||||||||
|
|
10,4 |
7,9 |
6,3 |
|
6,1 |
2,2 |
4,7 |
13,0 |
10,4 |
6,5 |
3,0 |
|
4,4 |
|
|||
|
|
|
|
|
|
|||||||||||||
Б1 |
|
0 |
|
|
|
|
|
А |
|
|
140 |
140 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б2 |
|
7,0 |
0,0 |
4,5 |
5,5 |
12,3 |
|
9,5 |
1,8 |
|
6,2 |
|
3,5 |
4,6 |
16,0 |
190 |
||
|
|
|
|
|
|
|
40 |
|
|
|
150 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Б3 |
|
4,7 |
2,8б5,0 10,0 14,5 |
7,2 7,4 9,5 |
4,6 |
5,8 |
3,5 |
12,6 |
120 |
|||||||||
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б4 |
|
4,8 |
|
2,3 |
2,9 |
|
7,5 |
|
7,3 |
|
|
2,2 |
5,9 |
7,2 |
2,1 |
11,3 |
220 |
|
|
40 |
|
|
|
|
15 |
165 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Б5 |
и10,0 10,0+ |
|
2,3 |
|
5,0 |
9,9 |
|
9,8 |
7,7 |
6,7 |
– |
6,9 |
145 |
|||||
|
2,5 |
|
|
|
70 |
15 |
|
|
|
|
|
60 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Б6 |
|
8,7 |
|
6,2 |
2,9 |
11,4 |
0,0 |
11,2 |
0,0 |
|
6,1 |
6,4 |
11,6 |
2,1 |
15,2 |
100 |
||
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б7 |
|
1,1 |
2,8 |
1,4 |
10,0 10,9 |
|
3,6 |
7,4 |
|
5,9 |
5,9 |
3,5 |
5,4 |
10,9 |
150 |
|||
|
|
|
|
|
|
|
150 |
|
|
|
|
|
|
|
||||
С |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
7,5 |
7,5 – |
|
|
2,3 |
4,6 |
9,6 |
7,5 |
|
7,4 |
12,3 11,3 -0,8 |
6,1 |
|
||||||
Б8 |
|
2,5 |
|
|
|
120 |
||||||||||||
|
|
|
|
120 |
|
|
|
|
|
|
|
|
+ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Наличие груза, т |
140 |
|
190 |
340 |
165 |
150 |
200 |
1185 |
||||||||||
|
|
|
|
|
|
|
|
|
|
34 |
|
|
|
|
|
|
|
|
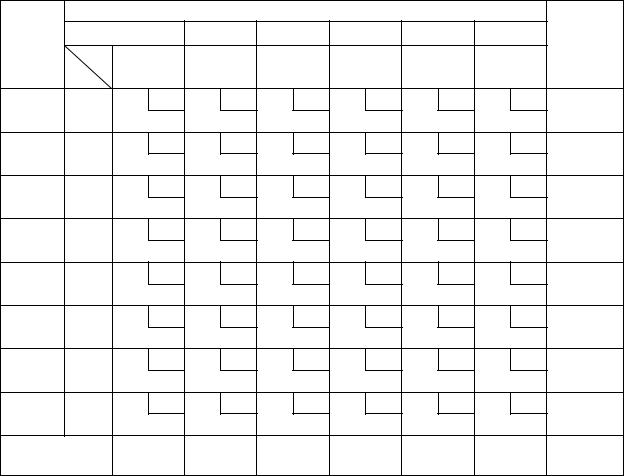
Наименьшее количество груза, находящееся в клетках, отмеченных |
|||||||||||||||||
знаком «–» составляет 60 т (клетка Б5А6), именно это количество и |
|||||||||||||||||
должно быть вычтено из клеток со знаком «–» и прибавлено в клетки со |
|||||||||||||||||
знаком «+». Полученный результат представлен в табл. 4.10. После |
|||||||||||||||||
перераспределения |
|
груза |
вновь |
|
пересчитываются |
значения |
|||||||||||
вспомогательных |
|
индексов |
и |
потенциалов |
незагруженных |
клеток. |
|||||||||||
В данном случае выполненное перераспределение позволило получить |
|||||||||||||||||
оптимальный план, т.к. нет ни одного значения потенциала, для которого |
|||||||||||||||||
выполнялось бы условие, определяемое формулой (4.4). |
|
|
|
||||||||||||||
|
Проверка оптимальности нового плана методом |
|
Таблица 4.10 |
||||||||||||||
|
|
|
|
||||||||||||||
|
|
А1 |
|
А2 |
|
ГО |
А4 |
|
|
|
|
|
|
Объем |
|||
ГП |
|
|
А3 |
А5 |
|
|
А6 |
||||||||||
|
|
|
|
спроса, |
|||||||||||||
αi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
-1,7 |
0,6 |
3,3 |
-1,8 |
-2,7 |
|
4,4 |
т |
|||||||||
|
βj |
|
|||||||||||||||
|
9,6 |
|
7,9 |
5,5 |
6,1 |
1,4 |
4,7 |
12,2 10,4 |
5,7 |
|
3,0 |
|
4,4 |
|
|||
Б |
|
|
|
|
|
||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
МОДИ |
||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
140 |
140 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Б2 |
6,2 |
0,0 |
|
4,5 |
5,5 |
12,3 |
|
9,5 |
1,8 |
6,2 |
|
|
3,5 |
5,4 |
16,0 |
190 |
|
|
|
|
|
|
40 |
|
|
150 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2,8 |
|
5,0 |
10,0 14,5 |
|
7,2 |
7,4 |
9,5 |
4,6 |
|
5,8 |
4,3 |
12,6 |
|
||
Б3 |
3,9 |
|
|
2,3 |
2,9 |
7,5 |
120 |
Д |
11,3 |
120 |
|||||||
Б4 |
4,0 |
|
|
|
7,3 |
|
2,2 |
5,9 |
|
7,2 |
2,9 |
220 |
|||||
40 |
|
|
15 |
165 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
Б5 |
1,7 |
10,0 10,0 |
|
2,3 |
|
5,0 |
9,9 |
9,8 |
7,7 |
|
6,7 |
0,8 |
6,9 |
145 |
|||
|
|
|
|
|
130 |
15 |
|
|
|
|
|
|
|
|
|
||
Б6 |
7,9 |
|
|
6,2 |
2,9 11,4А0,0 11,2 0,0 6,1 |
6,4 |
11,6 |
2,9 |
15,2 |
100 |
|||||||
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Б7 |
0,3 |
2,8 |
|
1,4 |
10,0 10,9 |
|
3,6 |
7,4 |
5,9 |
5,9 |
|
3,5 |
6,2 |
10,9 |
150 |
||
|
|
|
|
|
150 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
7,5 |
б |
7,5 |
7,4 |
12,3 11,3 |
|
6,1 |
|
||||||||
Б8 |
1,7 |
|
7,5 |
|
2,3 |
4,6 |
9,6 |
|
120 |
||||||||
|
|
|
60 |
|
|
|
|
|
|
|
|
60 |
|||||
Нал ч е |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
140 |
190 |
340 |
165 |
150 |
|
200 |
1185 |
||||||||||
груза, т |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ропт = 4987,5 т·км. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Таким образом, опорный план, полученный методом аппроксимации |
|||||||||||||||||
Фогеля, удалось оптимизировать с помощью метода МОДИ. Данная |
|||||||||||||||||
Соптимизация позволила сократить транспортную работу на 48 т·км. |
|||||||||||||||||
35
