Контрольные вопросы и задания
1.Сформулируйте общую задачу линейного программирования.
2.Какая задача называется стандартной задачей линейного программирования?
3.Какая задача называется канонической задачей линейного программирования? И
4.Сформулируйте задачу «Распределение ресурсов».
5.Приведите экономико-математическую модель задачи «Распределение ресурсов».
6.Сформулируйте задачу «О раскрое».
7.Приведите экономико-математическуюДмодель задачи «О раскрое».
8.Сформулируйте задачу «О смесях».
9.Приведите экономико-математическую модель задачи «О смесях».
2.РЕШЕНИЕ ЗАДАЧАЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ГРАФОАНАЛИТИЧЕСКИМ МЕТО ОМб
2. |
Что |
называется градиентом в задачах |
линейного |
|
|
найти |
|
|
|
программ рован я? |
|
|
||
С |
|
ент на графике? |
|
|
3. |
Как постро ть град |
|
||
4. |
Что называется л н ями уровня целевой функции? |
|
||
5. |
Как постро ть л н |
уровня целевой функции на графике? |
||
6. |
Как |
опт мальное решение на графике? |
|
|
7. |
Как |
координаты точки оптимального решения? |
|
|
11
3. РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ СИМПЛЕКСНЫМ МЕТОДОМ
3.1. Пояснительный материал
решаются они по единому алгоритму.
Симплексным методом решают задачи максимизации и минимизации целевой функции. Методики их решенияИразличны, но
Рассмотрим применение симплекс-метода на примере решения
задачи с искусственным базисом на максимум [6].
На предприятие по производству запасных частей для автомобилей поступило три сорта материалов: I – 1200, II – 300, III – 800 кг. Эти материалы могут быть использованы для выпуска запасных частей трех
видов.
На производство запасной части первого вида требуется 5 кг материала I и 4 кг материала II. На производство запасной части второго вида требуется 5 кг материала I и 2 кг материала II, на единицу запасных частей третьего вида необходимо 2 кг материала I, 3 кг – II сорта и 4,8 кг – III сорта. От реализации одной запасной части первого вида предприятие
получает 5 руб. |
, второго – 8 руб., третьего – 6 руб. При этом |
||||
|
прибыли |
|
|
||
следует произвести не менее 20 ед. запасных частей первого вида и не |
|||||
150 ед. запасных частей второго вида. |
Д |
||||
Какое количество запасных частей каждого вида следует |
|||||
производить предприятию, что ы получать максимальную прибыль? |
|||||
означить 1 |
|
|
|
|
|
Если |
ъемы производства запасных частей через x1 , x2 |
||||
и x3 , то можно сформ роватьАмодель следующего вида: |
|||||
С |
F(x)=5x1 +8x2 +6x3 → max , |
||||
при огран чен ях |
|
|
|
|
|
|
x |
≥ 20 |
|
|
|
|
x2 |
≥150 |
|
|
|
|
5x1 +5x2 +2x3 ≤1200, |
||||
|
4x +3x |
3 |
≤ |
300, |
|
|
|
1 |
|
|
|
|
2x2 + 4,8x3 ≤800, |
||||
|
|
|
≥ 0. |
||
|
x1, x2 , x3 |
||||
12
Чтобы приступить к решению данной задачи симплекс-методом, необходимо определить первое допустимое базисное решение. Для этого неравенства преобразуют в равенства путем прибавления в левую часть
неравенств дополнительных переменных x4 и x5 в левую часть первого и второго неравенств с коэффициентом «-1» и переменных x6 , x7, x8,
с коэффициентом, равным «1» в третье, четвертое и пятое неравенства. |
|||||||
|
|
|
|
|
|
И |
|
F(x)=5x1 +8x2 +6x3 +0x4 +0x5 +0x6 → max |
, |
||||||
x |
|
= 20, |
|
|
|
|
|
1 |
|
|
|
|
Д |
|
|
x2 =150, |
|
|
|
|
|||
5x1 +5x2 +2x3 + x4 =1200, |
|
|
|||||
4x |
|
+3x + x = |
300, |
|
|
||
|
1 |
3 |
5 |
|
|
|
|
2x |
|
+4,8x |
+ x |
=800, |
|
|
|
|
|
2 |
А |
|
|
||
|
3 |
6 |
|
|
|
||
x1 |
, x2 , x3, x4 , x5, x6 ≥0. |
|
|
||||
Дополнительные переменные рассматриваются как показатели
способствуют |
|
II и |
||
недоиспользования |
имеющихся |
материалов, соответственно I, |
||
III сортов. Они |
не |
|
увеличению прибыли, |
т.к. |
недоиспользованное сырье не участвует в производстве, поэтому в
формуле целевой функции, определяющей прибыль предприятия, |
|
запасами |
|
записаны с коэффициентами, равными 0. |
|
При решении задачи относительно дополнительных переменных |
|
возможны три случая: |
|
• Дополн тельные переменные равны 0, это |
значит, что при |
про зводстве спользуются все материалы (остатков нет). |
|
С |
т.е. материалы |
• Дополн тельная переменная больше 0, |
|
используются не полностью, имеется остаток, который равен разности между матери лов количеством израсходованных материалов.
• Дополнительная переменная равна запасам материалов, сырье используется не полностью, а основные переменные задачи принимают нулевые значения [6].
В данном случае x4 означает избыток запасных частей первого вида в сравнении с обязательным минимумом (20 ед.), аналогично трактуется
значение x5; x6 , x7, x8 отражают количество недоиспользованных материалов I, II и III сортов соответственно. За базисные переменные можно принять только переменные со знаком «+», т.е. переменные x6 , x7, x8, но всего переменных должно быть 5, поскольку в заданной системе
13
ограничений пять неравенств. Следовательно, их также необходимо ввести. Для этого следует дописать переменные x9, x10 в первое и второе уравнения системы ограничений, а в ц елевую функцию эти переменные войдут с коэффициентом «–М» (где М – очень большое положительное число). Математическая постановка задачи примет вид
F(x)=5x1 +8x2 +6x3 − Мx9 − Мx10 → max
|
|
|
|
x1 − x4 + x9 = 20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
И |
||||||||||||||||||||||||||||||||
|
|
|
|
x |
2 |
− x |
5 |
+ x |
|
=150 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
5x1 +5x2 +2x3 + x6 =1200, |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4x |
|
+3x |
3 |
+ x |
7 |
= 300, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
2x |
2 |
+ |
4,8x |
3 |
+ x |
8 |
= |
800, |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, x5 , x6 |
, x7 , x8 , x9 , x10 |
≥ 0. |
|||||||||||||||||||||||||||||||||
|
|
|
|
x1, x2 , x3 , x4 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Исходная таблица приведена в табл. 3.1. |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
Исходная симплексная таблица |
|
|
|
|
|
|
Таблица 3.1 |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ci |
|
Базисные |
|
|
c j |
|
|
|
5 |
|
|
|
|
8 |
|
|
6 |
|
-М |
-М |
0 |
0 |
0 |
0 |
|
0 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
переменные |
план |
|
|
x1 |
|
|
|
x2 |
|
|
x3 |
|
x4 |
|
|
x5 |
|
x6 |
x7 |
x8 |
x9 |
|
x10 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-М |
|
x9 |
|
|
20 |
|
|
|
1 |
|
|
|
|
|
0 |
|
|
|
0 |
|
|
-1 |
|
0 |
|
|
0 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
-М |
|
x |
|
|
150 |
|
|
|
|
0 |
|
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
-1 |
|
|
|
0 |
|
|
0 |
|
|
0 |
|
|
0 |
|
|
|
0 |
|
||||
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
0 |
|
x6 |
|
1200 |
|
|
5 |
|
|
|
|
|
5 |
|
|
|
2 |
|
0 |
|
|
0 |
|
|
1 |
|
0 |
|
0 |
|
0 |
|
|
0 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
0 |
|
x7 |
|
|
300 |
|
|
|
4 |
|
|
|
|
|
0 |
|
|
|
3 |
|
0 |
|
|
0 |
|
|
0 |
|
1 |
|
0 |
|
0 |
|
|
0 |
|
||||||||||||||
0 |
|
x8 |
|
|
800 |
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
4,8 |
0 |
|
|
0 |
|
|
0 |
|
0 |
|
1 |
|
0 |
|
|
0 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Индексная строка |
|
-170М -5-М |
-8-М |
|
-6 |
|
М |
|
|
М |
|
0 |
|
0 |
0 |
0 |
|
0 |
|||||||||||||||||||||||||||||||||
|
∆j = z j −cj |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Первое |
|
|
|
|
|
решение |
|
|
улучшают |
путем |
|
введения |
в |
него |
||||||||||||||||||||||||||||||||||||
|
|
базисное |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ссоответствует тому, что производство начато, а прибыль предприятия увеличивается за счет включения в него того или иного вида продукции. На каждом этапе анализируется включение в производство только одного вида продукции, что соответствует переходу к новому базису
основных переменных задачи. Значение целевой функции при этом
увеличивается и в кон ечном итоге достигает максимума. Это
(табл. 3.2, 3.3).
14
Поскольку в данном примере стоит задача максимизировать целевую функцию, то решение продолжается до тех пор, пока в строке оценок есть отрицательные элементы; таким образом, необходимо сделать преобразование. Для этого выбираем разрешающий столбец ∆2 = −8 -М и
разрешающую строку 150/1 = 150; 1200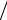
5 = 240; 800
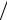2 = 400, на 0 и на
отрицательные числа не делят. Из полученных отношений выбирают наименьшее, т.к. оно определяет количество продукции данного вида, которое можно произвести исходя из ограниченности ресурсов, т.е. узкое место при выпуске данной продукции. Строка с на именьшим отношением и будет разрешающей. Базисную переменную этой строки выводят из решения, заменяя ее переменной разрешающего столбца.
Таблица 3.2
Промежуточная симплексная таблица
|
ci |
|
Базисные |
cj |
5 |
8 |
6 |
|
-М |
-М |
|
0 |
|
0 |
|
0 |
0 |
|
|
0 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
переменные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
план |
|
x |
x |
2 |
|
x |
|
|
x |
4 |
|
|
|
x |
|
|
x |
|
x |
|
|
x |
|
x |
|
x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
1 |
|
3 |
|
|
|
|
|
5 |
|
6 |
|
И7 8 9 |
|
10 |
|||||||||||||||||||||
|
М |
|
x9 |
|
20 |
|
1 |
|
0 |
|
|
0 |
|
|
|
-1 |
|
|
|
0 |
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
1 |
|
0 |
|
|||
|
8 |
|
x2 |
|
150 |
0 |
|
1 |
|
0 |
|
0 |
|
|
-1 |
|
0 |
|
|
0 |
0 |
|
0 |
|
1 |
|
||||||||||||||
|
0 |
|
x6 |
|
450 |
|
5 |
|
0 |
|
2 |
|
0 |
|
|
5 |
|
|
1 |
|
|
0 |
0 |
|
0 |
|
-5 |
|||||||||||||
|
0 |
|
x7 |
|
300 |
|
4 |
|
0 |
|
3 |
|
0 |
|
|
0 |
|
|
0 |
|
|
1 |
0 |
|
0 |
|
0 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
0 |
|
x8 |
|
500 |
|
0 |
|
0 |
|
4,8 |
0 |
|
|
2 |
|
0 |
|
|
0 |
1 |
|
0 |
|
-2 |
|||||||||||||||
|
Индексная строка |
|
1200- |
-5-M |
0 |
|
-6 |
|
|
M -8 |
0 |
|
|
0 |
0 |
0 |
|
8+М |
||||||||||||||||||||||
|
|
∆j = z j −cj |
|
-20М |
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Поскольку в та л. 3.2 еще остались отрицательные элементы, то |
||||||||||||||||||||||||||||||||||||||
|
полученное решен е не опт мально. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3.3 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Окончательная симплексная таблица |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
ci |
|
Баз сные |
c j |
5 |
8 |
6 |
|
|
-М |
-М |
|
0 |
|
0 |
|
0 |
0 |
|
|
0 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
переменные |
план |
|
x1 |
x2 |
|
x3 |
|
|
x4 |
|
|
x5 |
|
|
x6 |
|
|
x7 |
|
|
x8 |
|
x9 |
|
|
x10 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
5 |
|
x1 |
|
20 |
1 |
|
0 |
|
0 |
|
|
-1 |
|
|
0 |
|
|
0 |
|
|
0 |
|
0 |
|
1 |
|
0 |
|
|||||||||||
|
8 |
|
x2 |
|
190,67 |
0 |
|
1 |
|
0 |
|
|
0,47 |
|
0 |
|
|
0,2 |
|
-0,13 |
|
0 |
|
-0,47 |
|
0 |
|
|||||||||||||
|
0 |
|
x5 |
|
40,67 |
0 |
|
0 |
|
0 |
|
|
0,47 |
|
1 |
|
|
0,2 |
|
-0,13 |
|
0 |
|
-0,47 |
|
-1 |
||||||||||||||
|
6 |
|
x3 |
|
73,33 |
0 |
|
0 |
|
1 |
|
|
1,33 |
|
0 |
|
|
0 |
|
|
0,33 |
|
0 |
|
-1,33 |
|
0 |
|
||||||||||||
|
|
|
x |
|
66,68 |
0 |
|
0 |
|
0 |
|
|
-7,33 |
|
0 |
|
|
-0,4 |
|
-1,33 |
|
1 |
|
7,33 |
|
0 |
|
|||||||||||||
|
С0 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Индексная строка |
|
2065,3 |
0 |
|
0 |
0 |
|
6,73 |
|
0 |
|
|
1,6 |
|
0,93 |
|
0 |
|
М- |
|
М |
||||||||||||||||||
|
|
∆j = z j −cj |
|
|
|
|
|
|
|
|
|
-6,7 |
|
|||||||||||||||||||||||||||
15
В табл. 3.3 в строке оценок нет отрицательных элементов, следовательно, найден оптимальный план производства: x1 = 20; x2 = 190,67; x3 = 73,33; x4 = 0; x5 = 40,67; x6 = 0; x7 = 0; x8 = 66,68. Таким образом, чтобы получить максимальную прибыль в размере 2065,3 руб., с соблюдением ограничений по минимальному выпуску запасных частей первого и второго видов, предприятие должно производить 20 ед., запасных частей первого вида, 191 ед. запасных частей второго вида и 73 ед. запасных частей третьего вида.
Оценки индексной строки для основных переменных, не вошедших в оптимальный план, показывают, сколько прибыли пришлось бы потерять предприятию, если бы была произведена единица продукции соответствующего вида. Для дополнительных переменных эти оценки показывают, сколько единиц прибыли приносит единица материалов
данного вида при производстве продукции [6]. |
|
3.2. Решение задач линейного программирования |
|
с применением MS Excel |
И |
|
|
В MS Excel существует возможность с помощью надстройки Поиск решения («в исходной версии Solver – Решатель» [8]) найти решение
задач оптимизации, в том числе задач линейного программирования. |
|
Чтобы запустить надстройку ПоискДрешения, необходимо в главном |
|
меню выполнить операцию Сервис | Поиск решения. Если в меню Сервис |
|
отсутствует |
Поиск решения, следует выбрать операцию |
Надстройки в том же меню Сервис: Сервис | Надстройки и установить
флажок По ск решен я. В д диалогового окна Поиск решения приведен |
||
|
|
А |
на р с. 3.1, оп сан е элементов которого приведено в табл. 3.4. |
||
|
б |
|
операция |
|
|
С |
|
|
Рис. 3.1. Окно Поиск решения
16
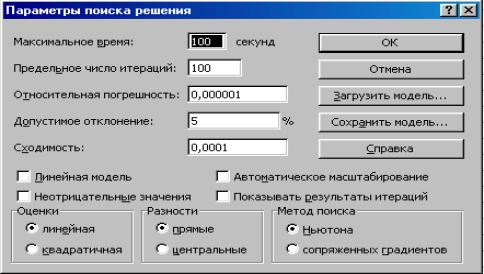
При нажатии кнопки Параметры в окне Поиск решения открывается окно Параметры поиска решения (рис. 3.2), описание элементов которого приведено в табл. 3.5.
|
|
|
Таблица 3.4 |
|
|
|
|
Описание элементов окна Поиск решения |
|
|
|
|
|
|
|
|
Элементы |
Описание |
|
|
|
|
СибАДИ |
|
|
|
Установить |
«Используется для задания ссылки на ячейку, в которой задана |
|
|
|
целевую ячейку |
формула с выражением целевой функции решаемой задачи |
|
|
|
|
оптимизации» [9] |
|
|
|
Равной |
«Определяют характер решаемой задачи оптимизации. Для |
|
|
|
|
нахождения решения с максимальным значением целевой |
|
|
|
|
функции этот переключатель ставится в положение |
|
|
|
|
Максимальному значению, для нахождения решения с |
|
|
|
|
минимальным значением – в положение Минимальному |
|
|
|
|
значению. Наконец, для нахождения решения, при котором |
|
|
|
|
целевая функция принимает некоторое фиксированное значение, |
|
|
|
|
переключатель ставится в положение Значению, справа от |
|
|
|
|
которого можно ввести требуемое фиксированное значение» [9] |
|
|
|
Изменяя ячейки |
«Служит для указания ячеек, которые должны изменяться в |
|
|
|
|
процессе поиска решения задачи. Именно в этих ячейках должны |
|
|
|
|
находиться переменные решаемой задачи оптимизации» [9] |
|
|
|
Ограничения |
«Отображаются ограничения решаемой задачи оптимизации» [9] |
|
|
|
Кнопка Добавить |
«Служит для вызова дополнительного окна Добавление |
|
|
|
|
ограничения» [9] |
|
|
|
Кнопка |
«Служит для вызова дополнительного окна Параметры поиска |
|
|
|
Параметры |
решения (рис. 1.2) для спецификации дополнительных |
|
|
|
|
параметров поиска решения, часть которых уже задана по |
|
|
|
|
умолчан ю» [9] |
|
|
|
|
|
|
|
|
|
Рис. 3.2. Окно Параметры поиска решения |
|
17
Таблица 3.5
Описание элементов окна Параметры поиска решения
|
|
Элементы |
|
|
|
|
Описание |
|
||
|
Максимальное время |
«Служит для ограничения времени, отпускаемого на |
||||||||
|
|
|
|
|
поиск решения задачи» [9] |
|
|
|||
|
Предельное |
|
число |
«Служит |
для ограничения времени решения задачи |
|||||
|
итераций |
|
|
посредством задания некоторого предельного числа |
||||||
|
|
|
|
|
промежуточных вычислений» [9] |
|
||||
|
Относительная |
|
|
«Служит для задания точности, с которой будет |
||||||
|
погрешность |
|
|
выполняться поиск решения. В отдельных случаях |
||||||
|
Допустимое отклонение |
целесообразно после нахождения решения со значениями |
||||||||
|
|
|
|
|
этих параметров, заданными по умолчанию, повторить |
|||||
|
|
|
|
|
вычисления с большей точностью и меньшим |
|||||
|
|
|
|
|
допустимым отклонением. После выполнения поиска |
|||||
|
|
|
|
|
решения сравнить полученные результаты» [9] |
|||||
|
Линейная модель |
|
«Служит для ускорения поиска решения задачи |
|||||||
|
|
|
|
|
оптимизации с линейной целевой функцией и линейными |
|||||
|
|
|
|
|
ограничениями. ля задач нелинейной оптимизации этот |
|||||
|
|
|
|
|
флажок должен быть сброшен, аИдля задач линейного |
|||||
|
|
|
|
|
программирования установлен, поскольку в противном |
|||||
|
|
|
|
|
случае возможно получение неверного результата» [9] |
|||||
|
Показывать |
результаты |
«Служит |
для приостановки поиска решения для |
||||||
|
итераций |
|
|
просмотра результатов отдельных итераций» [9] |
||||||
|
|
|
Д |
|||||||
|
Автоматическое |
|
«Служит для включения автоматической нормализации |
|||||||
|
масштабирование |
|
входных |
и |
выходных |
значений, |
качественно |
|||
|
|
|
|
|
различающихся по величине. Например, при |
|||||
|
|
|
|
|
максимизации прибыли в процентах по отношению к |
|||||
|
|
|
|
|
вложениям, исчисляемым в миллионах рублей» [9] |
|||||
|
Оценки |
|
|
|
Группа служит «для указания метода экстраполяции |
|||||
|
|
|
|
|
|
А |
|
|
||
|
|
|
|
|
(л нейная или квадратичная)» [9] |
|
||||
|
Разности |
|
|
Группа |
служит |
для «указания метода |
численного |
|||
|
|
|
|
|
д фференцирования» [9] |
|
|
|||
|
Метод по ска |
|
|
Группа служит «для выбора алгоритма оптимизации» [9] |
||||||
|
|
|
|
б |
|
|
|
|||
|
Кнопки |
охран ть модель и Загрузить модель окна Параметры |
||||||||
|
поиска |
|
|
позволяют |
задать ссылку на ячейки, содержащие |
|||||
|
загружаемую |
модель |
|
сохранить на листе более одной модели |
||||||
|
|
решения |
|
|
|
|
|
|||
|
оптимизации [9]. |
|
|
|
|
|
|
|
||
|
|
Решение задачи с помощью надстройки Поиск решения |
||||||||
СРешение задачи с помощью надстройки Поиск решения |
||||||||||
|
рассмотрено на примере, приведенном в подр. 3.1. |
|
|
|||||||
18
Решение [8, 9, 13]:
1. Сформулирована математическая модель задачи:
F(x)= 5x1 +8x2 +6x3 → max ,
x |
≥ 20 |
|
|
|
|
1 |
≥150 |
|
|
|
|
x2 |
|
|
|
||
5x1 +5x2 + 2x3 ≤1200, |
|
||||
4x +3x |
3 |
≤ 300, |
|
||
|
1 |
|
Д |
||
2x2 + 4,8x3 ≤800, |
|
||||
|
|
≥ 0. |
|
|
|
x1, x2 , x3 |
|
|
|||
2. Подготовка листа рабочей книги MS Excel для вычислений – на |
|||||
|
А |
|
|||
рабочий лист вводят необходимый текст, данные и формулы в |
|||||
соответствии с рис. 3.3. |
|
|
|
|
И |
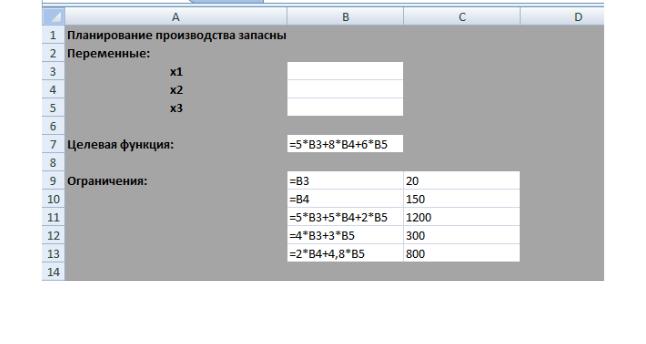
Переменные задачи x1, x2 и x3 находятся, соответственно, в ячейках |
|||||
B3, B4 и B5. Целевая функция находится в ячейке B6 и содержит фор- |
|||||
б |
|
|
|||
мулу = 5·B3+8·B4+6·B5.Ограничения на задачу учтены в ячейках B9:C14.
3. Работа с надстройкой Поиск решения
– воспользовавшись операцией Сервис | Поиск решения, вводят необходимые данные для рассматриваемой задачи (установка данных в
рис |
|
окне Поиск решения приведена на рис. 3.4. Результат работы надстройки |
|
приведен на |
. 3.5. |
С
Рис. 3.3. Рабочий лист MS Excel для решения задачи планирования производства материалов
19