
- •ВВЕДЕНИЕ
- •Раздел 1. ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ
- •1.1. Понятие о системах счисления. Основные определения
- •1.2. Представление чисел в позиционных системах счисления
- •1.3.1. Перевод целых чисел
- •1.3.2. Перевод дробных чисел
- •1.3.3. Перевод смешанных чисел
- •1.4. Арифметические операции в позиционных системах счисления
- •1.4.1. Сложение в двоичной системе счисления
- •1.4.2. Вычитание в двоичной системе счисления
- •1.4.3. Умножение в двоичной системе счисления
- •1.4.4. Деление в двоичной системе счисления
- •Самостоятельная работа
- •Раздел 2. ИЗМЕРЕНИЕ ИНФОРМАЦИИ
- •2.1. Понятия и основные свойства информации
- •2.2. Единицы измерения информации
- •2.3. Основные подходы к измерению информации
- •2.3.1. Алфавитный подход к измерению информации
- •2.3.2. Содержательный подход к измерению информации
- •Самостоятельная работа
- •Раздел 3. ОСНОВЫ ЛОГИКИ И ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА
- •3.1. Алгебра высказываний. Логические выражения и таблицы истинности
- •3.1.1. Конъюнкция (логическое умножение)
- •3.1.2. Дизъюнкция (логическое сложение)
- •3.1.3. Инверсия (логическое отрицание)
- •3.1.5. Операция логического равенства (эквивалентность)
- •3.2. Логические формулы
- •3.3. Логические схемы
- •Самостоятельная работа
- •Раздел 4. ОСНОВЫ АЛГОРИТМИЗАЦИИ
- •4.1. Понятие алгоритма
- •4.2. Свойства алгоритмов
- •4.3. Форма записи алгоритмов
- •4.3.3. Программный способ записи алгоритмов
- •4.3.4. Псевдокоды
- •4.4.1. Алгоритмическая структура «Следование»
- •4.4.3. Алгоритмическая структура «Выбор»
- •4.4.4. Алгоритмическая структура «Цикл»
- •Самостоятельная работа
- •Библиографический список
Процесс разработки алгоритма называется алгоритмизацией. Процесс разработки сложной задачи требует квалификации, четкого и
полного |
понимания |
задачи. |
Сущность |
алгоритмизации |
вычислительного процесса проявляется в следующих действиях: |
||||
- выделение законченных частей вычислительного процесса; |
||||
С |
|
|
|
|
- |
формальная запись каждого из них; |
|
||
- назначение определенного порядка выполнения выделенных |
||||
частей; |
|
|
|
|
- |
проверка прав |
льности выбранного алгоритма. |
||
и |
|
|
||
Алгор тм, зап санный на «понятном» компьютеру языке |
||||
программ рован я, называется программой [4]. |
|
|||
|
|
4.2. Свойства алгоритмов |
|
|
|
бА |
|
||
Основные свойства алгоритмов следующие: |
|
|||
Понятность для |
сполнителя – исполнитель алгоритма должен |
|||
знать, как его выполнять. |
|
|
||
Д скретность (прерывность, раздельность) – алгоритм должен |
||||
представлять процесс решения задачи как последовательное |
||||
выполнение простых (или ранее определенных) шагов (этапов). |
||||
Определенность – каждое правило алгоритма должно быть |
||||
четким, |
однозначным. |
Благодаря |
этому свойству выполнение |
|
алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задачи.
Результативность (или конечность) состоит в том, что алгоритм должен приводить к решению задачи за конечное число
шагов.
Д Массовость означает, что алгоритмИрешения задачи
разрабатывается в общем виде, т.е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма [6].
4.3. Форма записи алгоритмов
На практике наиболее распространены следующие формы представления алгоритмов:
словесная (запись на естественном языке);
графическая (изображения из графических символов);
59
программная (тексты на языках программирования); псевдокоды (полуформализованные описания алгоритмов на
условном алгоритмическом языке, включающие как элементы языка программирования, так и фразы естественного языка, общепринятые математические обозначения и др.) [4].
С4.3.1.Словесный способ записи алгоритмов
Этот способ зап си алгоритмов представляет собой описание последовательныхеслиэтапов обработки данных. Алгоритм задается в произвольном зложен и на естественном языке.
Напр мер, алгор тм для решения квадратного уравнения ax2 bx c 0 выглядит следующим образом:
4)еслибАзначен е дискриминанта равно нулю, то вычислить х1 и вывести на экран его значение;
5)если же значение дискриминанта получилось меньше нуля необходимо выдать на экран сообщение: « ействительных корней
нет».
Описанный алгоритм применимДк любым числам и должен приводить к решению поставленной задачи.
Словесный способ не имеет широкого распространения, так как такие описания строго не формализуемы; страдают многословностью
записей; допускают неоднозначность толкования отдельных предписаний [4]. И
При графическом представлении алгоритм изображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий.
Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий
60
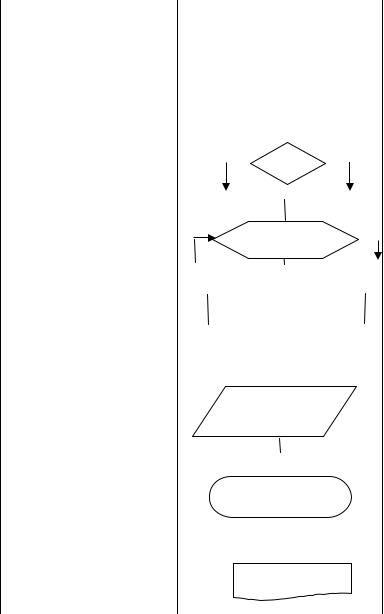
соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. В табл. 3 приведены наиболее часто употребляемые символы [4].
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 3 |
|
|
|
Условные обозначения действий в блок-схеме |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Назван е |
|
Обозначение и пример |
Пояснение |
|
||||||||
|
|
|
заполнения |
|
|||||||||
|
|
|
|
|
|
|
|||||||
|
Процесс |
|
|
|
|
|
|
|
|
|
|
Вычислительное действие или |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
X=a+b/3 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
С |
|
|
|
|
|
|
|
|
|
последовательность действий |
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
да |
|
|
нет |
Проверка условий |
|
|||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||
|
Решение a<b |
|
|
|
|
|
|||||||
|
|
|
|
|
|||||||||
|
Модиф кац я |
|
|
|
I=1, 30, 2 |
Начало цикла |
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предопределенный |
|
|
|
|
|
|
|
|
|
Вычисления по |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Расчет параметров |
|
|
|||||||||
|
|
|
подпрограмме, стандартной |
|
|||||||||
|
процесс |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
подпрограмме |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бА |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ввод-вывод |
|
|
|
|
Ввод |
Ввод-вывод в общем виде |
|
|||||
|
|
|
|
|
a, b, c |
|
|||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
Д |
|
|||||
|
Пуск-останов |
|
|
|
Начало Начало, конец алгоритма, |
||||||||
|
|
|
|
|
|
|
|
|
|
вход и выход в подпрограмму |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Документ |
|
|
|
|
Печать а |
Вывод результатов на печать |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
И |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.3.3. Программный способ записи алгоритмов
При записи алгоритма в словесной форме, в виде блок-схемы или на псевдокоде допускается определенный произвол при изображении команд. Вместе с тем такая запись точна настолько, что
61
позволяет человеку понять суть дела и исполнить алгоритм.
На практике в качестве исполнителей используются
компьютеры. Поэтому алгоритм, предназначенный для исполнения на |
||||||||
компьютере, должен быть записан на понятном ему языке. Здесь на |
||||||||
первый план выдвигается необходимость точной записи команд, не |
||||||||
С |
|
|
|
|
|
|
|
|
оставляющей места для произвольного толкования их исполнителем. |
||||||||
ледовательно, язык для записи алгоритмов должен быть |
||||||||
формал зован. |
Такой |
язык |
принято |
называть |
языком |
|||
программ рован я, а запись алгоритма на этом языке – программой |
||||||||
для компьютера. |
|
|
|
|
|
|
|
|
|
|
4.3.4. Псевдокоды |
|
|
|
|
||
Псевдокод представляет со ой систему обозначений и правил, |
||||||||
предназначенную |
для |
единоо разной |
записи |
алгоритмов. |
В |
|||
псевдокодеине пр няты строгие синтаксические правила для записи |
||||||||
команд, пр сущ е формальным языкам, что облегчает запись |
||||||||
алгоритма на стад |
его проектирования и дает возможность |
|||||||
использовать |
широкий |
набор |
команд, |
|
рассчитанный |
на |
||
более абстрактного исполнителяА.
Однако в псевдокоде есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.
Единого определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций. Примером псевдокода
является школьный алгоритмический язык. |
И |
4.4. Основные типыДалгоритмических структур
Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых элементов. Для их описания следует использовать язык схем алгоритмов и школьный алгоритмический язык.
Логическая структура любого алгоритма может быть представлена комбинацией трех базовых структур: «Следование», «Ветвление», «Цикл». Характерной особенностью базовых структур является наличие в них одного входа и одного выхода.
62
