
1458
.pdf-
(-1; j0)
, . ,
W ( j ) |
B( j ) |
1, |
(3.33) |
|
|||
|
A( j ) |
|
|
D (p) = A(p) + B(p) = 0 , ,
(0 ± ),
.
.
, , , , ,
.
3.8.
, ,
.
,
,
, , , -
– ( . 3.5). , -
| – |.
,
– m/2 -
– . m -
-
.
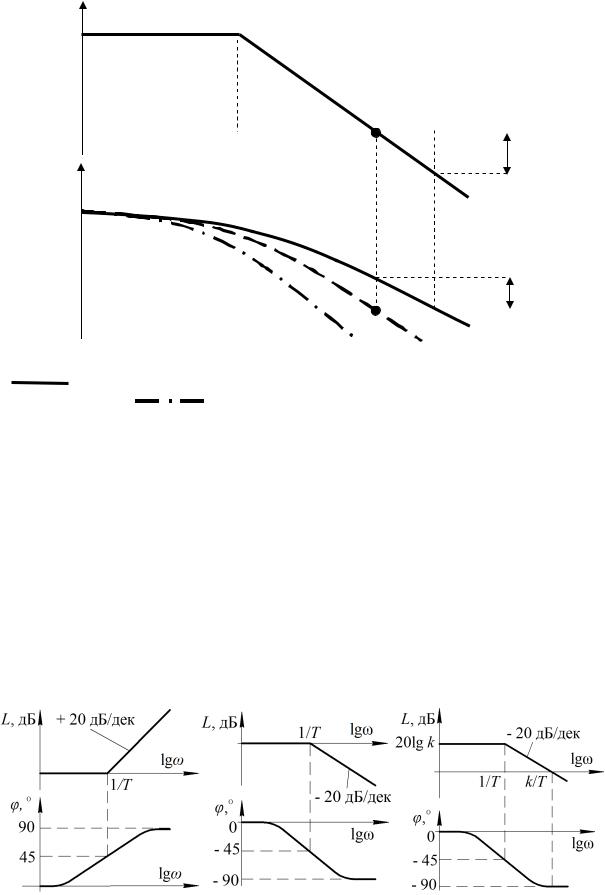
L – -
,
.
–
, -
.
70
L,
lg
0 
0 |
|
L |
,
0  lg
lg
– 
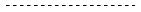
. 3.5. :
– , 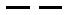 – ,
– ,
–
-
, ( ) ( ) 2.11.
, -
( . . 3.2).
3.2
W ( p) (Tp 1) |
W ( p ) |
1 |
|
W ( p) |
k |
|
(Tp 1) |
|
(Tp 1) |
|
|||
|
|
|
|
|
||
|
|
|
|
|
|
|
71
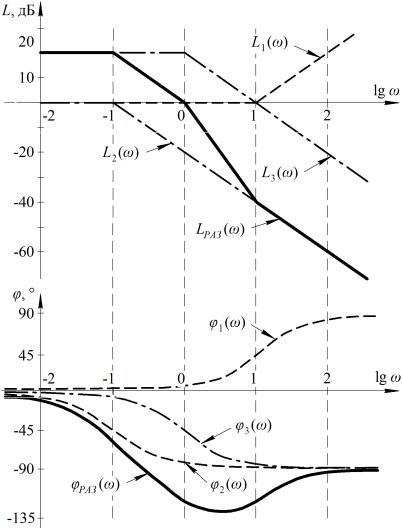
-
( . 3.6):
L ( ) L1( ) L2 ( ) L3 ( ) ; |
(3.34) |
( ) 1( ) 2 ( ) 3 ( ) . |
(3.35) |
, , .
A
U( ) (-1; j0) ( . 3.7).
U( ) , -
1.
. 3.6.
72
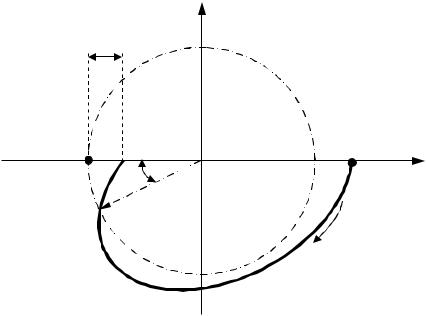
jV( )
-1 |
0 |
|
U( ) |
|
|
. 3.7.
,
.
, -
.
-
: L 6 30 .
-
.
, -
.
3.9.
, -
, -
.
, , -
,
( . . 1.2),
( . . 2.5):
73
x x1 , x2 ... xn T . |
(3.36) |
, –
( ),
(2.32 2.33).
–
,
.
-
.
,
u(t),
x(t0)
x(tK) (t0 – tK). , -
, u(t)
xi(t).
,
, , -
. .
n ( n -
), m k , -
x Ax Bu; |
(3.37) |
|
|
y Cx Du. |
|
,
K , . .
n.
K
:
K B, AB, A2 B,..., An 1B . |
(3.38) |
, = 0,
, u(t) -
y(t).
-
, , -
.
74
–
, -
, . ,
, -, .
,
y(tK) (t0 – tK)
u(t)
x(t0), . .
xi(t) -
y(t).
xi(t) -
x, -
, .
, -
K , . . -
n.
K
:
C
CA
K |
|
|
CA2 |
. |
(3.39) |
|
|
|
|
|
|
|
|
|
|
... |
|
|
||
|
|
|
|
n 1 |
|
|
|
|
CA |
|
|
|
|
, = 0,
, -
y(t). -
, -
,
,
( ) .
,
. 3.8.
75

u |
|
1 T1 p |
|
1 |
|
|
||
|
|
1 T2 p |
|
|
|
1 T3 p |
|
|
. 3.8.
-
T T p2 y T p y T p y y T p u u . |
(3.40) |
||||
2 |
3 |
2 |
3 |
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
||
x |
|
|
|
x |
u; |
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||
1 |
|
T2 |
1 |
|
|
T2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x2 |
|
|
|
|
x2 |
|
|
|
|
u; |
|
. |
(3.41) |
||||
T3 |
|
|
T3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
T2 T1 |
|
|
|
|
|
T3 T1 |
|
|
|||||||
y |
x |
x . |
|
||||||||||||||
|
|
|
|||||||||||||||
|
|
T |
|
T |
|
|
1 |
|
|
T |
T 2 |
|
|||||
|
2 |
|
3 |
|
|
|
|
|
|
3 |
2 |
|
|
||||
, (3.41), -
. 3.9.
|
1 |
|
|
1 |
|
T2 T1 |
|
|
||||||
|
|
|
T2 1 T2 p |
|
|
|
T2 T3 |
|
|
+ |
||||
u |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
1 |
|
|
2 |
|
|
T3 T1 |
|
|||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
T3 1 T3 p |
|
|
|
|
T3 T2 |
|
|
|
||
. 3.9.
T3 T1 2
y(t), . .
.
( )
, ,
T3 T1 .
76

,
.
3.10.
: -
-
.
, -
, -
, -
( , -
,
).
– ,
.
, -
. 3.10.
u |
|
|
K1 |
|
|
K2 |
|
|
K3 |
|
|||
|
- |
|
T1 p 1 |
|
|
|
T2 p |
|
|
|
T3 p |
|
|
. 3.10.
( . . 2.12)
W |
( p) |
K 1 K 2 |
K 3 |
. |
(3.42) |
|
(T1 p 1) T2 p T3 p |
||||||
|
|
|
|
|||
, -
,
W ( p) |
K1K2 K3 |
. |
(3.43) |
|
(T1 p 1) T2 p T3 p K1K2 K3 |
||||
|
|
|
77

(3.43)
( . . 3.5)
|
|
|
|
|
|
T T |
T |
3 |
p 3 |
T |
T |
3 |
p 2 0 p K |
1 |
K |
2 |
K |
3 |
|
0 . |
|
|
|
(3.44) |
|||||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
, - |
||||||||||||||||||||||||||||||||||||||
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
T T |
|
|
|
|
K K |
|
K |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
|
1 |
2 |
|
3 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.45) |
|
|
|
|
|
|
|
|
|
T1T2T3 |
|
|
0 |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
T T |
|
|
K K |
2 |
K |
3 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 T2T3 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.46) |
||||||
|
|
|
|
|
|
|
|
|
|
T2T3 |
K1K2K3 |
|
T T T K K |
|
K |
|
; |
|
|
|
(3.47) |
||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
2 |
3 |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
T1T2T3 |
|
|
|
|
|
0 |
|
|
|
1 |
2 |
3 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
T2T3 |
|
K1K2K3 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)2 |
T T T . (3.48) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
3 |
|
T T T |
0 |
|
|
|
|
|
0 |
|
|
|
K K |
K |
3 |
|
2 |
(K K |
2 |
K |
||||||||||||||||||||
|
|
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
3 |
|
1 |
2 |
3 |
||||
|
|
|
|
0 |
|
T2T3 |
|
|
|
K1K2K3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
, -
T K -
, ,
. , -
.
, -
. 3.11.
u |
|
|
|
K1 |
|
|
K2 |
|
|
K3 |
|
|
|||
|
- |
|
|
T1 p 1 |
|
|
|
T2 p 1 |
|
|
|
T3 p 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. 3.11.
78
( . . 2.12)
W ( p) |
K1 K 2 K 3 |
. |
(3.49) |
|
(T1 p 1)(T2 p 1)(T3 p 1) |
||||
|
|
|
, -
,
W ( p) |
K1K2K3 |
, |
(3.50) |
|
(T1 p 1)(T2 p 1)(T3 p 1) K1K2K3 |
||||
|
|
|
(3.50)
( . . 3.5)
T T T p3 |
(T T T T T T ) p2 |
(T T T ) p K K |
2 |
K |
3 |
1 0 . (3.51) |
||||||||||
1 |
2 |
3 |
1 |
2 |
2 |
3 |
1 |
3 |
1 |
2 |
3 |
1 |
|
|
||
, -
:
|
T T T T T T |
K K |
|
K |
|
1 |
|
|
0 |
|
||||||||||
|
|
1 |
2 |
|
|
2 |
3 |
1 |
3 |
1 |
2 |
|
3 |
|
|
|
0 |
|
||
|
|
|
|
T1T2T3 |
|
|
T1 T2 T3 |
|
|
. (3.52) |
||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
T1T2 T2T3 T1T3 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
K1K2 K3 1 |
||||||||||
: |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
1 T1T2 T2T3 T1T3 ; |
|
|
|
(3.53) |
|||||||
|
|
|
|
|
|
2 |
|
|
T1T2 T2T3 T1T3 |
|
K1K2K3 1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
T1T2T3 |
|
T1 T2 T3 |
|
|
(3.54) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(T1T2 T2T3 T1T3 ) (T1 T2 T3 ) T1T2T3 (K1K2 K3 1); |
||||||||||||||||||||
|
|
T1T2 T2T3 T1T3 |
K1K2 K3 1 |
|
|
0 |
|
|||||||||||||
|
|
|
|
|
||||||||||||||||
3 |
|
|
|
|
T1T2T3 |
|
|
T1 T2 T3 |
|
|
0 |
|
||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
T1T2 T2T3 T1T3 |
K1K2 K3 1 |
(3.55) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
(K1K2 K3 1) 2.
, -
T K
, ,
. , -
.
79
