
1458
.pdf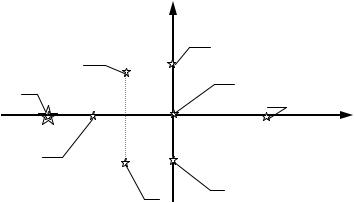
(
, ).
.
, -
.
3.2.
|
B( p) |
|
b pm b pm 1 |
b pm 2 |
... b |
|
|||||
W ( p) |
|
|
0 |
1 |
2 |
|
|
m |
, |
(3.3) |
|
A( p) |
a pn a pn 1 |
|
pn 2 |
... a |
|
||||||
|
|
a |
2 |
n |
|
||||||
|
|
0 |
1 |
|
|
|
|
||||
B(p) = b0 pm + b1 pm-1 + b2 pm-2 + … + bm – ,(p) = a0 pn + a1 pn-1 + a2 pn-2 + … + an – .
, -
, -
, .
(p)
, -
:
a0 pn + a1 pn-1 + a2 pn-2 + … + an = 0. |
(3.4) |
pi
( . 3.1):
|
pi = j = Re(pi) jIm(pi). |
(3.5) |
|
Im |
|
|
5 |
|
|
4 |
|
6 |
3 |
|
1 |
|
|
|
|
|
|
0 |
Re |
|
2 |
|
4 |
5 |
|
. 3.1.
60

:
:
(1);
(2);
(3);
:
(4);
(5);
:
(1, 2, 3);
(4, 5): pi = j ;
(6) pi = pi +1 = ….
3.3.
-
-
(3.4).
,
-
, . . < 0 (3.5). -
.
( = 0),
, ,
.
( > 0),
.
W ( p) |
3 p 4 |
|
p 3 2 p 2 2,25 p 1,25 . |
(3.6) |
: p3 + 2p2 + 2,25p + 1,25 = 0.
: p1 = – 1; p2 = – 0,5 + j; p3 = – 0,5 – j.
, ,
.
61

. .
, -
.
(3.6) -
.
3.4.
.
, -
-
:
1)
, -
n:
Ck,1 = a0, a2, a4,… |
(3.7) |
2)
, n–1:
Ck,2 = a1, a3, a5,… |
(3.8) |
3) |
|
(3.4) |
|
Ck,i = Ck+1,i-2 – ri·Ck+1,i-1, |
(3.9) |
|
|
ri = C1,i-2/C1,i-1, |
(3.10) |
i 3 – , k – .
( . 3.1) -
n.
3.1
|
ri |
i \ k |
|
1 |
|
|
2 |
|
|
3 |
4 |
|
– |
1 |
C11 |
= a0 |
|
C21 |
= a2 |
|
C31 |
= a4 |
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
– |
2 |
C12 |
= a1 |
|
C22 |
= a3 |
|
C32 |
= a5 |
... |
|
|
|
|
|
|
|
|
|
|||
r3 |
= C11/C12 |
3 |
C13 = C21 – r3C22 |
C23 |
= C31 – r3C32 |
C33 |
= C41 – r3C42 |
... |
|||
|
|
|
|
|
|
|
|
|
|||
r4 |
= C12/C13 |
4 |
C14 = C22 – r4C23 |
C24 |
= C32 – r4C33 |
C34 |
= C42 – r4C43 |
... |
|||
|
|
|
|
|
|
|
|
|
|||
|
... |
... |
... |
|
... |
|
... |
... |
|||
62
, -
C11, C12, C13,... -
. , , -
.
. -
. – ,
,
.
3.5.
. -
.
,
( . . 2.10)
W |
( p) |
B( p) |
. |
(3.11) |
|
||||
|
|
A( p) |
|
|
,
, ( . . 2.12)
|
|
|
|
B( p) |
|
|
|
|
|
|
W ( p) |
W ( p) |
|
|
A( p) |
|
|
B( p) |
. (3.12) |
||
1 1 W ( p) |
1 |
B( p) |
|
A( p) B( p) |
||||||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
A( p)
, -
W (p):
A(p) + B(p) = d0 pn + d1 pn-1 + ….+ dn-1 p + dn. |
(3.13) |
, -
(3.13).
-
, d1 dn.
63
,
d ,
– . 0
, n .
d1 |
d3 |
d5 |
|
0 |
|
|
|||
|
|
d 2 |
d 4 |
|
0 |
|
|
||
d0 |
|
|
|||||||
|
0 |
d |
1 |
d |
3 |
|
0 |
. |
(3.14) |
|
|
|
|
|
|
|
|
||
|
|
|
|||||||
|
0 |
0 |
0 |
|
|
|
|
||
|
d n |
|
|||||||
,
n -
:
1 d1 0 ; 2 |
|
d1 |
d3 |
0 |
. |
(3.15) |
|
d0 |
d 2 |
||||||
|
|
|
|
|
,
. -
, ,
.
W ( p) |
B( p) |
|
2 p3 9 p 2 6 p 1 |
. |
(3.16) |
||||
A( p) |
2 p 4 |
3 p 3 |
p 2 |
|
|||||
|
|
|
|
||||||
,
, -
-:
A(p) + B(p) = 2p4 + 3p3 + p2 + 2p3 + 9p2 + 6p + 1 = |
|
= 2p4 + 5p3 + 10p2 + 6p + 1. |
(3.17) |
n 4,
4 4.
: d0 = 2, d1 = 5, d2 = 10, d3 = 6, d4 = 1.
64
|
5 |
6 |
0 |
0 |
|
|
|
|
|
|
10 |
1 |
0 |
|
|
|
2 |
|
(3.18) |
||||
|
0 |
5 |
6 |
0 |
. |
||
|
|
|
|
||||
|
|
0 |
2 |
10 |
1 |
|
|
|
|
|
|
||||
:
1 = 5 > 0;
2 |
|
5 6 |
5 10 2 6 38 0 ; |
|||||
|
|
|
|
2 |
10 |
|
|
|
|
|
|
5 |
6 |
0 |
|
(5 10 6 6 1 0 2 5 0) (0 10 0 5 5 1 2 6 6) 209 0 ; |
|
|
|
|
||||||
3 |
|
2 |
10 |
1 |
|
|||
|
|
|
0 |
5 |
6 |
|
|
|
4 = 1 3 = 1 209 > 0.
, -
.
3.6.
,
,
W ( p) |
B( p) |
e p , |
(3.19) |
A( p)
– .
-
.
. . . .
, , -
-
. .
. . -
,
. (3.19), -
65
,
:
A(p) + B(p e- p. |
(3.20) |
D (j ) -
, -
p -
j :
D ( j ) a ( j )n a ( j )n 1 ... a |
|
|||
|
0 |
1 |
|
n |
b ( j )m e j b ( j )m 1 |
e j ... b e j , (3.21) |
|||
0 |
|
1 |
|
m |
j  1 – .
1 – .
-
|
|
e j cos j sin . |
(3.22) |
j ,
(3.21) (3.22)
D ( j ) U D ( ) j VD ( ) ; |
(3.23) |
UD( ) – , -
, j; VD( ) – ,
, j.
, n = 3, m = 2
U |
D |
a 2 |
a |
3 |
b 2 |
cos b |
cos b sin ; |
(3.24) |
|||||||
|
|
1 |
|
|
0 |
|
2 |
1 |
|
|
|||||
V |
D |
a |
3 |
a |
2 |
b cos b |
|
2 sin b |
2 |
sin . |
(3.25) |
||||
|
|
0 |
|
|
1 |
0 |
|
|
|
|
|||||
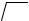
-
[+1; j] D (j ) (3.23) -
0 UD( ) VD( ) – -
( . 3.2).
,
-
[+1; j] -
, n -
, n – -
.
66
-
, -
, .
|
jVD( ) |
|
II |
|
|
|
I |
|
|
|
|
4-
0 |
0 |
UD( ) |
|
|
|
III |
|
IV |
. 3.2.
. ,
, -
. ,
.
3.7.
. -
.
.
[+1; j]
, ( )
( ).
.
( )
, ( ) –
:
A ( ) A1 ( ) A2 ( ) A3 ( ) A4 ( ) ; |
(3.26) |
( ) 1 ( ) 2 ( ) 3 ( ) 4 ( ) . |
(3.27) |
67

( ) ( )
U( ) V( )
W( ) .
,
p . , -
U( ) V( ) ,
, |
- |
|||||||||||||||||
: |
|
|
|
|
|
|
|
|
||||||||||
W ( j ) |
|
K |
|
|
K |
|
|
|
(1 jT ) |
|
K j KT |
|
||||||
1 T j |
(1 jT ) |
|
(1 jT ) |
1 2T 2 |
||||||||||||||
|
|
K |
|
j |
|
|
KT |
|
U ( ) j V ( ) . |
(3.28) |
||||||||
1 2T 2 |
1 2T 2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
( ) |
( ) |
|||||||||||||||||
W( ): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A( ) |
|
U 2 ( ) V 2 ( ) ; |
|
|
(3.29) |
||||||||||
|
|
|
|
( ) arctg |
V ( ) |
. |
|
|
(3.30) |
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
U ( ) |
|
|
|
|||||
U ( ) |
V ( ) |
- |
||||||||||||||||
W ( )
( ) ( ):
U ( ) A ( ) cos ; |
(3.31) |
V ( ) A ( ) sin . |
(3.32) |
,
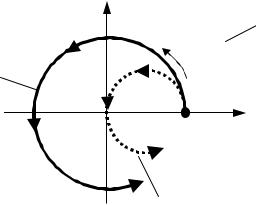
,
[+1; j] ( . 3.3) 0 -
(-1; j0).
(-1; j0), -
.
68
jV( )
0
-1
U( )
. 3.3.
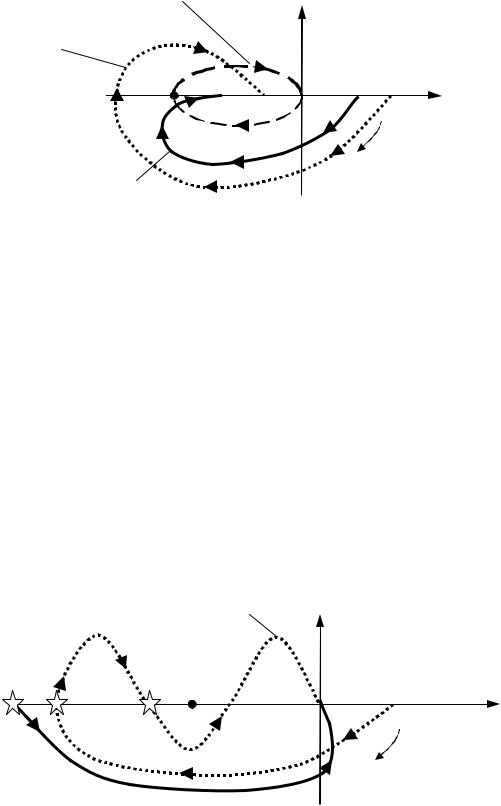
,
W( ) -
0 m/2
(-1; j0), m/2
+1 (-1; j0) ( . 3.4). +1 ,
– . = 0
W( ) -
+1 (-1; j0), , -
1/2 . m -
.
m = 0
jV( )
= 0 |
|
-1 |
0 |
= 0 |
|
(-1) |
(+1) |
U( ) |
|
(+1/2) |
|
|||
|
|
|
|
m = 1
. 3.4.
69
